cs231n神经网络

cs231n神经网络

单个神经元前向传播过程示例

class Neuron(object):
    #...
    def forward(self, inputs):
        """ assume inputs and weights are 1-D numpy arrays and bias is a number """
        cell_body_sum=np.sum(inputs*self.weights)+self.bias
        firing_rate=1.0/(1.0+math.exp(-cell_body_sum))   #sigmoid activation function
        return firing_rate

常用神经元激活函数

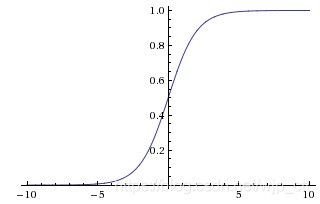
sigmoid

表达式$\sigma (x)=1/(1+e^{-x})$

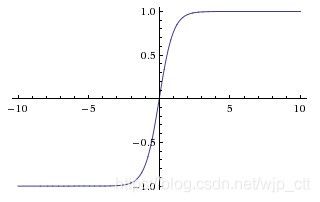
Tanh

表达式$\tanh (x)=2\sigma (2x)-1$

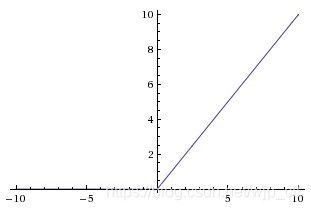
ReLU

表达式$f(x)=max(0,x)$

优势：加速收敛，计算简单

劣势：神经元可能永不被激活，“died”，可以通过合理设置学习率避免。

Leaky ReLU

表达式$f(x)=1(x<0)(\alpha x)+1(x>=0)(x)$，其中$\alpha$是一个很小的值

缺点是结果不恒定

Maxout

计算$max(w_1^T+b_1,w_2^T+b_2)$

Leaky ReLU是它的一种特殊形式

优势：具有ReLU单元的优点，但不会出现dying ReLU。

劣势：每个神经元具有双倍的参数。

网络结构

关于输出层

输出层通常不含有激活函数。这是因为最后一层通常用来表示每一类的socre（如分类任务），或者实数值（如回归任务）。

前向计算示例

#forward pass of a 3-layer neural network:
f =lamda x: 1.0/(1.0+np.exp(-x))      #activation function (use sigmoid)
x =np.random.randn(3,1)      #random input vector of three numbers
h1=f(np.dot(W1, x)+b1)       #first hidden layer
h2=f(np.dot(W2, h1)+b2)      #second hidden layer
out = np.dot (W3, h2)+b3     #output neuron

数据预处理

数据矩阵x，数据大小为N X D。

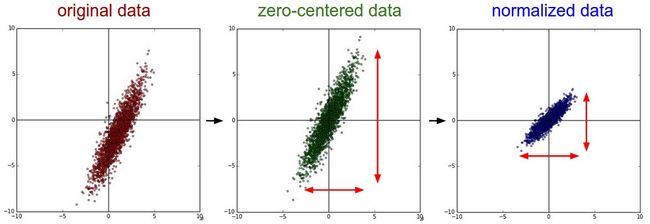
前去均值

X-=np.mean(X, axis=0)

对于图像数据，为了方便也可以所有像素减去一个单一值（或每个通道单独操作）

X-=np.mean(X)

标准化

目的：使每一维具有近似相同的尺度

• 法一：每一维除以标准差

X/=np.std(X, axis=0)

• 法二：预处理每一维使得该维度上的最小值和最大值分别是-1和1。

仅当不同的输入特征有不同的尺度，但使对于学习算法具有相同的重要性时才需要进行此操作。

对于图像而言，像素值在0到255之间，因此不一定要做标准化。

PCA和白化

计算协方差矩阵

#assume input data matrix X of size [NxD]
X-=np.mean(X, axis=0)  #zero-center the data
cov = np.dot(X.T, X)

协方差矩阵是对称半正定的，我们进行SVD分解。

U, S, V = np.linalg. svd(cov)

np.linalg.svd中，特征值是按照从小到大排列的。

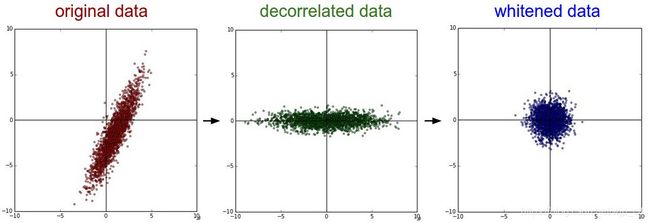
数据去相关

Xrot = np. dot(X , U)       #decorrelate the data

主成分分析（PCA）

Xrot_reduced = np.dot(X, U[:,:100])     #Xrot_reduced becomes [N x 100]

使用PCA可以节省时间和空间。

白化

得到的是零均值和单位协方差阵

#whiten the data
#divide by the eigenvalues(which are square roots of the singular values)
Xwhite =Xrot /np.sqrt(S+1e-5)

实际在卷积网络中，一般不使用PCA/白化，但常使用取均值结合标准化的操作。

预处理的数值（均值）只能在训练集上取，然后同时用于训练、验证和测试集上。

权重初始化

小的随机数

W=0.01*np.random.randn(D,H)来自于多维高斯的采样

用1/sqrt(n)修正方差

随机初始化的神经元的方差会随着输入数的增加而增加。

W=np.random.rand(n)/sqrt(n)，n是输入的数目。

对于ReLU神经元，推荐使用

W=np.random.rand(n)*sqrt(2.0/n)

初始化偏置

通常使用常数值，如0.01。

批量标准化

对初始值鲁棒

正则化

L2正则化

可以使网络使用所有的输入，而非多次使用部分输入

W + =-lamda*W

L1正则化

形式${\lambda }_1|w|+{\lambda }_2|W|$

L1正则化可以使权重向量在优化过程中变得稀疏。

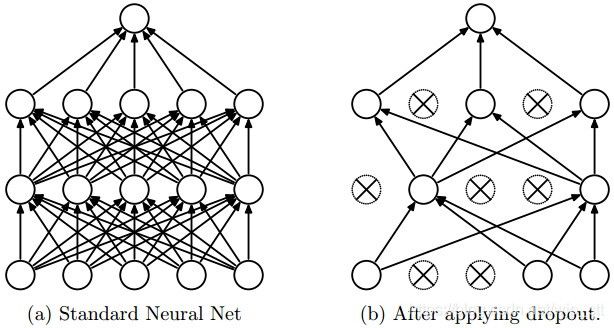
Dropout

在训练过程中一个神经元以概率p保持激活。

示例：

p=0.5     #probability of keeping a unit active

def train_step(X):
    """X contains the data"""
    #forward pass for example 3-layer neural network
    H1=np.maximum(0, np.dot(W1, X)+b1)
    U1=np.random.rand(*H1.shape)<p    #first dropout mask
    H1 *=U1 #drop!
    H2=np.maximum(0, np.dot(W2, H1)+b2)
    U2=np.random.rand(*H2.shape)<p    #second dropout mask
    H2 *=u2 #drop!
    out = np.dot(W3, H2)+b3
    
    #backward pass: compute gradients...
    #perform parameter update...
    
def predict(X):
	#ensembled forward pass
    H1=np.maximum(0, np.dot(W1, X)+b1)*p   #NOTE:scale the activations
    H2=np.maximum(0 ,np.dot(W2, H1)+ b2)*p  #NOTE:scale the activations
    out = np.dot(W3, H2)+b3

由于在测试时需要对激活进行按照p的尺度运算，我们通常使用inverted dropout。

p=0.5     #probability of keeping a unit active

def train_step(X):
    """X contains the data"""
    #forward pass for example 3-layer neural network
    H1=np.maximum(0, np.dot(W1, X)+b1)
    U1=(np.random.rand(*H1.shape)<p)/p    #first dropout mask. Notice /p!
    H1 *=U1 #drop!
    H2=np.maximum(0, np.dot(W2, H1)+b2)
    U2=(np.random.rand(*H2.shape)<p)/p    #second dropout mask. Notice /p!
    H2 *=u2 #drop!
    out = np.dot(W3, H2)+b3

	#backward pass: compute gradients...
	#perform parameter update...
 def predict(X):

	#ensembled forward pass
    H1=np.maximum(0, np.dot(W1, X)+b1)   #no scaling necessary
    H2=np.maximum(0 ,np.dot(W2, H1)+ b2)
    out = np.dot(W3, H2)+b3
   

通常使用经过交叉验证的全局的L2正则化项，也常和dropout结合。dropout的概率值默认设为0.5，也可以在测试集上进行调整。

损失函数

分类任务

• 使用svm损失函数

$$L_i=\sum _{j̸=y_i}max(0,f_j-f_{y_i}+1)$$

• 使用交叉熵的softmax

  $$L_i=-log(\frac{e^{f_{y_i}}}{\sum e_{f_j}})$$

当类别数很多时，使用Hierarchical Softmax

• 属性分类

$$L_i=\sum _{j̸=y_i}max(0,1-y_{ij}{f}_j)$$

其中$$y_{ij}$$的值为-1或+1，代表了第i个样本是否具有第j个属性。

另一种loss是对于每个属性训练一个logistic回归分类器，每一个二值化logistic分类器有两个值0和1，属于1的概率是
$$P(y=1|x;w,b)=\frac{1}{1+e^{-(w^{T}x+b)}}=\sigma (w^{T}x+b)$$
对数损失函数为
$$L_i=\sum _j{y}_{ij}log(\sigma (f_j))+(1-y_{ij})log(1-\sigma (f_j))$$

梯度检验

梯度检验是指比较比较分析梯度和数值梯度。

使用中心公式

$$\frac{df(x)}{dx}=\frac{f(x+h)-f(x-h)}{2h}$$

使用相对误差进行比较

$$\frac{|f_a^{{}^{\prime }}-f_n^{{}^{\prime }}|}{max(|f_a^{{}^{\prime }}|,|f_n^{{}^{\prime }}|)}$$

最佳的结果范围是小于等于1e-7.

网络更深，相对误差就更大。对于一个10层的网络，相对误差为1e-2就可以了。

使用double精度

围绕浮点活动范围

目标中的不可微部分

如ReLU，SVM损失，maxout神经元等。如对于x<0的点，ReLU的导数等于0，但f(x+h)可能越过不可微点。

仅使用少量数据点

解决以上问题的方法是使用更少的数据点。使用更少的数据点，则会遇到更少的不可微点。如果你仅check2~3个数据点，你几乎可以check整个batch。

谨慎选择step的长度h

h并不一定是越小越好，因为当h很小的时候，你会遇到数值精度问题。有时当梯度不能通过检验时，通过将h改为1e-4或1e-6会突然通过检验。

不要让正则项压倒数据

推荐首先去掉正则项并单独检验数据损失，然后单独检验正则项。

关闭dropout或数据增强

记得去掉网络中任何非确定性的因素，如dropout、随机数据增强等。

最好在计算f(x+h)和f(x-h)以及数值梯度之前，固定一个特定的随机种子。

只检验少数维度

通常梯度检验会面临百万级的参数。一种实际的检验方法是只检验部分维度的梯度并假设剩余的是正确的。

在特征模式中进行梯度检验

使用一个内置时间，在损失开始下降后，网络被允许进行学习和进行梯度检验。在第一次迭代进行梯度检验可能会引入梯度的错误计算。

训练前进行完整性检查

寻找正确的损失

在初始化后检查数据损失（将正则项设置为0）。

如10类的sotfmax期望损失为2.302，因为-ln(0.1)=2.302。

10类的svm损失函数，期望损失为9，因为socres接近0，所有的margin都不会满足。

过拟合数据的一个小子集

在整个数据集上训练之前在一个小的子集（如20个样本）上进行训练并确保loss可以降到0。

跟踪学习过程

plot的x轴都是以epochs为单位的，表示在训练过程中一个样本被使用次数的期望。我们更常用的是跟踪epoch而不是iteration，因为iteration的数目取决于batch大小的设置。

损失函数

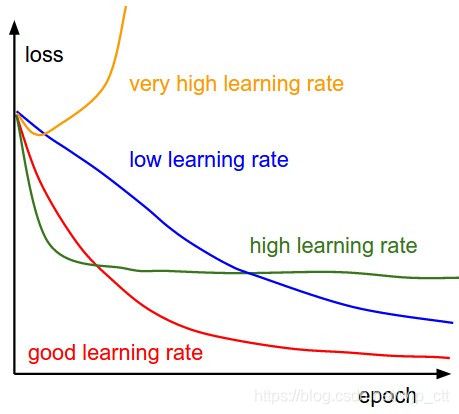
不同的learning rate对应的loss曲线。

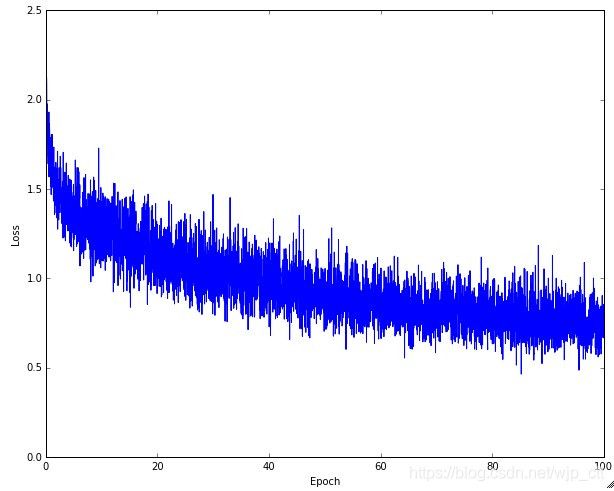
典型的loss曲线，这里噪声大的原因是batch的大小较小。

训练/验证精度

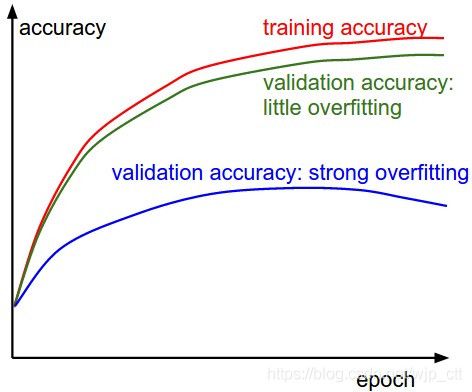
在训练过程中另一个需要跟踪的量是训练/验证精度

对于验证精度，有两种情况。蓝线表示强过拟合，说明需要提高正则项（更高的L2权重惩罚，更多的dropout）或者收集更多数据。另一种情况是验证精度能较好地跟踪训练精度。这表明模型的容量不是足够大：通过增加参数数目提升模型的容量。

权重比：更新

最后一项需要跟踪的量是更新大小和值大小的比例。这个比率的粗略启发式值是1e-3，如果比率比这个值低，说明学习率过低，否则说明学习率过高。

#assume parameter vector W and its gradient vector dW
param_scale = np.linalg.norm(W.ravel())
update = -learning_rate*dW   #simple SGD update
update_scale = np.linalg.norm(update.ravel())
W += update   #the actual update
print (update_scale/param_scale)   #want ~1e-3

第一层可视化

第二张图是好的权重图。第一张具有噪声，意味着：未收敛的网络、不正确的学习率，低的权重正则项惩罚。

参数更新

Vanllia update

最简单的参数更新方式，沿着负梯度方向更新

#Vanilla update
x += -learning_rate*dx

动量更新

#Momentum update
v = mu*v -learning_rate*dx
x += v    #integrate position

超参数mu为动量（常用值为0.9）。

一种典型的处理动量的方法是从0.5开始并在几个epoch之后将其退火到0.99。

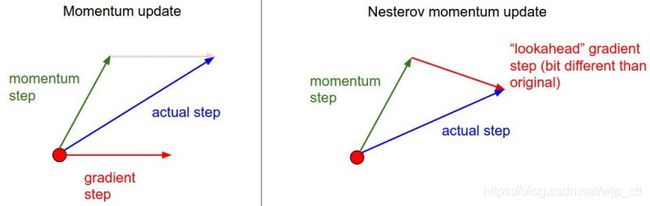
Nesterov动量

效果比标准动量法略好。

“提前看”的想法。计算在x + mu*v的梯度而不是在x的梯度。

x_ahead = x + mu*v
#evaluate dx_ahead (the gradient at x_ahead instead of at x)
v = mu * v - learning_rate *dx_ahead
x += v

与SGD或标准动量更新形式上保持一致

v_prev = v    # back this up
v = mu * v -learning_rate * dx
x += -mu *v_prev + (1 + mu) * v

学习率退火

step decay

例如每5个epoch将学习率减半，或者每20个epoch将学习率变为原来的1/10。取决于问题和模型。一种启发式方法是观察在固定学习率下的验证误差，当验证误差不再下降时降低学习率。

exponential decay
$$\alpha ={\alpha }_0{e}^{-kt}$$
1/t decay
$$\alpha ={\alpha }_0/(1+kt)$$

各参数自适应学习率方法

Adagrad

#Assume the gradient dx and parameter vector x
cache += dx**2
x += - learning_rate * dx /(np.sqrt(cache)+eps)

cache的size与梯度相同，平滑项eps（大小通常在1e-4到1e-8之间）避免了除0。

RMSprop

使用了梯度平方的滑动平均

cache= decay_rate * cache +(1-decay_rate) * dx **2
x += -learning_rate *dx/(np.sqrt(cache)+eps)

这里的decay_rate是超参数并且典型值为[0.9, 0.99, 0.999]

Adam

Adam像具有动量的RMSProp法：

m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m /(np.sqrt(v)+eps)

这里使用了平滑的梯度m取代了原始梯度dx。推荐的参数值为eps=1e-8,beta1=0.9,beta2=0.999。

Adam现在通常用为默认的算法并且比RMSProp效果略好。

完整的Adam更新算法包括偏差校正机制。该机制弥补了该问题：在最初的几步中，向量m,v在它们完全被“预热”前都被初始化并且偏执为0。

# t is your iteration counter going from 1 to infinity
m = beta1*m +(1-beta1)*dx
mt = m/(1-beta1**t)
v = beta2*v +(1-beta2)*(dx**2)
vt = v / (1-beta2**t)
x += - learning_rate * mt/(np.sqrt(vt)+eps)

超参数优化

神经网络中最常见的超参数为：

• 初始学习率
• 学习率下降方式
• 正则化强度（L2惩罚项，dropout强度）

实施计划

使用一个叫做工人的程序，让工人连续次啊杨随机超参数并执行优化。在训练期间，工人在每个epoch后跟踪新能，并将checkpoint写入模型，这样检查和排序进度很简单。第二个叫主人的程序，负责启动或杀死工人，检查工人写入的checkpoint并绘制统计数据。

首选一个验证集进行交叉验证

超参数范围

超参数的典型采样范围是learning_rate = 10 ** uniform(-6, 1)。对于正则化强度，使用相同的策略。

使用随机搜索代替网格搜索

小心再边界上的最优值

例如，我们使用learning_rate = 10 ** uniform(-6, 1)。当我们得到结果后，我们应当再次检验最终的学习率不在边界上。

从粗略搜索到精细搜索

评估

模型融合

训练许多独立的模型，在测试阶段求预测的平均值。以下是形成融合的一些方法：

• 相同的模型，不同的初始化
• 在交叉验证中发现的最优模型
• 单一模型，不同的checkpoint。缺点是缺乏多样性，但在实践中仍能很好地工作。优点是不产生额外计算
• 训练中参数的平均。目标是碗形的，训练中网络在模式中跳跃，使用平均值更有可能获得接近模式的地方。

总结

训练一个神经网络，需要注意：

• 使用小的batch进行梯度检验。

• 确保初始损失合理，可以在数据的一个小的子集上获得100%训练准确率。

• 两种推荐的更新算法是SGD+Nesterov Momentum或Adam

• 在训练过程中降低学习率。

• 使用随机搜索寻找好的超参数。从粗略搜索到精细搜索

• 使用模型融合提升性能。