学习超大神经网络,CPU超越V100 GPU,靠的居然是哈希?
机器之心报道
机器之心编辑部
训练一亿参数量的全连接网络,44 核心 CPU 让 V100 甘拜下风,靠的居然是——哈希?
深度学习模型的训练和推理加速近来是研究领域关注的重点。虽然普遍观点认为,GPU 相比 CPU 有更强的算力优势。但在近日,莱斯大学的计算机科学家们公布了新的研究成果,其提出的深度学习框架,在大型工业级的推荐数据集上验证了在没有类似于 GPU 的专业硬件加速条件下,也可以对深度学习进行加速。
在论文中,研究者指出,尽管已有的研究表明,在算法端对模型进行优化无法显示出如同 V100 GPU 那样强大的性能提升,但是他们提出的 SLIDE 引擎却可以实现。这一模型可以显著地减少训练和推理阶段的运算,比在 GPU 上 经过 TensorFlow 高度优化过的算法还要快。
例如,在工业级的推荐数据集上测试 SLIDE 时,Tesla V100 GPU 上的训练时间是 Intel Xeon E5-2699A 2.4GHZ 的 3.5 倍。而在同样的 CPU 硬件条件下,SLIDE 比 TensorFlow 快了 10 倍。
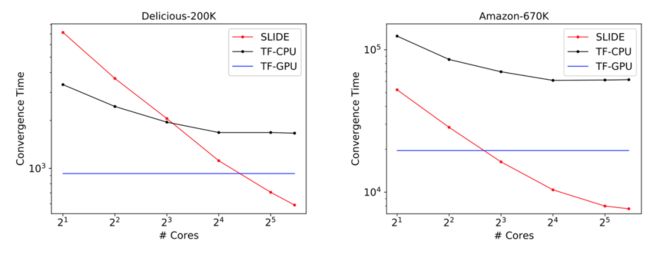
我们可以先看张实验图,在 Amazon-670K 这样的复杂分类数据集上,超一亿参数量的大型神经网络训练时间竟然是 SLIDE + CPU 最快,连 TensorFlow + Tesla V100 都要慢很多。而且从迭代步数上看,它们两者是等价的,表明模型的收敛行为是相同的。
![]()
对于论文和结果的复现,研究者已提供了相应的代码。
论文链接:https://www.cs.rice.edu/~as143/Papers/SLIDE_MLSys.pdf
开源地址:https://github.com/keroro824/HashingDeepLearning
计算复杂度大降,局部敏感哈希立功
如此神奇的加速是怎么实现的?具体而言,研究者采用了局部敏感哈希(Locality Sensitive Hashing)算法,并在神经网络中使用了自适应 dropout。局部敏感哈希是一类哈希算法,当输入数据彼此类似的时候,具有更高的碰撞概率,而不相似的算法彼此碰撞的概率很低。一种广泛应用的最近邻逼近搜索算法就使用了局部敏感哈希理论。
SLIDE 的局部敏感哈希如何构建
在 Indyk 和 Motwani 在 1998 年的一项研究中表明,对于给定的相似性计算,一类 LSH 函数就足以有效地解决次线性时间中的最近相邻搜索。
算法:LSH 算法使用两个参数(K,L),研究者构造了 L 个独立的哈希列表。每个哈希表都有一个原始哈希函数 H,而该函数是由集合 F 里 K 个随机的独立哈希函数串联而成。在给定一个查询下,从每一个哈希列表中采集一个 bucket 后会返还 L 个 bucket 的集合。
直观地说,原哈希函数使得 bucket 变得稀疏,并减少了误报的数量,因为只有有效的最近相邻项才可以匹配给所查询的所有 K 的哈希值。L 的 bucket 集合通过增加可存放的最近相邻项的潜在 bucket 数量来减少漏报的数量。而候选生成算法分为两个阶段工作:
1. 预处理阶段,通过储存所有 x 元素,从数据层面构造 L 的哈希列表。只存储哈希列表中指向向量的指针,因为储存整个数据向量会非常低效。
2. 查询阶段:给定一个查询 Q,搜索其最近相邻项,从 L 的哈希列表所收集的所有 bucket 集合进行报告。这里注意,不需要去扫描所有的元素,只是在探测 L 的不同的 bucket,而每个哈希列表里都有一个 bucket。
在生成潜在的候选算法后,通过比较候选集里的每个子项与查询间的距离从而计算处最近相邻项。
将局部敏感哈希用于采样和预估
虽然局部敏感哈希被证明能够在亚线性条件下进行快速抽取,但是对于精确搜索而言速度非常慢,因为它需要大量的哈希表。有研究表明,通过如图 1 所示的高效采样能够在一定程度上缓解搜索的计算量,只需要看一些哈希桶就能够做到足够的自适应采样。
图 1:局部敏感哈希的图示。对于一个输入,可以从对应的哈希桶中抽取哈希码。
而最近在最大化内积搜索(maximum inner product search:MIPS)的研究也说明了这一点,在这里,可以使用非对称局部敏感哈希,使得采样大的内积变得可能。给定一个向量集合 C 和查询向量 Q。使用 (K,L)--参数化的 LSH 算法和 MIPS 哈希,可以获得一个候选集合 S。在这里,只需要一次线性成本,对 C 进行哈希化的预处理,而对于 Q 则只需要少量哈希查表工作。
SLIDE 中的算法,包括框架(算法 1)和哈希采样(算法 2)。
构建 SLIDE 系统
图 2:SLIDE 系统架构。
在 SLIDE 架构中,其核心模块是网络。该神经网络由一些单层模块组成。对于每个层的模块,其都是由神经元和一些哈希表组成——即将神经元的 ids 转换成哈希。
对于每个神经元来说,它都有多个批大小长度数组:1)一个二元数组,表示对于每个输入,该神经元是否激活;2)每个输入的激活;3)批数据中每个输入的累积梯度;4)该层和上一层连接权重;5)上一层神经元数量,由最后一个数组表示。
初始化
每层对象包含一个神经元列表以及一组 LSH 采样哈希列表。每个哈希列表包含被散列至 bucket 中神经元的 ids。在网络初始化过程中,网络的权重值是随机初始化的。随后,对每层使用 L 的哈希列表进行初始化 K * L LSH 函数。
使用哈希表采样进行稀疏前向传播
在前向传播阶段,给定一个单独的训练实例,研究者会计算直到最后一层的网络激活,并给出输出。在 SLIDE 中,他们不会去计算每层的所有激活,而是将每层的输入 xl 输入到哈希函数中,得到 hl(xl),哈希码作为查询,从对应匹配的 buckets 中获得激活(采样)的神经元的 ids。
稀疏反向传播/梯度更新
反向传播步骤紧接着前向传播进行。计算了神经网络的输出之后,研究者会将输出和标签进行比较,并将误差逐层进行反向传播,来计算梯度、更新权重。这里他们使用了经典的反向传播方法。
权重更新后再更新哈希列表
权重值更新后,需要相应地调整哈希列表中神经元的位置。更新神经元通常涉及到从旧的哈希桶中删除,然后再从新的哈希桶中添加新的内容,这可能会非常耗时。在 4.2 节中,将讨论几种用于优化更新哈希列表所导致昂贵开销的设计技巧。
OpenMP 跨批量处理的并行化
对于任何给定的训练实例中,前馈以及反向传播操作都是按照顺序的,因为它们需要逐层的去执行。SLIDE 使用常用的批量处理梯度的下降方法以及 Adam 优化器,批量处理大小通常在几百个左右。批量处理中的每个数据实例的运行都在单独的线程中,其梯度是按照并行方式计算的。
梯度更新的极端稀疏性以及随机性使得我们可以在不导致大量重叠更新的情况下,在不同的训练数据上通过异步并行处理梯度累积的步骤。SLID 大量地使用了 HOGWILD 的理论 (Recht et al., 2011),同时也表明少量的重叠是可控的。
真 → CPU 比 GPU 快
研究者在论文后面附上了一系列实验结果,包括对比采用 Tesla V100 GPU 的 TensorFlow 模型、对比采用 两个 Intel Xeon E5-2699A CPU(单个 22 核心,总共 44 核心)的 TensorFlow 模型,对比 SLIDE 自适应采样与带采样的 Softmax 之间的性能等等。我们可以发现,SLIDE 在 CPU 上的训练速度,竟然惊人地高效。
首先对于测试模型,研究者采用了具有一亿参数量的超大全连接模型,数据集也是 Delicious200K 和 Amazon-670K 这种大型工业级分类数据集。这两个数据集分别有 78 万+和 13 万+特征维度,20 万+和 67 万+的类别数量,看着就恐怖。因为特征维度和分类类别太高,即使隐藏层单元不多,整体的参数量也会剧增。
如下图所示展示了论文的主要结果,CPU 上的 SLIDE 从时间上要比 V100 快(采用 TensorFlow 框架),且能一直优于基于 CPU 的 TF 模型。
图 5:SLIDE(红线)、TF-GPU(蓝线)和 TF-CPU(黑线)之间的效果对比。
在 Delicious200K 数据集上,SLIDE 比 TF-GPU 快 1.8 倍。而在需要更大算力的 Amazon-670K 上,TF-GPU 的收敛时间是 SLIDE 的 2.7 倍(2 小时与 5.5 小时)。从迭代量来看,两者之间的收敛行为也是等价的,只不过每一次迭代 SLIDE 都快一些。
此外,在图 5 中,最后的收敛效果都是差不多的,也就是说在 SLIDE 框架下,模型效果并不会被破坏。
表 2 展示了 CPU 核心的使用情况,其分别测试了框架在使用 8、16、32 线程下的负载情况。我们可以看到,对于 TF-CPU,其使用率非常低(<50%),且随着线程的增加,使用率会进一步降低。对于 SLIDE,计算核心的利用是非常稳定的,大约在 80% 左右。
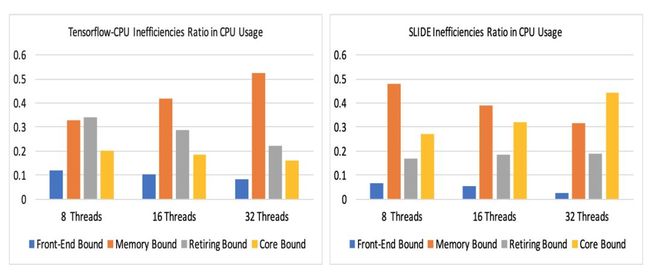
图 6 展示了 TF-CPU 和 SLIDE 在 CPU 无效利用率上的分布情况。SLIDE 对于计算核心的利用率要远远高于 TF-CPU 的利用率。
图 6:CPU 低效利用率:Memory-bound 的低效利用率(橙色)对于这两种算法是最显著的。TF-CPU 随着核心数的增加,Memory-bound 低效利用率也会增加,而 SLIDE 会降低。
因为能高效利用 CPU 的计算资源,SLIDE 随着 CPU 核心数的 增加,收敛时间还能极大地降低。
图 9:TF-CPU 与 SLIDE 之间的可扩展性测试,很明显 SLIDE 要强很多。
代码示例
现在 SLIDE 已经开源。在开源项目中,作者提供了数据集和相应的代码进行测试。
首先,使用者需要安装 CNPY,并开启 Transparent Huge Pages,SLIDE 需要大约 900 个 pages,每个 2MB,以及 10 个 1GB 的 pages。
运行代码过程如下:
make
./runme Config_amz.csv
需要注意的是,Makefile 需要基于 CNPY 修改路径,同时需要修改的包括在 Config_amz.csv 中的 trainData、testData、logFile 等。
至于训练数据,它来自 Amazon-670K ,下载地址如下:
https://drive.google.com/open?id=0B3lPMIHmG6vGdUJwRzltS1dvUVk
在工业领域中,模型结构并不一定非常复杂,朴素贝叶斯、全连接网络这些简单模型往往能获得更多的青睐。然而,真实模型通常非常庞大,配置高性能 GPU 来训练模型非常不划算。即使这篇论文只验证了全连接网络,但至少说明高性能 CPU 真的能满足大模型的训练,能大量降低硬件成本。
![]()