计算机图形学：贝塞尔曲线和B样条

贝塞尔曲线和B样条

1.Bézier curve贝塞尔曲线

一个连续函数都可以用一个多项式无限逼近

贝塞尔曲线于 1962 年，由法国工程师皮埃尔·贝济埃（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。

1.1 一阶贝塞尔曲线

$${\mathbf{B}}_1(\mathbf{t})=(1-\mathbf{t}){\mathbf{P}}_0+\mathbf{t}{\mathbf{P}}_1,\mathbf{t}\in [0,1]$$

1.2 二阶贝塞尔曲线

$$\begin{gathered} {\mathbf{P}}_0^{\prime }=(1-\mathbf{t}){\mathbf{P}}_0+\mathbf{t}{\mathbf{P}}_1 \\ {\mathbf{P}}_1^{\prime }=(1-\mathbf{t}){\mathbf{P}}_1+\mathbf{t}{\mathbf{P}}_2 \\ {\mathbf{B}}_2(\mathbf{t})=(1-\mathbf{t}){\mathbf{P}}_0^{\prime }+\mathbf{t}{\mathbf{P}}_1^{\prime }=(1-\mathbf{t}{)}^2{\mathbf{P}}_0+2\mathbf{t}(1-\mathbf{t}){\mathbf{P}}_1+{\mathbf{t}}^2{\mathbf{P}}_2 \end{gathered}$$

1.3 三阶贝塞尔曲线

$${\mathbf{B}}_3(\mathbf{t})=(1-\mathbf{t}{)}^3{\mathbf{P}}_0+3\mathbf{t}(1-\mathbf{t}{)}^2{\mathbf{P}}_1+3{\mathbf{t}}^2(1-\mathbf{t}{)}^2{\mathbf{P}}_1+{\mathbf{t}}^3{\mathbf{P}}_3$$

1.4 多阶贝塞尔曲线

Bernstein polynomial(伯恩斯坦多项式)

$$\begin{gathered} {\mathbf{B}}_{\mathbf{n}}(\mathbf{t})=\sum _{\mathbf{i}=0}^{\mathbf{n}}{\mathbf{C}}_{\mathbf{n}}^{\mathbf{i}}{\mathbf{P}}_{\mathbf{i}}(1-\mathbf{t}{)}^{\mathbf{n}-\mathbf{i}}{\mathbf{t}}^{\mathbf{i}}=\sum _{\mathbf{i}=0}^{\mathbf{n}}{\mathbf{B}}_{\mathbf{i},\mathbf{n}}{\mathbf{P}}_{\mathbf{i}} \\ {\mathbf{C}}_{\mathbf{n}}^{\mathbf{i}}=\frac{\mathbf{n}!}{(\mathbf{n}-\mathbf{i})!\cdot \mathbf{i}!} \\ {\mathbf{B}}_{\mathbf{i},\mathbf{n}}=\frac{\mathbf{n}!}{(\mathbf{n}-\mathbf{i})!\cdot \mathbf{i}!}(1-\mathbf{t}{)}^{\mathbf{n}-\mathbf{i}}{\mathbf{t}}^{\mathbf{i}} \end{gathered}$$

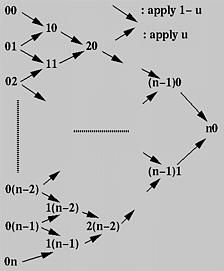
1.5 de Casteljau

${\mathbf{P}}_{\mathbf{i},\mathbf{j}}$表示第i列的第j个点
$$\begin{gathered} {\mathbf{P}}_{\mathbf{i},\mathbf{j}}=(1-\mathbf{t}){\mathbf{P}}_{\mathbf{i}-1,\mathbf{j}}+\mathbf{t}{\mathbf{P}}_{\mathbf{i}-1,\mathbf{j}+1} \\ \mathbf{i}\in [1,\mathbf{n}],\mathbf{j}\in [1,\mathbf{n}-\mathbf{i}+1] \end{gathered}$$

de Casteljau算法在Bézier曲线的光栅化阶段特别有用。

Vector2 Render::CalculateBezierPoint(const std::vector<Vector2>& ctl_vecs, float t){
    std::vector<Vector2> points(ctl_vecs);
    for (int i = 0; i < points.size() - 1; ++i) {
        for (int j = 0; j < points.size() - i - 1; ++j) {
            points[j] = interp(points[j], points[j + 1], t);
        }
    }
    return points[0];
}

1.6 升阶

增加控制点却不改变原先曲线的表现

Degree raising means that adding control points to raise the degree of the Bézier curves, but the shape and direction of the curve remain unchanged.

推导过程：

已知：
$${\mathbf{B}}_{\mathbf{n}}(\mathbf{t})=\sum _{\mathbf{i}=0}^{\mathbf{n}}{\mathbf{B}}_{\mathbf{i},\mathbf{n}}{\mathbf{P}}_{\mathbf{i}}$$
则：
$${\mathbf{B}}_{\mathbf{n}}(\mathbf{t})=\sum _{\mathbf{i}=0}^{\mathbf{n}}{\mathbf{B}}_{\mathbf{i},\mathbf{n}}{\mathbf{P}}_{\mathbf{i}}=\sum _{\mathbf{i}=0}^{\mathbf{n}}(1-\mathbf{t}+\mathbf{t}){\mathbf{B}}_{\mathbf{i},\mathbf{n}}{\mathbf{P}}_{\mathbf{i}}$$

接下来看下相乘的两个式子

式子1:

$$\begin{gathered} (1-\mathbf{t}){\mathbf{B}}_{\mathbf{i},\mathbf{n}}{\mathbf{P}}_{\mathbf{i}}=\frac{\mathbf{n}!}{(\mathbf{n}-\mathbf{i})!\cdot \mathbf{i}!}(1-\mathbf{t}{)}^{\mathbf{n}+1-\mathbf{i}}{\mathbf{t}}^{\mathbf{i}}{\mathbf{P}}_{\mathbf{i}} \\ =\frac{\mathbf{n}+1-\mathbf{i}}{\mathbf{n}+1}\frac{(\mathbf{n}+1)!}{(\mathbf{n}+1-\mathbf{i})!\cdot \mathbf{i}!}(1-\mathbf{t}{)}^{\mathbf{n}+1-\mathbf{i}}{\mathbf{t}}^{\mathbf{i}}{\mathbf{P}}_{\mathbf{i}}=\frac{\mathbf{n}+1-\mathbf{i}}{\mathbf{n}+1}{\mathbf{B}}_{\mathbf{i},\mathbf{n}+1}{\mathbf{P}}_{\mathbf{i}} \\ (1-\mathbf{t}){\mathbf{B}}_{\mathbf{i},\mathbf{n}}{\mathbf{P}}_{\mathbf{i}}=\frac{\mathbf{n}+1-\mathbf{i}}{\mathbf{n}+1}{\mathbf{B}}_{\mathbf{i},\mathbf{n}+1}{\mathbf{P}}_{\mathbf{i}} \end{gathered}$$

式子2:

$$\begin{gathered} \mathbf{t}{\mathbf{B}}_{\mathbf{i},\mathbf{n}}{\mathbf{P}}_{\mathbf{i}}=\frac{\mathbf{n}!}{(\mathbf{n}-\mathbf{i})!\cdot \mathbf{i}!}(1-\mathbf{t}{)}^{\mathbf{n}-\mathbf{i}}{\mathbf{t}}^{\mathbf{i}+1}{\mathbf{P}}_{\mathbf{i}} \\ =\frac{\mathbf{i}+1}{\mathbf{n}+1}\frac{(\mathbf{n}+1)!}{(\mathbf{n}+1-\mathbf{i}-1)!\cdot (\mathbf{i}+1)!}(1-\mathbf{t}{)}^{\mathbf{n}+1-\mathbf{i}-1}{\mathbf{t}}^{\mathbf{i}+1}{\mathbf{P}}_{\mathbf{i}}=\frac{\mathbf{i}+1}{\mathbf{n}+1}{\mathbf{B}}_{\mathbf{i}+1,\mathbf{n}+1}{\mathbf{P}}_{\mathbf{i}} \\ \mathbf{t}{\mathbf{B}}_{\mathbf{i},\mathbf{n}}{\mathbf{P}}_{\mathbf{i}}=\frac{\mathbf{i}+1}{\mathbf{n}+1}{\mathbf{B}}_{\mathbf{i}+1,\mathbf{n}+1}{\mathbf{P}}_{\mathbf{i}} \end{gathered}$$

对于等式1，由于i = n + 1的时候等式为0，所以可以将等式变为

$$\sum _{\mathbf{i}=0}^{\mathbf{n}}\frac{\mathbf{n}+1-\mathbf{i}}{\mathbf{n}+1}{\mathbf{B}}_{\mathbf{i},\mathbf{n}+1}{\mathbf{P}}_{\mathbf{i}}=\sum _{\mathbf{i}=0}^{\mathbf{n}+1}\frac{\mathbf{n}+1-\mathbf{i}}{\mathbf{n}+1}{\mathbf{B}}_{\mathbf{i},\mathbf{n}+1}{\mathbf{P}}_{\mathbf{i}}$$

对于等式2我们可以将i用i-1替代，因为i=-1时等式为0，所以成立，所以

$$\sum _{\mathbf{i}=0}^{\mathbf{n}}\frac{\mathbf{i}+1}{\mathbf{n}+1}{\mathbf{B}}_{\mathbf{i}+1,\mathbf{n}+1}{\mathbf{P}}_{\mathbf{i}}=\sum _{\mathbf{i}=0}^{\mathbf{n}+1}\frac{\mathbf{i}}{\mathbf{n}+1}{\mathbf{B}}_{\mathbf{i},\mathbf{n}+1}{\mathbf{P}}_{\mathbf{i}-1}$$

将两式子合并最终结果为：

$${\mathbf{B}}_{\mathbf{n}}(\mathbf{t})=\sum _{\mathbf{i}=0}^{\mathbf{n}}{\mathbf{B}}_{\mathbf{i},\mathbf{n}}{\mathbf{P}}_{\mathbf{i}}=\sum _{\mathbf{i}=0}^{\mathbf{n}+1}(\frac{\mathbf{n}+1-\mathbf{i}}{\mathbf{n}+1}{\mathbf{P}}_{\mathbf{i}}+\frac{\mathbf{i}}{\mathbf{n}+1}{\mathbf{P}}_{\mathbf{i}-1}){\mathbf{B}}_{\mathbf{i},\mathbf{n}+1}$$

其中${\mathbf{P}}_{-1},{\mathbf{P}}_{\mathbf{n}+1}$值随意，毕竟最后乘以系数后均为0

新的节点推导公式为：
$${\mathbf{P}}_{\mathbf{i}}^{\ast }=(\frac{\mathbf{n}+1-\mathbf{i}}{\mathbf{n}+1}{\mathbf{P}}_{\mathbf{i}}+\frac{\mathbf{i}}{\mathbf{n}+1}{\mathbf{P}}_{\mathbf{i}-1})$$

CODE:

std::vector<Vector2> Render::RaiseDegree(const std::vector<Vector2>& ctl_vecs){
    unsigned long new_degree = ctl_vecs.size();
    std::vector<Vector2> new_ctl_vecs(new_degree + 1);
    new_ctl_vecs[0] = ctl_vecs[0];
    new_ctl_vecs[new_degree] = ctl_vecs[new_degree - 1];
    for (int i = 1; i < new_degree; ++i) {
        float t = 1.0 - static_cast<float>(i) / new_degree;
        new_ctl_vecs[i] = interp(ctl_vecs[i - 1], ctl_vecs[i], t);
    }
    return new_ctl_vecs;
}

1.7 降阶

减少控制点去逼近原先曲线的表现

Degree reduction is the opposite of degree raising, is to find a curve defined by new control points with minimum error

根据升阶公式

$${\mathbf{P}}_{\mathbf{i}}^{\ast }=(\frac{\mathbf{n}-\mathbf{i}}{\mathbf{n}}{\mathbf{P}}_{\mathbf{i}}+\frac{\mathbf{i}}{\mathbf{n}}{\mathbf{P}}_{\mathbf{i}-1})$$

可以得到如下两个递推式

$$\begin{gathered} {\mathbf{P}}_{\mathbf{i}}^{\prime }=\frac{\mathbf{n}{\mathbf{P}}_{\mathbf{i}}^{\ast }-\mathbf{i}{\mathbf{P}}_{\mathbf{i}-1}^{\prime }}{\mathbf{n}-\mathbf{i}}\mathbf{i}=0,1,2...\mathbf{n}-1 \\ {\mathbf{P}}_{\mathbf{i}-1}^{\prime \prime }=\frac{\mathbf{n}{\mathbf{P}}_{\mathbf{i}}^{\ast }-(\mathbf{n}-\mathbf{i}){\mathbf{P}}_{\mathbf{i}}^{\prime \prime }}{\mathbf{i}}\mathbf{i}=\mathbf{n},\mathbf{n}-1,...1 \end{gathered}$$

一个与起点重合，然后逐渐偏离；一个与终点重合，然后逐渐偏离

Then we have two kinds of degree reduction schemes

1.7.1 Forrest (1972)

$$\widehat{{\mathbf{P}}_{\mathbf{i}}}=\{\begin{array}{cc}{P}_i^{\prime },& i=0,1,...,\left[\frac{n-1}{2}\right]\\ P_i^{\prime \prime },& i=\left[\frac{n-1}{2}\right]+1,...n-1\end{array}$$

1.7.2 Farin (1983)

$$\widehat{{\mathbf{P}}_{\mathbf{i}}}=(1-\frac{\mathbf{i}}{\mathbf{n}-1}){\mathbf{P}}_{\mathbf{i}}^{\prime }+\frac{\mathbf{i}}{\mathbf{n}-1}{\mathbf{P}}_{\mathbf{i}}^{\prime \prime }$$

---

2 B-Spline

$$\begin{gathered} P_n(t)=\sum _{i=0}^n{P}_i{N}_{i,k}(t) \\ t\in [0,1] \end{gathered}$$

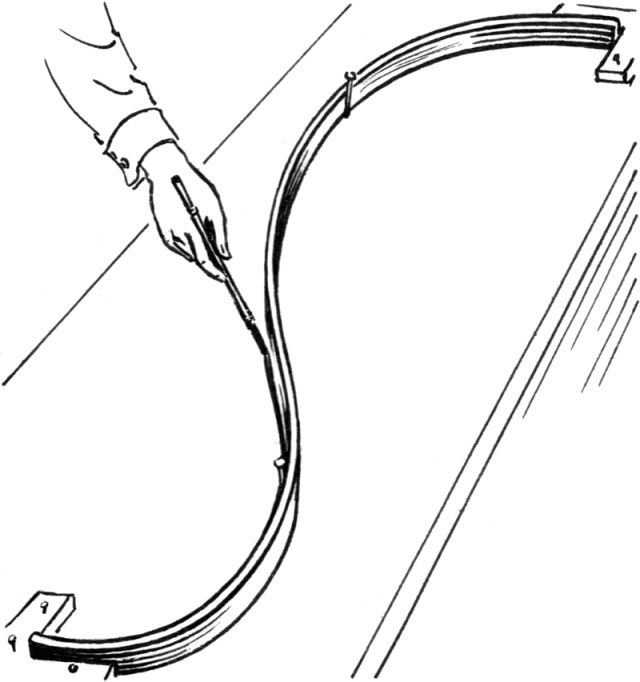
2.1 样条

样条（Spline）其实是一种在造船和工程制图时用来画出光滑形状的工具。样条是一根柔软但有弹性的长条物，有些像尺子。将两端和几个点用钉子固定之后，便可以产生顺滑的曲线。

2.2 Cox-de Boor recursion formula

$$\begin{gathered} {\mathbf{N}}_{\mathbf{i},1}=\{\begin{array}{cc}1& t_i<x<t_{i+1}\\ 0& otherwise\end{array} \\ {\mathbf{N}}_{\mathbf{i},\mathbf{k}}=\frac{\mathbf{t}-{\mathbf{t}}_{\mathbf{i}}}{{\mathbf{t}}_{\mathbf{i}+\mathbf{k}-1}-{\mathbf{t}}_{\mathbf{i}}}{\mathbf{N}}_{\mathbf{i},\mathbf{k}-1}(\mathbf{t})+\frac{{\mathbf{t}}_{\mathbf{i}+\mathbf{k}}-\mathbf{t}}{{\mathbf{t}}_{\mathbf{i}+\mathbf{k}}-{\mathbf{t}}_{\mathbf{i}+1}}{\mathbf{N}}_{\mathbf{i}+1,\mathbf{k}-1}(\mathbf{t}) \end{gathered}$$

我们让$t_0=0,t_1=1,t_2=2,t_3=3$,则$N_{0,1},N_{1,1},N_{2,1}$如下图所示：

递推关系如下（此图为wiki上的，用的是次-degree，而上面的公式用的是阶-order，degree=order-1）：

2.2.1 定义区间

$[t_{k-1},t_{n+1}]$区间内有相应数量的基函数，该区间才有意义：

2.3 分类

2.3.1 均匀B样条（Uniform B-Spline）

节点成等差数列均匀分布

2.3.2 准均匀B样条（Quasi-Uniform B-Spline）

让起点和终点都具有K的重复度，使得曲线从起点开始，到终点结束

2.3.3 分段Bezier曲线(Piecewise Bezier Curve)

• 起点节点和终点节点都具有K的重复度
• 所有其它节点都具有K-1的重复度
• 这样所有的曲线段都是Bezier曲线，各自独立

2.3.4 非均匀B样条（Non-uniform B-Spline）

• 起始点重复度都≤K
• 其它节点重复度≤K-1

De Boor’s Algorithm