7.8训练
A题
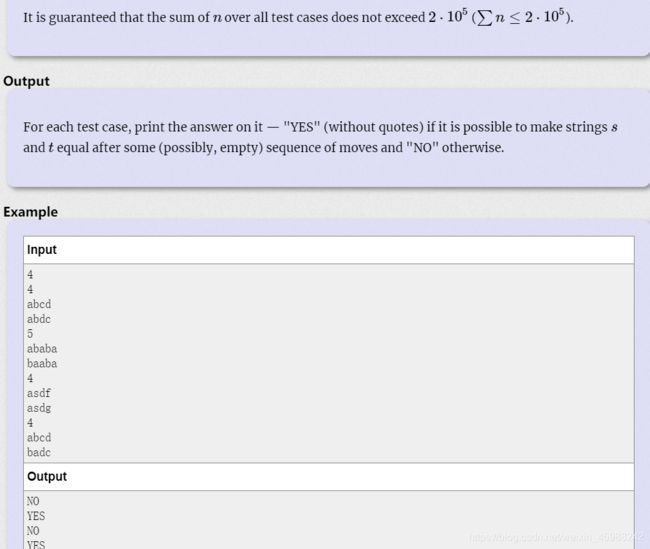
题意:给出两个长度相等的字符串,每次操作必须同时翻转两个字符串中相同长度的子串,求是否可以通过这种操作使得两个串相等
思路:可以推出当两个字符串的字符集相等,任一字符出现的次数不为一时,答案为YES。因为我们可以不断地翻转两个的相同字符,同时令另一个字符串不断地交换字符使得两个字符串相等。
这样我们可以把n优化到26,然后暴力翻转相邻的两个数即可,当翻转次数为偶数时,输出YES。
#includeB题
You are given a binary string of length n (i. e. a string consisting of n characters ‘0’ and ‘1’).
In one move you can swap two adjacent characters of the string. What is the lexicographically minimum possible string you can obtain from the given one if you can perform no more than k moves? It is possible that you do not perform any moves at all.
Note that you can swap the same pair of adjacent characters with indices i and i+1 arbitrary (possibly, zero) number of times. Each such swap is considered a separate move.
You have to answer q independent test cases.
The first line of the input contains one integer q (1≤q≤104) — the number of test cases.
The first line of the test case contains two integers n and k (1≤n≤106,1≤k≤n2) — the length of the string and the number of moves you can perform.
The second line of the test case contains one string consisting of n characters ‘0’ and ‘1’.
It is guaranteed that the sum of n over all test cases does not exceed 106 (∑n≤106).
For each test case, print the answer on it: the lexicographically minimum possible string of length n you can obtain from the given one if you can perform no more than k moves.
3
8 5
11011010
7 9
1111100
7 11
1111100
Output
01011110
0101111
0011111
题意:给你一串0 1 组成的数字,你可以修改他们的顺序,就是两两交换,一共可以进行K次操作,然后让他的字典序尽量的小(PS:0在前边的越多,字典序越小)-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
思路:想办法把0往前放就行!从i=0开始遍历,第一遇到0,看看能不能放到最前面,放完之后,记录一下放了几个了,然后一次进行就行了。
#includeC题

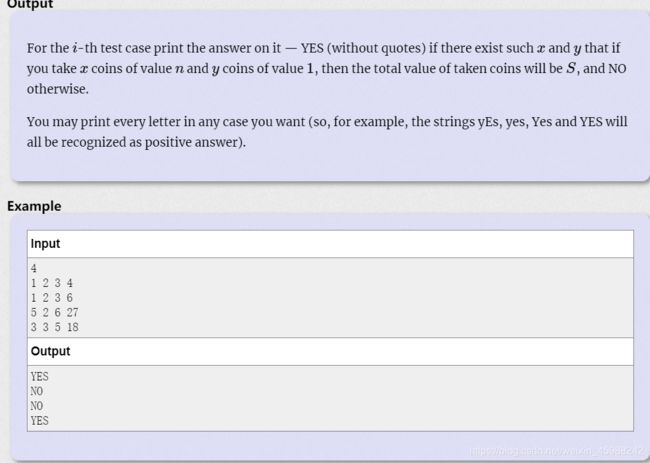
题意:a个n元和b个1元,问你能不能正好付s元!
思路:先判断钱够不够,(an+b)>=s再去判断能不能正好 就是用s/n,看得到的结果z;如果z>a,说明na不够,看看n*a+b>=s YES else NO
;如果z
else "YES"
#includeD题(还需 认真去理解啊 难)


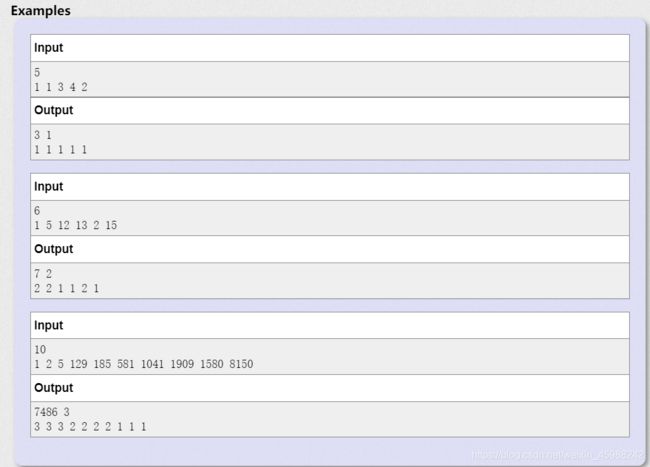

题意:给你序列让你分组,一组数最少3个,然后你需要去算每个组内的 【max-min】的和,然后让这个和尽量的小,输出和,组数
每个数的所属的组的号码!
思路:其实他最多也就5个人,因为>5之后他们就能分成两组了,这样差异肯定会变得更小所以最多也就五个人。
**
这个题目自己还没搞明白 感觉云里雾里的主要思路都没搞懂、。。。。。
Let’s sort all students by their programming skills but save the initial indices to restore the answer.
Now we can understand that we don’t need to compose the team of size greater than 5 because in this case we can split it into more teams with fewer participants and obtain the same or even less answer.
Now we can do the standard dynamic programming dpi— the minimum total diversity of the division if we divided the first i students (in sorted order). Initially, dp0=0, all other values of dp are +∞. Because of the fact above, we can do only three transitions (0-indexed):
dpi+3=min(dpi+3,dpi+ai+2−ai);
dpi+4=min(dpi+4,dpi+ai+3−ai);
dpi+5=min(dpi+5,dpi+ai+4−ai).
The answer is dpn and we can restore it by standard carrying parent values (as a parent of the state we can use, for example, the number of participants in the team). 这个官方题解
让我们根据学生的编程技能对他们进行分类,但是保存初始索引以恢复答案。
现在我们可以理解,我们不需要组成规模大于5的团队,因为在这种情况下,我们可以将其分成更多的团队,参与者更少,并获得相同或更少的答案。
现在我们可以做标准的动态编程dpi——如果我们把第一个I个学生分开(按排序的顺序),这个除法的最小总多样性。最初,dp0=0,dp的所有其他值为+∞。由于上述事实,我们只能进行三次转换(0索引):
dpi+3 =最小值(dpi+3,dpi+ai+2 ai);
dpi+4 =最小值(dpi+4,dpi+ai+3 ai);
dpi+5 =最小值(dpi+5,dpi+ai+4 ai)。
答案是dpn,我们可以通过携带父值的标准来恢复它(作为状态的父,我们可以使用,例如,团队中的参与者数量)。
#include
#define rpn(i,n) for(int i=1;i<=n;i++)
const int MAX_N=200005;
const int INF=int(1e9) +10;
p a[MAX_N];
int dp[MAX_N];//dp[i]前i个人最小的total diversity
int t[MAX_N];
int out[MAX_N];//用于输出
int main(){
int n;
scanf("%d",&n);
rpn(i,n){
scanf("%d",&a[i].fi);
a[i].sc=i;
}
sort(a+1,a+n+1);
fill(dp+1,dp+MAX_N,INF);
for(int i=0;i<n;i++){
for(int j=3;j<=5&&i+j<=n;j++){
int diff=a[i+j].fi-a[i+1].fi;
if(dp[i]+diff<dp[i+j]){
dp[i+j]=dp[i]+diff;
t[i+j]=j;//以第i+j人为结尾的队有t[i+j]人
}
}
}
int ans=0;
for(int i=n;i>=3;){
ans++;//第ans队,有t[i]人
int num=t[i];
while(num--) out[a[i--].sc]=ans;
}
printf("%d %d\n%d",dp[n],ans,out[1]);
for(int i=2;i<=n;i++) printf(" %d",out[i]);
return 0;
}
E题

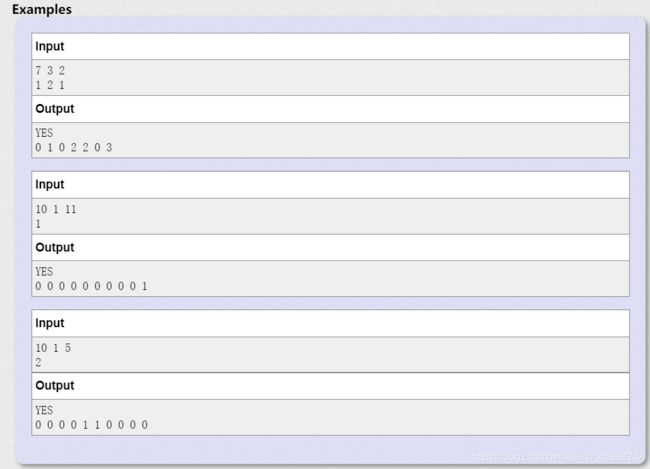

题意:输入 n,m,d;n就是河岸之间的距离,m是你几个不同长度的石头,d是你能跳的距离 就是你能在i最多跳到i+d的地方,问你能不能过桥,并输出河岸间 点的情况,如果铺了石头,输出 那个石头编号,没铺石头,就输出0;
思路:先判断能不能到达对岸,就是算你能走的距离是多少,首先石头就有距离,把石头距离s=a[i]的和,还有你每个石头都能跳,这个时候需要注意两点 你跳过的距离应该再算就是d-1了因为你石头距离已经算了,其次 你在起点的时候你就开始跳了,所以石头的数量是m+1。所以 距离是 (m + 1) * (d - 1)+s;
然后你设个标志代表自己到了那里了,然后你在进行跳,你需要设个变量考虑剩余的距离,以免到最后跳过头了!你跳的时候
tiao=min(sh,d-1);然后找个b数组来储存那个每个点上的数字就行了
#includeF题

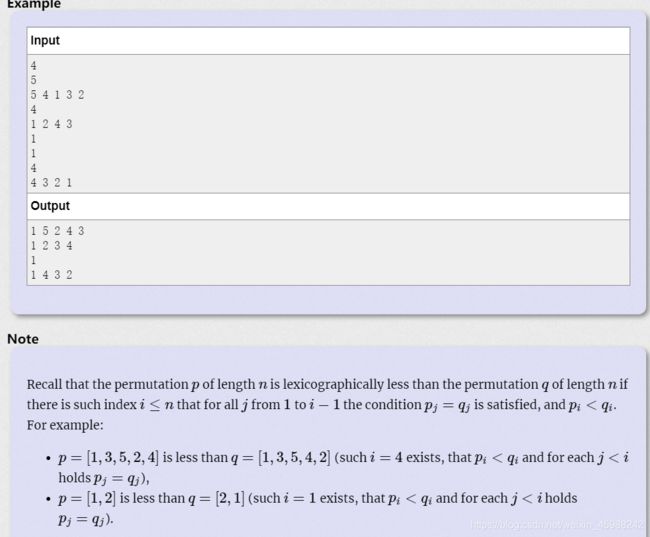
题意:给你序列 这些序列都是1-n之间的数,每个位置只能交换一次,问你最小的字典序的序列 。
思路:就是把小的数字往前排就行!一遍一遍的去遍历就可以,就是按着顺序找从1-n挨着找!!!找个数组记录这个位置有没有动过,然后开始往前移动,如果遇到瓶颈,就到此为止,然后再进行后续操作!最多进行n-1次操作;
#include感想:
感觉自己没把握好节奏吧,之前打cf都是从易到难,这个打乱顺序,
搞得自己也是半天才知道那些题简单,也浪费了时间吧,
还有读题不仔细,有很多细节方面没处理好。
有些题目确实自己平时做的不够好,比赛根本没怎么看过d之后的题目
现在出现在比赛中,自己也要认真搞定他们,难的话都难,但见多了,
就容易下手了!