中正平和的机器人学笔记——4. 雅可比矩阵(附MTALB代码)
1. 基础知识
基础知识主要是希望大家回顾一下大学物理里讲的速度矢量和角速度矢量部分的知识,用矢量形式去表示,还有叉乘的相关知识,这些我就不赘述了。
想象存在坐标系{A}和{B},把{B}固连在某一刚体上,要求描述 B Q ^BQ BQ相对于坐标系{A}的运动。
首先位置我们是可以确定的,用位置矢量 A P B O R G ^AP_{BORG} APBORG和旋转矩阵 B A R ^A_BR BAR来表示。那么求解速度也是一样的:
A V Q ^AV_Q AVQ = A V B O R G ^AV_{BORG} AVBORG + B A R ^A_BR BAR B V Q ^BV_Q BVQ
但是要注意,上式只适用于两坐标系姿态保持不变的情况!!
我们再考虑一种情况:两坐标系原点重合且相对线速度为零,固定在坐标系{B}上的矢量 B Q ^BQ BQ以角速度 A Ω B ^A\Omega_B AΩB相对于坐标系{A}旋转。那么从{A}看固定在{B}中的矢量是如何随时间变化呢?可以根据下图分析:
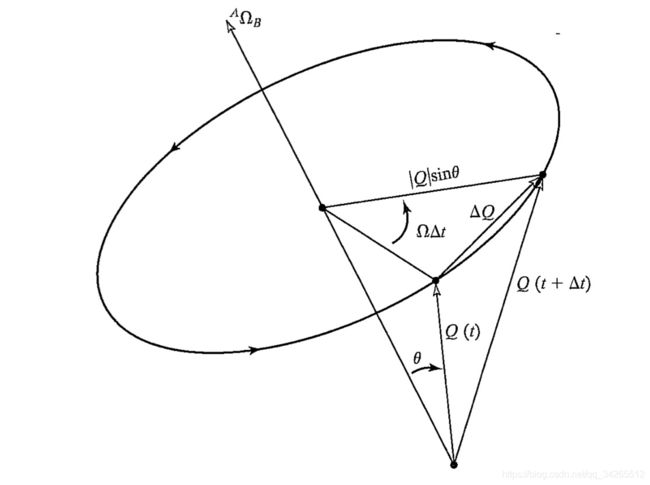
首先,显然 A Q ^AQ AQ的微分增量一定垂直于 A Ω B ^A\Omega_B AΩB和 A Q ^AQ AQ;
其次,可以看出微分增量的大小为| Δ Q \Delta Q ΔQ| = (| A Q ^AQ AQ sin θ \sin\theta sinθ|) (| A Ω B ^A\Omega_B AΩB| Δ t \Delta t Δt)
回顾大学物理的知识,我们可以得到
Q V Q ^QV_Q QVQ = A Ω B ^A\Omega_B AΩB × \times × A Q ^AQ AQ
而且一般情况下,Q是相对于{B}变化的,这就要加上一个分量,得到下式
A V Q ^AV_Q AVQ = A ( B V Q ) ^A(^BV_Q) A(BVQ) + A Ω B ^A\Omega_B AΩB × \times × A Q ^AQ AQ
A V Q ^AV_Q AVQ = B A R B V Q ^A_BR^BV_Q BARBVQ + A Ω B ^A\Omega_B AΩB × \times × B A R B Q ^A_BR^BQ BARBQ
实际上,我们也很容易将上式的情况扩展到原点不重合的情况,无非就是再加一个原点线速度的分量,那么最终我们就可以推导出从固定坐标系观测运动坐标系中的矢量导数的最终结果:
A V Q ^AV_Q AVQ = A V B O R G ^AV_{BORG} AVBORG + B A R B V Q ^A_BR^BV_Q BARBVQ + A Ω B ^A\Omega_B AΩB × \times × B A R B Q ^A_BR^BQ BARBQ
2. 连杆的速度“传递”
就如同位姿可以通过连杆间的推导从基座标推导到末端坐标系一样,线速度与角速度也可以。
首先我们看角速度。
当两个ω矢量都是相对于相同坐标系的时候,二者可以相加。那么i+1的角速度就等于连杆i的角速度加一个由于i+1角速度引起的分量,参照坐标系{i}就可以推导出:
i ω i + 1 ^i\omega_{i+1} iωi+1 = i ω i ^i\omega_i iωi + i + 1 i R _{i+1}^iR i+1iR θ ˙ i + 1 \dot{θ}_{i+1} θ˙i+1 i + 1 Z ^ i + 1 ^{i+1}\hat{Z}_{i+1} i+1Z^i+1
式中
θ ˙ i + 1 \dot{\theta}_{i+1} θ˙i+1 i + 1 Z ^ i + 1 ^{i+1}\hat{Z}_{i+1} i+1Z^i+1 = i + 1 ( 0 0 θ ˙ i + 1 ) ^{i+1}\begin{pmatrix}0\\0\\ \dot{\theta}_{i+1}\end{pmatrix} i+1⎝⎛00θ˙i+1⎠⎞
上式中我们给两边同时左乘 i i + 1 R ^{i+1}_iR ii+1R,最终要得到连杆i+1的角速度相对于坐标系{i+1}的表达式:
i + 1 ω i + 1 ^{i+1}\omega_{i+1} i+1ωi+1 = i i + 1 R _i^{i+1}R ii+1R i ω i ^i\omega_i iωi + θ ˙ i + 1 \dot{θ}_{i+1} θ˙i+1 i + 1 Z ^ i + 1 ^{i+1}\hat{Z}_{i+1} i+1Z^i+1
接下来看线速度。
坐标系{i+1}的原点的线速度等于坐标系{i}原点的线速度加上一个由于连杆i+1的角速度引起的分量,这与我么再第0节推导的结果一样,不是很清楚的可以回到上面再仔细看看,因此我们可以得到
i v i + 1 ^iv_{i+1} ivi+1 = i v i ^iv_i ivi + i ω i ^i\omega_i iωi × \times × i P i + 1 ^iP_{i+1} iPi+1
同样的两边左乘 i i + 1 R ^{i+1}_iR ii+1R,得到
i + 1 v i + 1 ^{i+1}v_{i+1} i+1vi+1 = i i + 1 R _i^{i+1}R ii+1R ( i v i + i ω i × i P i + 1 ) \left( \ ^iv_i+ ^i\omega_i \times ^iP_{i+1} \right) ( ivi+iωi×iPi+1)
这两个重要的公式希望大家能够好好理解:
i + 1 ω i + 1 ^{i+1}\omega_{i+1} i+1ωi+1 = i i + 1 R _i^{i+1}R ii+1R i ω i ^i\omega_i iωi + θ ˙ i + 1 \dot{θ}_{i+1} θ˙i+1 i + 1 Z ^ i + 1 ^{i+1}\hat{Z}_{i+1} i+1Z^i+1
i + 1 v i + 1 ^{i+1}v_{i+1} i+1vi+1 = i i + 1 R _i^{i+1}R ii+1R ( i v i + i ω i × i P i + 1 ) \left( \ ^iv_i+ ^i\omega_i \times ^iP_{i+1} \right) ( ivi+iωi×iPi+1)
以上是对于旋转关节的情况,如果是移动关节,那么公式就是下面的形式:
i + 1 ω i + 1 ^{i+1}\omega_{i+1} i+1ωi+1 = i i + 1 R _i^{i+1}R ii+1R i ω i ^i\omega_i iωi
i + 1 v i + 1 ^{i+1}v_{i+1} i+1vi+1 = i i + 1 R _i^{i+1}R ii+1R ( i v i + i ω i × i P i + 1 ) \left( \ ^iv_i+ ^i\omega_i \times ^iP_{i+1} \right) ( ivi+iωi×iPi+1) + d ˙ i + 1 \dot{d}_{i+1} d˙i+1 i + 1 Z ^ i + 1 ^{i+1}\hat{Z}_{i+1} i+1Z^i+1
我们可以通过一个平面两连杆机械臂来理解这组公式。
机械臂的参数以及坐标系确定如下,
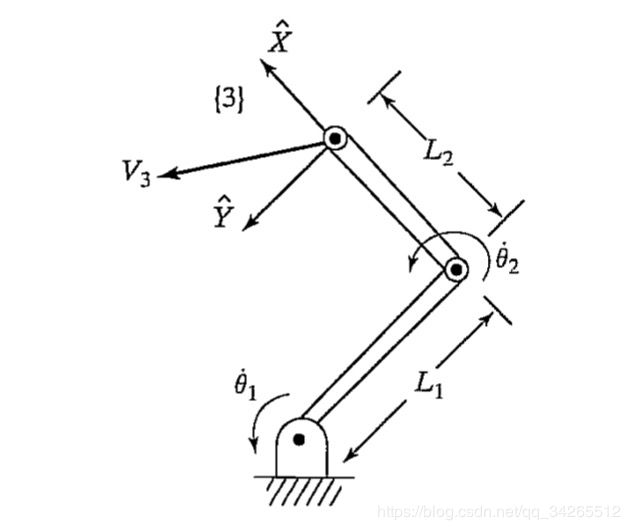
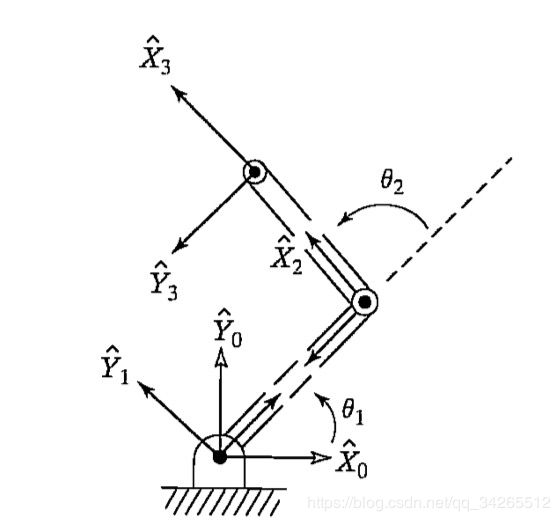
经过前面运动学的讲解,这里可以很容易地求出各个齐次变换矩阵
1 0 T ^0_1T 10T = ( c 1 − s 1 0 0 s 1 c 1 0 0 0 0 1 0 0 0 0 1 ) \begin{pmatrix} c_1 & -s_1 & 0 & 0 \\ s_1 & c_1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} ⎝⎜⎜⎛c1s100−s1c10000100001⎠⎟⎟⎞
2 1 T ^1_2T 21T = ( c 2 − s 2 0 l 1 s 2 c 2 0 0 0 0 1 0 0 0 0 1 ) \begin{pmatrix} c_2 & -s_2 & 0 & l_1 \\ s_2 & c_2 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} ⎝⎜⎜⎛c2s200−s2c2000010l1001⎠⎟⎟⎞
3 2 T ^2_3T 32T = ( 1 0 0 l 2 0 1 0 0 0 0 1 0 0 0 0 1 ) \begin{pmatrix} 1 & 0 & 0 & l_2 \\ 0 & 1& 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} ⎝⎜⎜⎛100001000010l2001⎠⎟⎟⎞
对各个连杆依次使用速度和角速度的两个公式:
i + 1 ω i + 1 ^{i+1}\omega_{i+1} i+1ωi+1 = i i + 1 R _i^{i+1}R ii+1R i ω i ^i\omega_i iωi + θ ˙ i + 1 \dot{θ}_{i+1} θ˙i+1 i + 1 Z ^ i + 1 ^{i+1}\hat{Z}_{i+1} i+1Z^i+1
i + 1 v i + 1 ^{i+1}v_{i+1} i+1vi+1 = i i + 1 R _i^{i+1}R ii+1R ( i v i + i ω i × i P i + 1 ) \left( \ ^iv_i+ ^i\omega_i \times ^iP_{i+1} \right) ( ivi+iωi×iPi+1)
我们可以得到,
1 ω 1 ^1\omega_1 1ω1 = ( 0 0 θ ˙ 1 ) \begin{pmatrix} 0\\ 0\\ \dot\theta_1 \end{pmatrix} ⎝⎛00θ˙1⎠⎞
1 v 1 ^1v_1 1v1 = ( 0 0 0 ) \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} ⎝⎛000⎠⎞
2 ω 2 ^2\omega_2 2ω2 = ( 0 0 θ ˙ 1 + θ ˙ 2 ) \begin{pmatrix} 0\\ 0\\ \dot\theta_1 + \dot\theta_2 \end{pmatrix} ⎝⎛00θ˙1+θ˙2⎠⎞
2 v 2 ^2v_2 2v2 = ( c 2 s 2 0 − s 2 c 2 0 0 0 0 ) \begin{pmatrix} c_2 & s_2 & 0\\ -s_2 & c_2 & 0\\ 0 & 0 & 0 \end{pmatrix} ⎝⎛c2−s20s2c20000⎠⎞ ( 0 l 1 θ ˙ 1 0 ) \begin{pmatrix} 0\\ l_1\dot\theta_1\\ 0 \end{pmatrix} ⎝⎛0l1θ˙10⎠⎞ = ( l 1 s 2 θ ˙ 1 l 1 c 2 θ ˙ 1 0 ) \begin{pmatrix} l_1s_2\dot{\theta}_1 \\ l_1c_2\dot{\theta}_1 \\ 0 \end{pmatrix} ⎝⎛l1s2θ˙1l1c2θ˙10⎠⎞
3 ω 3 ^3\omega_3 3ω3 = 2 ω 2 ^2\omega_2 2ω2
3 ω 3 ^3\omega_3 3ω3 = ( l 1 s 2 θ ˙ 1 l 1 c 2 θ ˙ 1 + l 2 ( θ ˙ 1 + θ ˙ 2 ) 0 ) \begin{pmatrix} l_1s_2\dot{\theta}_1\\ l_1c_2\dot{\theta}_1 + l_2(\dot\theta_1 + \dot\theta_2)\\ 0 \end{pmatrix} ⎝⎛l1s2θ˙1l1c2θ˙1+l2(θ˙1+θ˙2)0⎠⎞
为了得到相对于基座标的速度和角速度,我们再给出旋转矩阵 3 0 R ^0_3R 30R
3 0 R ^0_3R 30R = 1 0 R ^0_1R 10R 2 1 R ^1_2R 21R 3 2 R ^2_3R 32R = ( c 12 − s 12 0 s 12 c 12 0 0 0 1 ) \begin{pmatrix} c_{12} & -s_{12} & 0\\ s_{12} & c_{12} & 0\\ 0 & 0 & 1 \end{pmatrix} ⎝⎛c12s120−s12c120001⎠⎞
那么通过这个变换,我们就可以得到,
0 v 3 ^0v_3 0v3 = ( − l 1 s 1 θ ˙ 1 − l 2 s 12 ( θ ˙ 1 + θ ˙ 2 ) l 1 c 1 θ ˙ 1 + l 2 c 12 ( θ ˙ 1 + θ ˙ 1 ) 0 ) \begin{pmatrix} -l_1s_1\dot{\theta}_1 - l_2s_{12}(\dot{\theta}_1 + \dot{\theta}_2)\\ l_1c_1\dot{\theta}_1 + l_2c_{12}(\dot{\theta}_1 + \dot{\theta}_1)\\ 0\end{pmatrix} ⎝⎛−l1s1θ˙1−l2s12(θ˙1+θ˙2)l1c1θ˙1+l2c12(θ˙1+θ˙1)0⎠⎞
3. 雅可比
紧接着上面的推导出的速度 0 v 3 ^0v_3 0v3,我们来讲一下雅可比矩阵。
简单地说,雅可比矩阵就是多维形式的导数,在这里它就是速度的映射,是一个时变的线性映射: Y ˙ \dot{Y} Y˙ = 0 J ( X ) X ˙ ^0J(X) \dot{X} 0J(X)X˙ 。
在机器人学中,我们通常有以下形式:
0 v ^0\boldsymbol{v} 0v = 0 J ( Θ ) Θ ˙ ^0J(\Theta) \dot{\Theta} 0J(Θ)Θ˙
0 v ^0\boldsymbol{v} 0v = ( 0 v 0 ω ) \begin{pmatrix} ^0v\\^0\omega \end{pmatrix} (0v0ω)
0 v ^0v 0v是3 × \times × 1的线速度矢量, 0 ω ^0\omega 0ω是3 × \times × 1的角速度矢量。
那么根据 0 v 3 ^0v_3 0v3 = ( − l 1 s 1 θ ˙ 1 − l 2 s 12 ( θ ˙ 1 + θ ˙ 2 ) l 1 c 1 θ ˙ 1 + l 2 c 12 ( θ ˙ 1 + θ ˙ 1 ) 0 ) \begin{pmatrix} -l_1s_1\dot{\theta}_1 - l_2s_{12}(\dot{\theta}_1 + \dot{\theta}_2)\\ l_1c_1\dot{\theta}_1 + l_2c_{12}(\dot{\theta}_1 + \dot{\theta}_1)\\ 0\end{pmatrix} ⎝⎛−l1s1θ˙1−l2s12(θ˙1+θ˙2)l1c1θ˙1+l2c12(θ˙1+θ˙1)0⎠⎞,我们就可以得到雅可比矩阵
0 J ^0J 0J = ( − l 1 s 1 − l 2 s 12 − l 2 s 1 2 l 1 c 1 + l 2 c 12 l 2 c 1 2 ) \begin{pmatrix} -l_1s_1- l_2s_{12} & -l_2s_12\\ l_1c_1 + l_2c_{12} & l_2c_12\\ \end{pmatrix} (−l1s1−l2s12l1c1+l2c12−l2s12l2c12)
另外再提一下,雅可比矩阵参考坐标系的变换。
已知坐标系{B}中的雅可比矩阵,即
( B v B ω ) \begin{pmatrix}^Bv \\^B\omega\end{pmatrix} (BvBω) = B v ^B\boldsymbol{v} Bv = B J ( Θ ) Θ ˙ ^BJ(\Theta)\dot{\Theta} BJ(Θ)Θ˙
容易得到{B}中 6 × \times × 1的速度矢量在{A}中的变换,
( A v A ω ) \begin{pmatrix}^Av \\^A\omega\end{pmatrix} (AvAω) = ( B A R 0 0 B A R ) \begin{pmatrix}^A_BR & 0\\0 & ^A_BR\end{pmatrix} (BAR00BAR) ( B v B ω ) \begin{pmatrix}^Bv \\^B\omega\end{pmatrix} (BvBω)
因此可以得到
( A v A ω ) \begin{pmatrix}^Av \\^A\omega\end{pmatrix} (AvAω) = ( B A R 0 0 B A R ) \begin{pmatrix}^A_BR & 0\\0 & ^A_BR\end{pmatrix} (BAR00BAR) B J ( Θ ) Θ ˙ ^BJ(\Theta)\dot{\Theta} BJ(Θ)Θ˙
显然,可以完成雅可比矩阵的参考坐标系的转换
A J ^AJ AJ = ( B A R 0 0 B A R ) \begin{pmatrix}^A_BR & 0\\0 & ^A_BR\end{pmatrix} (BAR00BAR) B J ( Θ ) ^BJ(\Theta) BJ(Θ)
4. 奇异性
根据线性代数中的知识,如果某个 Θ \Theta Θ值使得雅可比矩阵 J J J不可逆,那么这些位置就是机构的奇异位型(singularities of the mechanism) 或者简称 奇异性(singularitries)。
可以确定的是,工作空间的边界存在奇异位型。记得我们前面讲过机械臂两个轴共轴导致失去一个自由度的情况吗?这就是在工作空间内的奇异位型。在这种情况下,选择什么样的速度都无法使机械臂运动
5. MATLAB中的雅可比
多余的就不赘述了,直接讲如何在MATLAB中求雅可比以及雅可比的一些应用。
mdl_puma560
J = p560.jacob0(qn) %qn是默认的位姿之一,其他的有qs、q0等。
%好了,求解雅可比就这么简单。。。一句话
%注意,jacob0()求解的是将关节速度映射到世界坐标系中的末端执行器空间速度
%如果要求末端执行器在自身空间内的速度的话,用下面这句
Jn = jaconb(qn);
上面我们提到了雅可比的奇异性,那么在MATLAB中怎么判断呢?
不要被太多名词迷惑了,本质上就是在问你,如何判断矩阵的奇异性。答案很简单——是否满秩。
rank(J) %就完啦,完啦,啦,a......
jsingu(J) %这句话可以自动分析奇异性,得到的结果是q6可由q4表示
6. 总结
雅可比这一篇大概是耗费时间最多,内容最多的一篇,但是我依然感觉自己写的仍然有点少。事实也确实是这样,雅可比在机器人学中是很重要的知识点,还有力域中的雅可比,这一篇我也不打算讲了,在后面的动力学部分再考虑整理一下吧。
今天下午去看了深圳草莓音乐节,站得腰酸背痛。回学校后想了想还是回实验室把这篇写完。周末终于解放了,回寝洗漱!