李宏毅机器学习2016 第八讲 深度学习网络优化小诀窍
视频链接:李宏毅机器学习(2016)_演讲•公开课_科技_bilibili_哔哩哔哩
课程资源:Hung-yi Lee
课程相关PPT已经打包命名好了:链接:https://pan.baidu.com/s/1c3Jyh6S 密码:77u5
我的第七讲笔记:李宏毅机器学习2016 第七讲 反向传播
Tips for Deep Learning
本章节主要讲解了深度学习中的一些优化策略,针对不同的情况适用于不同的优化方法。
主要内容是:新的激活函数(new activation function),自适应的学习率(adaptive learning rate),提早停止(early stop),正则化(regularization),丢弃(dropout)。
1.问题定义
在训练网络的过程中,我们通常的评价标准是网络能否在训练数据上得到好的结果以及网络能否在测试数据集上取得好的结果。正如我们之前所说,训练神经网络只需要三步,就好像将大象放进冰箱那么简单,第一步定义一个函数集,即网络结构的选择;第二步是定义评价函数的好坏,即损失函数的选择;第三部是挑选一个最好的函数,即如果更新权重进行学习。
这里我们需要注意的一个概念是overfitting,很多时候我们会将网络在测试集上表现不好而称为过拟合,实际上在此之前需要检查网络在训练数据集上的表现是否足够好。此外,过拟合通常不是我们训练神经网络遇到的第一个问题,因为在数据量很大很大时,我们也很难能够达到过拟合,一般会先遇到的问题是网络在训练数据集上表现不好,这时就需要通过调整网络结构等方法进行优化。
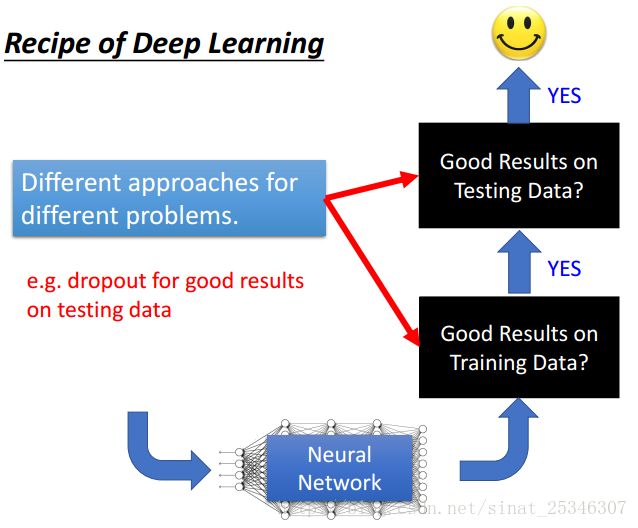
对于不同的情况我们会有不同的优化方法,每种症状对应的解决方法是不一样的。在深度学习中,我们要考虑每种方法的使用情况,对应于解决哪些问题。
本章节主要讲解了以下方法。
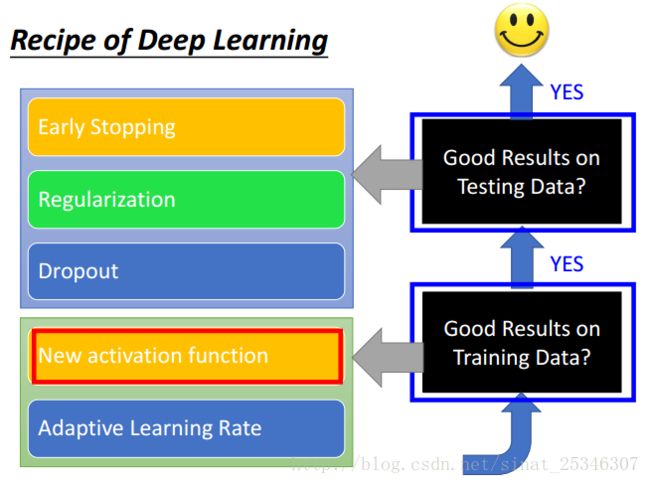
2. New Activation Function
通常如果出现网络性能在训练数据集上表现不好的时候,我们会调整网络结构,例如增加层数、神经元个数等。但这里需要注意的问题是越深不代表就会越好。
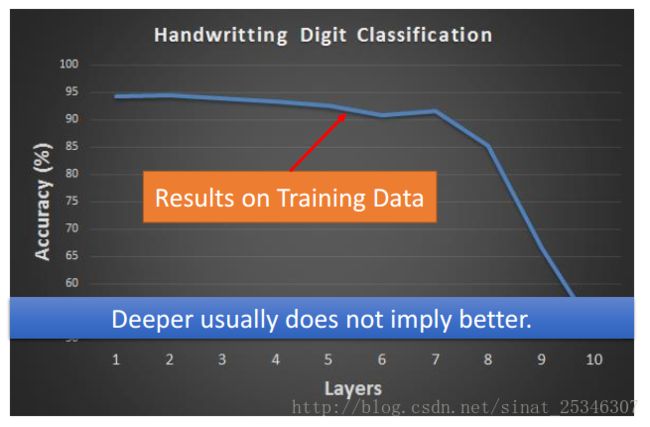
在此例中,准确率随着网络的层数反而会下降。这种情况并不能说因为函数太复杂了就是overfitting,因为过拟合一定要看其在训练数据上的表现,不能仅仅根据层数或者数量而言。
梯度消失问题(Vanishing Gradient Problem)

在靠近输出层的单元的梯度大,学习速度快,会一下子收敛,导致认为网络已经收敛了。
而靠近输入层的单元不会这样,梯度会小,学习起来慢,就相当于随机。
这样整个网络就好像是基于随机情况训练而来的。肯定会效果不好。
如果考虑将权重初始化大一点的值,这又有可能造成梯度爆炸问题。
出现此类问题的根本原因并非是消失的梯度问题或者爆炸的梯度问题,而是在前面的层上的梯度是来自后面的层上项的乘积。所以神经网络非常不稳定。
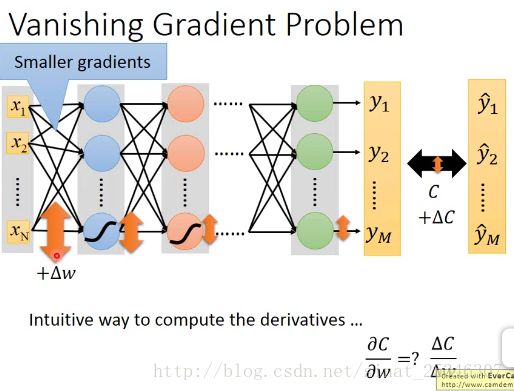
直觉的想法是在损失函数的对于权重的梯度变化对于靠近输入层上的梯度影响会极其小,这是因为sigmoid函数在很大的输入时,也是很小的输出。
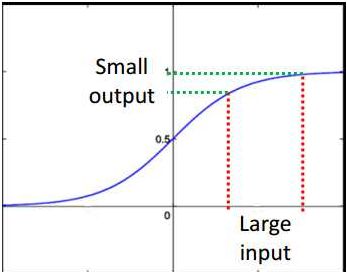
所以只要是sigmoid函数的神经网络都会造成梯度更新的时候极其不稳定,产生梯度消失或者爆炸问题。
解决方法可以用新的激活函数。

使用Relu激活函数最重要的一点是能够解决梯度消失的问题,在大于0的部分函数是线性的。
小于0时即为0,这就好像舍弃了部分单元,然后成为了一个瘦长的线性网络。可以理解为网络整体是线性的,而对input有着较大改变的,那就是非线性的。
此外还有别的进化版的Relu函数
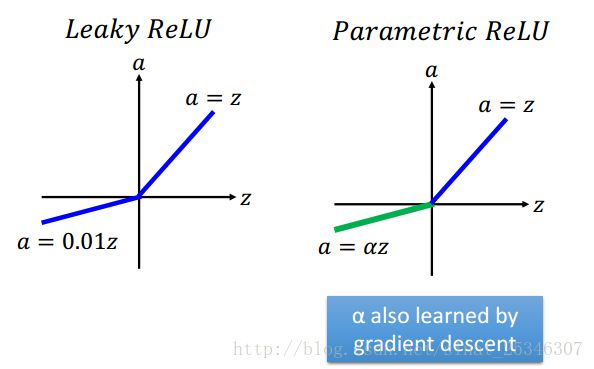
还有一种方法是Maxout,这是一种可学习的激活函数,其实Relu就是Maxout的一种特殊情况。
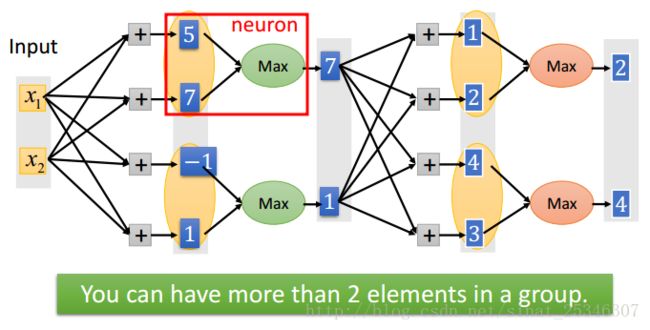
在Maxout中,将单元进行分组然后是一个max pooling的过程,这是分组是事先决定的。
分组是任意的,多少个元素单元在一个组就有多少片(pieces),这也就决定了激活函数是z怎样的分段线性凸函数。关于Maxout的训练和测试可类比与CNN中的Maxpooling。
2.Adaptive Learning Rate
在之前我们讲解了Adagrad方法更新学习率,使用了之前的偏导值去更新接下来的偏导值。

介绍下一种新的更好的方法RMSProp (Root Mean Square)

通过α的值大小可以设置不同的倾向方向。α小倾向于新的梯度值,大就倾向于之前的 值。
在训练网络中,我们经常担心会陷入局部最小值。但是其实不用过于担心这个问题,对于一个很大的神经网络,参数很多,其陷入局部最小值的概率是非常低的。
Momentum(动量方法)
此方法主要用了物理学上的惯性知识,当进行权值更新时,不仅要考虑此处的偏导值,也要考虑上一个状态的更新方向,两个方向的矢量和就是新的更新方向。

从上图的左部分就可以直觉看出,蓝色是动量方向,其值是由梯度值和上一步的动量值共同决定的。
我们也可以认为使用动量方向能够帮助我们跳出局部最小值。
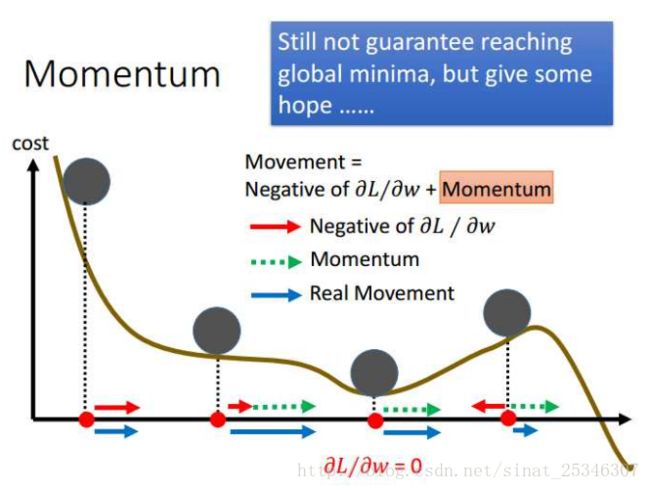
在梯度等于0的那个局部最小值点,上一步的动量方向会告诉我们应该继续往右而不是停止,进而能够在一定程度上跳出那个局部最小值点,虽然不能保证。
Adam
Adam的本质其实就是结合了上面讲的RMSProp和Momentum方法,此外还使用了一种偏差修置的方法。具体可看吴恩达深度学习课程 改善深层神经网络:超参数调试、正则化以及优化 - 网易云课堂 关于bias-corrected介绍。

3.Early Stopping
提早停止是一个较为传统的机器学习优化方法。
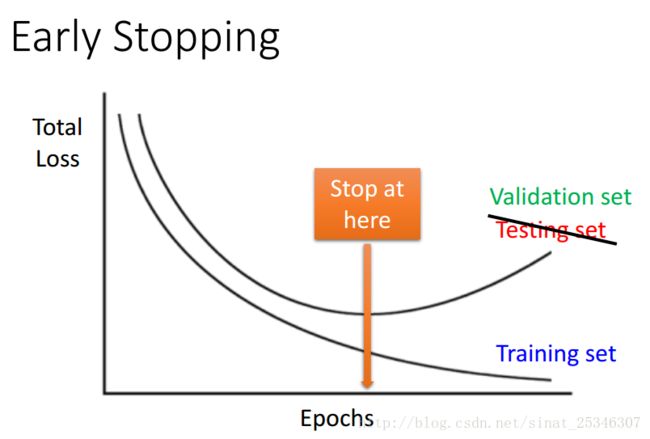
随着在训练数据上的损失不断减小,在验证集上的误差会在达到某个最小值后反而增大,这时可以考虑提早终止网络的训练,保留一个在训练集合验证集上效果都较好的网络。
4.Regularization
正则化在原来的损失函数上进行部分修改。
通过下式,我们可以看到L2正则化会带来权值衰减的效果。

其实正则化在深度学习中的作用并没有像在传统的机器学习(SVM)中作用那么大。
此外还有别的正则化方法,L1 regularization

L1的方法每次都是减去一个固定值,权值前系数大于0就加小于0则减。而L2是在前权值上有一个乘积的效果,训练起来会更快。
此外,需要注意L1方法会使得权值接近0,更加稀疏。
5.dropout
dropout是以一定的概率丢弃部分单元,这样网络就简化了。
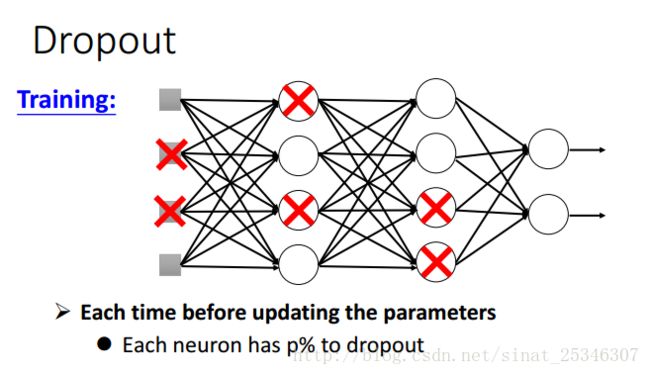
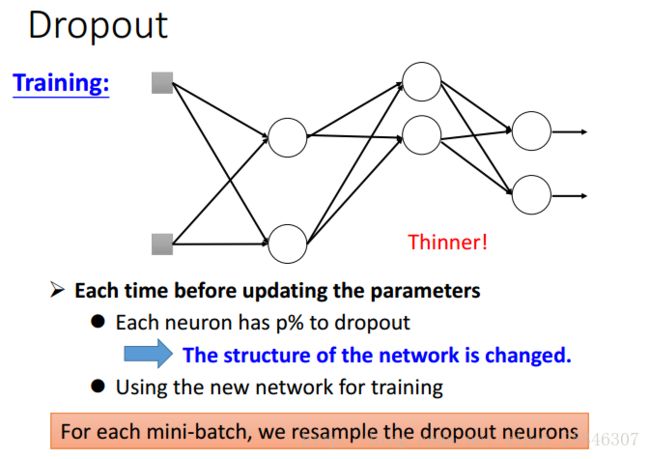
对于每一个min-batch,我们都要重新进行drouput,改变网络的结构,并使用新的网络结构去训练。
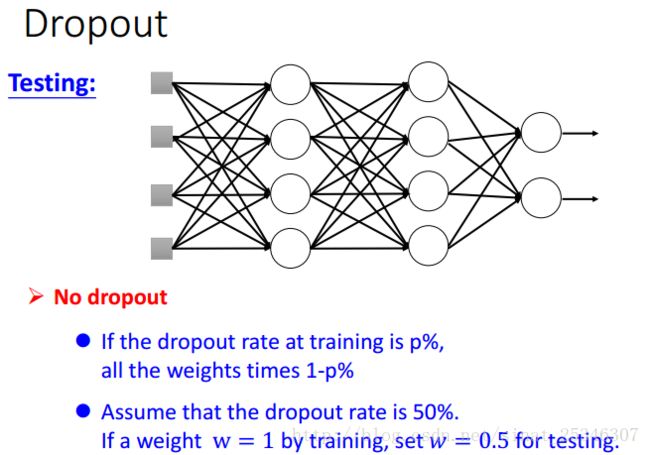
在测试时,是不能dropout的,并且要将权值都乘上1-p系数。
为什么要这么做,原因有很多。

较为直觉的想法是训练时脚上绑重物,在测试时拿下了重物后就会变得很强。
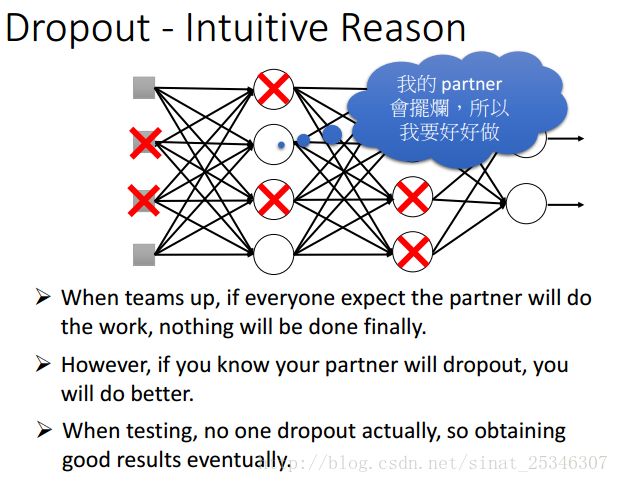
还可以理解为分组做project时,组队时都认为队友不会做(dropout),然后只能靠自己一个人好好做,到测试时,没有一个人不做,都好好做,效果就很好。
测试时为什么要乘1-p呢?
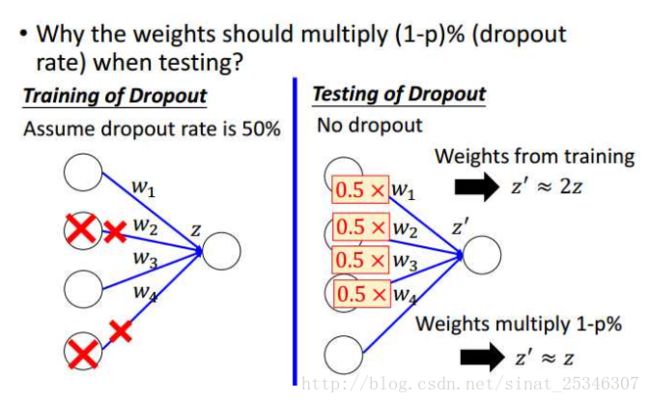
可以像上图这样理解,p为0.5时,在测试阶段得到的值会等于训练时的两倍,所以乘上1-p的系数就可使二者近似相等。
还可以理解dropout为一种集成。
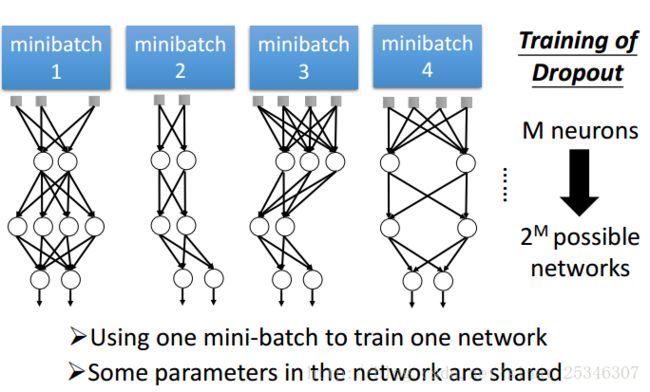 在训练时,有很多种的可能,测试时不可能全部记住这些网络结构,所以考虑乘上1-p的系数,认为二者近似相等。
在训练时,有很多种的可能,测试时不可能全部记住这些网络结构,所以考虑乘上1-p的系数,认为二者近似相等。
考虑一种较为简单的线性情况:
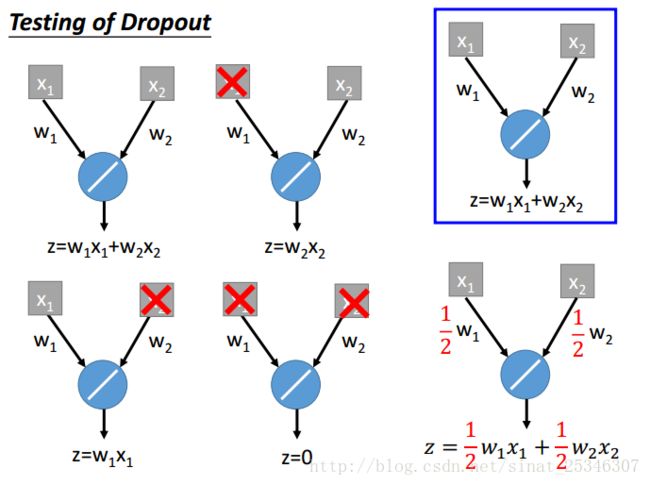
两个单元,四种情况,其可能取平均就等于最后全结构乘上1-p。
对于线性来说,这无疑会相等,非线性不会完全相等,但可认为是近似相等,有用。
6.总结
本章节内容较多而且比较重要。主要知识点在于介绍优化网络,处理不同网络问题的方法。
主要介绍了Relu激活函数、Adam更新权值、early stop、正则化以及dropout。