tensorflow笔记（1）-- 神经网络优化

有一些基础的神经网络的知识，在前面的一些博客有提及，网上也有很多相关基础的讲解，接下来是基础神经网络下，我觉得较为重要的神经网络的知识和关于改进神经网络的一些理解，当然也是搬运工，很多知识也在其他博客和公开课里面有提及，这里所涉及的大部分知识也是来源于公开课上的知识的一部分总结。神经网络的优化从以下五个方面叙述：

1.损失函数

2.学习率

3.滑动平均

4.正则化

5.神经网络搭建八股

一、损失函数

从一个简单的题目开始：

预测酸奶日销量y，x1 和 x2 是影响日销量的两个因素。

应提前采集的数据有：一段时间内，每日的 x1 因素、x2 因素和销量 y_。采集的数据尽量多。在本例中用销量预测产量，最优的产量应该等于销量。由于目前没有数据集，所以拟造了一套数据集。利用 Tensorflow 中函数随机生成 x1、 x2，制造标准答案 y_ = x1 + x2，为了更真实，求和后还加了正负 0.05 的随机噪声。我们把这套自制的数据集喂入神经网络，构建一个一层的神经网络，拟合预测酸奶日销量的函数。

代码如下：相对应的步骤和注释也可以看一下：

#coding:utf-8
#预测多或预测少的影响一样
#0导入模块，生成数据集
import tensorflow as tf
import numpy as np
BATCH_SIZE = 8              # 每次喂入的数据量大小
SEED = 23455                # 产生的随机种子的数量

rdm = np.random.RandomState(SEED)
X = rdm.rand(32,2)                       # rdm.rand的作用是产生一个0-1之间的随机数，这里代表产生0-1的随机数放在32行2列里面x1和x2
# 构建标准答案
Y_ = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X]
# 生成前闭后开区间随机数除以10变成0-0.1之间的随机数-0.05，则变成了-0.05-（+0.05）之间的随机数，取出x1和x2

# 1定义神经网络的输入、参数和输出，定义前向传播过程。
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
w1 = tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
y = tf.matmul(x, w1)

# 2定义损失函数及反向传播方法。
# 定义损失函数为MSE,反向传播方法为梯度下降。
loss_mse = tf.reduce_mean(tf.square(y_ - y))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss_mse)

# 3生成会话，训练STEPS轮
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 20000
    for i in range(STEPS):
        start = (i*BATCH_SIZE) % 32
        end = (i*BATCH_SIZE) % 32 + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})
        if i % 500 == 0:
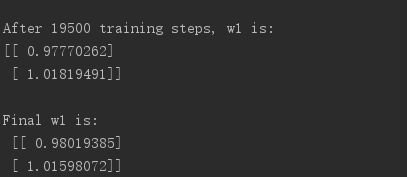
            print ("After %d training steps, w1 is: " % (i))
            print (sess.run(w1), "\n")
    print ("Final w1 is: \n", sess.run(w1))

打印出结果可以看到：

即得到相对应的关系是：

Y=X*0.98+1.02

由上述代码可知，本例中神经网络预测模型为 y = w1*x1 + w2*x2，损失函数采用均方误差。通过使损失函数值（loss）不断降低，神经网络模型得到最终参数 w1=0.98，w2=1.02，销量预测结果为 y = 0.98*x1 + 1.02*x2。由于在生成数据集时，标准答案为 y = x1 + x2，因此，销量预测结果和标准答案已非常接近，说明该神经网络预测酸奶日销量正确。

这里需要注意的几个tensorflow的几个重要的定义：

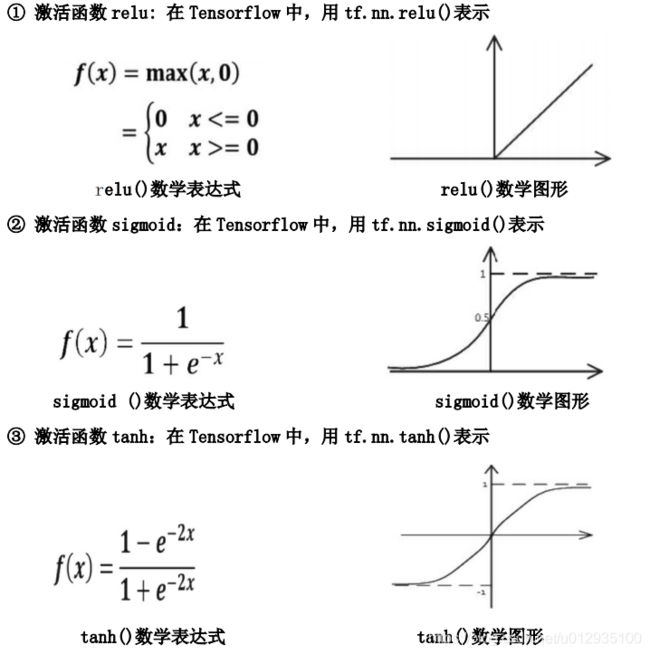
激活函数：引入非线性激活因素，提高模型的表达力。

常用的激活函数有 relu、sigmoid、tanh 等。

神经网络的复杂度：可用神经网络的层数和神经网络中待优化参数个数表示

神经网路待优化的参数：神经网络中所有参数 w 的个数 + 所有参数 b 的个数

损失函数（loss）：用来表示预测值（y）与已知答案（y_）的差距。在训练神经网络时，通过不断改变神经网络中所有参数，使损失函数不断减小，从而训练出更高准确率的神经网络模型。常用的损失函数有均方误差、自定义和交叉熵等。

自定义损失函数：根据问题的实际情况，定制合理的损失函数。

对于预测酸奶日销量问题，如果预测销量大于实际销量则会损失成本；如果预测销量小于实际销量则会损失利润。在实际生活中，往往制造一盒酸奶的成本和销售一盒酸奶的利润是不等价的。因此，需要使用符合该问题的自定义损失函数。

1.若酸奶成本为 1 元，酸奶销售利润为 9 元，则制造成本小于酸奶利润，因此希望预测的结果 y 多一些。采用上述的自定义损失函数，训练神经网络模型。

代码如下：

tf.reduce_sum(tf.where(tf.greater(y,y_),COST(y-y_),PROFIT(y_-y)))代表，如果y>y_则输出COST(y-y_)，如果相反则输出PROFIT(y_-y)，然后将所有的值求和。

# coding:utf-8
# 酸奶成本1元， 酸奶利润9元
# 预测少了损失大，故不要预测少，故生成的模型会多预测一些
# 0导入模块，生成数据集
import tensorflow as tf
import numpy as np
BATCH_SIZE = 8
SEED = 23455
COST = 1
PROFIT = 9

rdm = np.random.RandomState(SEED)
X = rdm.rand(32,2)
Y = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X]

# 1定义神经网络的输入、参数和输出，定义前向传播过程。
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
w1= tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
y = tf.matmul(x, w1)

# 2定义损失函数及反向传播方法。
# 定义损失函数使得预测少了的损失大，于是模型应该偏向多的方向预测。
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_)*COST, (y_ - y)*PROFIT))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)

# 3生成会话，训练STEPS轮。
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 3000
    for i in range(STEPS):
        start = (i*BATCH_SIZE) % 32
        end = (i*BATCH_SIZE) % 32 + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
        if i % 500 == 0:
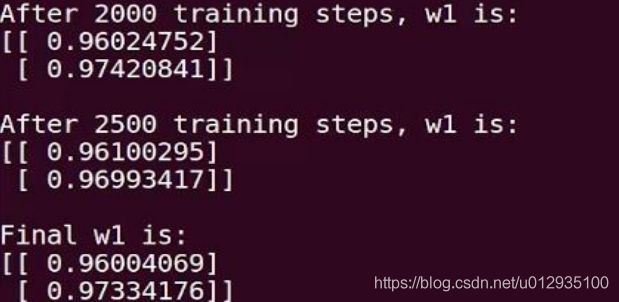
            print("After %d training steps, w1 is: " % (i))
            print(sess.run(w1), "\n")
    print("Final w1 is: \n", sess.run(w1))

相比于上面的代码只修改了损失函数，这里的输出是：

由代码执行结果可知，神经网络最终参数为 w1=1.03， w2=1.05，销量预测结果为 y =1.03*x1 +1.05*x2。由此可见，采用自定义损失函数预测的结果大于采用均方误差预测的结果，更符合实际需求。

2.若酸奶成本为 9 元，酸奶销售利润为 1 元，则制造成本大于酸奶利润，因此希望预测结果 y 小一些。采用上述的自定义损失函数，训练神经网络模型。

代码如下： 

#coding:utf-8
#酸奶成本9元， 酸奶利润1元
#预测多了损失大，故不要预测多，故生成的模型会少预测一些
#0导入模块，生成数据集
import tensorflow as tf
import numpy as np
BATCH_SIZE = 8
SEED = 23455
COST = 9
PROFIT = 1

rdm = np.random.RandomState(SEED)
X = rdm.rand(32,2)
Y = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X]

#1定义神经网络的输入、参数和输出，定义前向传播过程。
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
w1= tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
y = tf.matmul(x, w1)

#2定义损失函数及反向传播方法。
#重新定义损失函数，使得预测多了的损失大，于是模型应该偏向少的方向预测。
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_)*COST, (y_ - y)*PROFIT))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)

#3生成会话，训练STEPS轮。
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 3000
    for i in range(STEPS):
        start = (i*BATCH_SIZE) % 32
        end = (i*BATCH_SIZE) % 32 + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
        if i % 500 == 0:
            print "After %d training steps, w1 is: " % (i)
            print sess.run(w1), "\n"
    print "Final w1 is: \n", sess.run(w1)

这里只修改了部分参数，是酸奶的成本和利润修改了。那么输出是：

由执行结果可知，神经网络最终参数为 w1=0.96，w2=0.97，销量预测结果为 y =0.96*x1 + 0.97*x2。因此，采用自定义损失函数预测的结果小于采用均方误差预测的结果，更符合实际需求。

接下来是交叉熵的概念等。

交叉熵(Cross Entropy)：表示两个概率分布之间的距离。交叉熵越大，两个概率分布距离越远，两个概率分布越相异；交叉熵越小，两个概率分布距离越近，两个概率分布越相似。

交叉熵计算公式：?(?_ , ?) = −∑?_ ∗ ??? ?

用 Tensorflow 函数表示为

ce= -tf.reduce_mean(y_* tf.log(tf.clip_by_value(y, 1e-12, 1.0)))

例如：

两个神经网络模型解决二分类问题中，已知标准答案为 y_ = (1, 0)，第一个神经网络模型预测结果为y1=(0.6, 0.4)，第二个神经网络模型预测结果为 y2=(0.8, 0.2)，判断哪个神经网络模型预测的结果更接近标准答案。根据交叉熵的计算公式得：

H1((1,0),(0.6,0.4)) = -(1*log0.6 + 0*log0.4) ≈ -(-0.222 + 0) = 0.222

H2((1,0),(0.8,0.2)) = -(1*log0.8 + 0*log0.2) ≈ -(-0.097 + 0) = 0.097

由于 0.222>0.097，所以预测结果 y2 与标准答案 y_更接近，y2 预测更准确。

二、学习率

学习率（learning_rate）：表示了每次参数更新的幅度大小。学习率过大，会导致待优化的参数在最小值附近波动，不收敛；学习率过小，会导致待优化的参数收敛缓慢。在训练过程中，参数的更新向着损失函数梯度下降的方向。

参数的更新公式为：

由图可知，损失函数 loss 的最小值会在(-1,0)处得到，此时损失函数的导数为 0,得到最终参数 w =-1。代码如下：

#coding:utf-8
#设损失函数 loss=(w+1)^2, 令w初值是常数5。反向传播就是求最优w，即求最小loss对应的w值
import tensorflow as tf
#定义待优化参数w初值赋5
w = tf.Variable(tf.constant(5, dtype=tf.float32))
#定义损失函数loss
loss = tf.square(w+1)
#定义反向传播方法
train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)
#生成会话，训练40轮
with tf.Session() as sess:
    init_op=tf.global_variables_initializer()
    sess.run(init_op)
    for i in range(40):
        sess.run(train_step)
        w_val = sess.run(w)
        loss_val = sess.run(loss)
        print("After %s steps: w is %f,   loss is %f." % (i, w_val,loss_val))

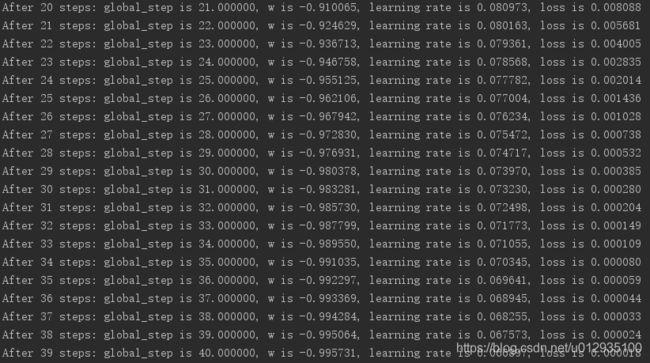
运行结果是：

街区了一部分运行结果，可以看出：

随着损失函数值的减小，w 无限趋近于-1，模型计算推测出最优参数 w = -1。

 学习率的设置：学习率过大，会导致待优化的参数在最小值附近波动，不收敛；学习率过小，会导致待优化的参数收

敛缓慢。

例如：

① 将上述代码中学习率修改为 1，其余内容不变。损失函数 loss 值并没有收敛，会在 5 和-7 之间波动。

② 将上述代码中学习率修改为 0.0001，其余内容不变。损失函数 loss 值缓慢下降，w 值也在小幅度变化，收敛缓慢。

指数衰减学习率：学习率随着训练轮数变化而动态更新。

例如，模型训练过程不设定固定的学习率，使用指数衰减学习率进行训练。其中，学习率初值设置为 0.1，学习率衰减率设置为 0.99，BATCH_SIZE 设置为 1。

代码如下：

#coding:utf-8
#设损失函数 loss=(w+1)^2, 令w初值是常数10。反向传播就是求最优w，即求最小loss对应的w值
#使用指数衰减的学习率，在迭代初期得到较高的下降速度，可以在较小的训练轮数下取得更有收敛度。
import tensorflow as tf

LEARNING_RATE_BASE = 0.1 #最初学习率
LEARNING_RATE_DECAY = 0.99 #学习率衰减率
LEARNING_RATE_STEP = 1  #喂入多少轮BATCH_SIZE后，更新一次学习率，一般设为：总样本数/BATCH_SIZE

#运行了几轮BATCH_SIZE的计数器，初值给0, 设为不被训练
global_step = tf.Variable(0, trainable=False)
#定义指数下降学习率
learning_rate = tf.train.exponential_decay(LEARNING_RATE_BASE, global_step, LEARNING_RATE_STEP, LEARNING_RATE_DECAY, staircase=True)
#定义待优化参数，初值给10
w = tf.Variable(tf.constant(5, dtype=tf.float32))
#定义损失函数loss
loss = tf.square(w+1)
#定义反向传播方法
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
#生成会话，训练40轮
with tf.Session() as sess:
    init_op=tf.global_variables_initializer()
    sess.run(init_op)
    for i in range(40):
        sess.run(train_step)
        learning_rate_val = sess.run(learning_rate)
        global_step_val = sess.run(global_step)
        w_val = sess.run(w)
        loss_val = sess.run(loss)
        print("After %s steps: global_step is %f, w is %f, learning rate is %f, loss is %f" % (i, global_step_val, w_val, learning_rate_val, loss_val))

运行结果如下：

由结果可以看出，随着训练轮数增加学习率在不断减小。

三、滑动平均

滑动平均：记录了一段时间内模型中所有参数 w 和 b 各自的平均值。利用滑动平均值可以增强模型的泛化能力。

代码如下：

# coding:utf-8
import tensorflow as tf

# 1. 定义变量及滑动平均类
# 定义一个32位浮点变量，初始值为0.0  这个代码就是不断更新w1参数，优化w1参数，滑动平均做了个w1的影子
w1 = tf.Variable(0, dtype=tf.float32)
# 定义num_updates（NN的迭代轮数）,初始值为0，不可被优化（训练），这个参数不训练
global_step = tf.Variable(0, trainable=False)
# 实例化滑动平均类，给衰减率为0.99，当前轮数global_step
MOVING_AVERAGE_DECAY = 0.99
ema = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY, global_step)
# ema.apply后的括号里是更新列表，每次运行sess.run（ema_op）时，对更新列表中的元素求滑动平均值。
# 在实际应用中会使用tf.trainable_variables()自动将所有待训练的参数汇总为列表
# ema_op = ema.apply([w1])
ema_op = ema.apply(tf.trainable_variables())

# 2. 查看不同迭代中变量取值的变化。
with tf.Session() as sess:
    # 初始化
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    # 用ema.average(w1)获取w1滑动平均值 （要运行多个节点，作为列表中的元素列出，写在sess.run中）
    # 打印出当前参数w1和w1滑动平均值
    print("current global_step:", sess.run(global_step))
    print("current w1", sess.run([w1, ema.average(w1)]))

    # 参数w1的值赋为1
    sess.run(tf.assign(w1, 1))
    sess.run(ema_op)
    print("current global_step:", sess.run(global_step))
    print("current w1", sess.run([w1, ema.average(w1)]))

    # 更新global_step和w1的值,模拟出轮数为100时，参数w1变为10, 以下代码global_step保持为100，每次执行滑动平均操作，影子值会更新
    sess.run(tf.assign(global_step, 100))
    sess.run(tf.assign(w1, 10))
    sess.run(ema_op)
    print("current global_step:", sess.run(global_step))
    print("current w1:", sess.run([w1, ema.average(w1)]))

    # 每次sess.run会更新一次w1的滑动平均值
    sess.run(ema_op)
    print("current global_step:", sess.run(global_step))
    print("current w1:", sess.run([w1, ema.average(w1)]))

    sess.run(ema_op)
    print("current global_step:", sess.run(global_step))
    print("current w1:", sess.run([w1, ema.average(w1)]))

    sess.run(ema_op)
    print("current global_step:", sess.run(global_step))
    print("current w1:", sess.run([w1, ema.average(w1)]))

    sess.run(ema_op)
    print("current global_step:", sess.run(global_step))
    print("current w1:", sess.run([w1, ema.average(w1)]))

    sess.run(ema_op)
    print("current global_step:", sess.run(global_step))
    print("current w1:", sess.run([w1, ema.average(w1)]))

    sess.run(ema_op)
    print("current global_step:", sess.run(global_step))
    print("current w1:", sess.run([w1, ema.average(w1)]))

# 更改MOVING_AVERAGE_DECAY 为 0.1  看影子追随速度

"""

current global_step: 0
current w1 [0.0, 0.0]
current global_step: 0
current w1 [1.0, 0.9]
current global_step: 100
current w1: [10.0, 1.6445453]
current global_step: 100
current w1: [10.0, 2.3281732]
current global_step: 100
current w1: [10.0, 2.955868]
current global_step: 100
current w1: [10.0, 3.532206]
current global_step: 100
current w1: [10.0, 4.061389]
current global_step: 100
current w1: [10.0, 4.547275]
current global_step: 100
current w1: [10.0, 4.9934072]

"""

 输出结果为：

从运行结果可知，最初参数 w1 和滑动平均值都是 0；参数 w1 设定为 1 后，滑动平均值变为 0.9；当迭代轮数更新为 100 轮时，参数 w1 更新为 10 后，滑动平均值变为 1.644。随后每执行一次，参数w1 的滑动平均值都向参数 w1 靠近。可见，滑动平均追随参数的变化而变化。

我们通常把训练过程和滑动平均放在一起运行，表示为：

with tf.control_dependencies([train_step, ema_op]): train_op = tf.no_op(name='train')

ema.average()函数返回滑动平均值

四、正则化

过拟合：神经网络模型在训练数据集上的准确率较高，在新的数据进行预测或分类时准确率较低，说明模型的泛化能力差。

正则化：在损失函数中给每个参数 w 加上权重，引入模型复杂度指标，从而抑制模型噪声，减小过拟合。

cem的值的计算在第一节中已经给出了。

matplotlib 模块：Python 中的可视化工具模块，实现函数可视化。

函数 plt.scatter（）：利用指定颜色实现点(x,y)的可视化。

plt.scatter (x 坐标, y 坐标, c=”颜色”)

plt.show()

收集规定区域内所有的网格坐标点：

xx, yy = np.mgrid[起:止:步长, 起:止:步长] #找到规定区域以步长为分辨率的行列网格坐标点

grid = np.c_[xx.ravel(), yy.ravel()] #收集规定区域内所有的网格坐标点

plt.contour()函数：告知 x、y 坐标和各点高度，用 levels 指定高度的点描上颜色

plt.contour (x 轴坐标值, y 轴坐标值, 该点的高度, levels=[等高线的高度])

plt.show()

本例子的代码如下：
 

# coding:utf-8
# 0导入模块 ，生成模拟数据集
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

BATCH_SIZE = 30      # 随机喂入30个坐标点
seed = 2             # 随机种子为2
# 基于seed产生随机数
rdm = np.random.RandomState(seed)
# 随机数返回300行2列的矩阵，表示300组坐标点（x0,x1）作为输入数据集
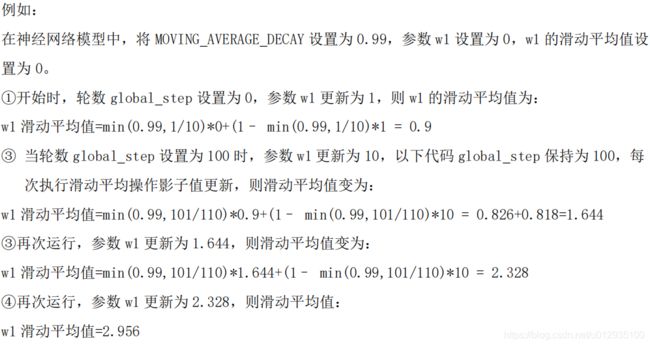
X = rdm.randn(300, 2)
# 从X这个300行2列的矩阵中取出一行,判断如果两个坐标的平方和小于2，给Y赋值1，其余赋值0
# 作为输入数据集的标签（正确答案）
Y_ = [int(x0 * x0 + x1 * x1 < 2) for (x0, x1) in X]
# 遍历Y中的每个元素，1赋值'red'其余赋值'blue'，这样可视化显示时人可以直观区分
Y_c = [['red' if y else 'blue'] for y in Y_]
# 对数据集X和标签Y进行shape整理，第一个元素为-1表示，随第二个参数计算得到，第二个元素表示多少列，把X整理为n行2列，把Y整理为n行1列
X = np.vstack(X).reshape(-1, 2)
Y_ = np.vstack(Y_).reshape(-1, 1)
print(X)
print(Y_)
print(Y_c)
# 用plt.scatter画出数据集X各行中第0列元素和第1列元素的点即各行的（x0，x1），用各行Y_c对应的值表示颜色（c是color的缩写）
plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(Y_c))     # X[:, 0]取X中的第一列元素，即x1,从Y_c取出对应位置赋给c
plt.show()


# 定义神经网络的输入、参数和输出，定义前向传播过程
def get_weight(shape, regularizer):        # 为了方便，我们定义了一个生成参数w的函数，函数的参数有：w的形状和正则化权重
    w = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w))
    return w


def get_bias(shape):             # 定义一个生成偏置b的函数，赋值为0.01
    b = tf.Variable(tf.constant(0.01, shape=shape))
    return b

# 给输入数据x和输入标签y_占位
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))

w1 = get_weight([2, 11], 0.01)     # w1为两行11列，注意shape都是以列的形式给出的，正则化权重为0.01
b1 = get_bias([11])              # b1为11个
y1 = tf.nn.relu(tf.matmul(x, w1) + b1)

w2 = get_weight([11, 1], 0.01)
b2 = get_bias([1])
y = tf.matmul(y1, w2) + b2

# 定义损失函数
loss_mse = tf.reduce_mean(tf.square(y - y_))
loss_total = loss_mse + tf.add_n(tf.get_collection('losses'))

# 定义反向传播方法：不含正则化
train_step = tf.train.AdamOptimizer(0.0001).minimize(loss_mse)

with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 40000
    for i in range(STEPS):
        start = (i * BATCH_SIZE) % 300
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})
        if i % 2000 == 0:
            loss_mse_v = sess.run(loss_mse, feed_dict={x: X, y_: Y_})
            print("After %d steps, loss is: %f" % (i, loss_mse_v))
            # xx在-3到3之间以步长为0.01，yy在-3到3之间以步长0.01,生成二维网格坐标点
    xx, yy = np.mgrid[-3:3:.01, -3:3:.01]
    # 将xx , yy拉直，并合并成一个2列的矩阵，得到一个网格坐标点的集合
    grid = np.c_[xx.ravel(), yy.ravel()]
    # 将网格坐标点喂入神经网络 ，probs为输出
    probs = sess.run(y, feed_dict={x: grid})
    # probs的shape调整成xx的样子
    probs = probs.reshape(xx.shape)
    print("w1:\n", sess.run(w1))
    print("b1:\n", sess.run(b1))
    print("w2:\n", sess.run(w2))
    print("b2:\n", sess.run(b2))

plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(Y_c))
plt.contour(xx, yy, probs, levels=[.5])
plt.show()

# 定义反向传播方法：包含正则化
train_step = tf.train.AdamOptimizer(0.0001).minimize(loss_total)

with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 40000
    for i in range(STEPS):
        start = (i * BATCH_SIZE) % 300
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})
        if i % 2000 == 0:
            loss_v = sess.run(loss_total, feed_dict={x: X, y_: Y_})
            print("After %d steps, loss is: %f" % (i, loss_v))

    xx, yy = np.mgrid[-3:3:.01, -3:3:.01]
    grid = np.c_[xx.ravel(), yy.ravel()]
    probs = sess.run(y, feed_dict={x: grid})
    probs = probs.reshape(xx.shape)
    print("w1:\n", sess.run(w1))
    print("b1:\n", sess.run(b1))
    print("w2:\n", sess.run(w2))
    print("b2:\n", sess.run(b2))

plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(Y_c))
plt.contour(xx, yy, probs, levels=[.5])
plt.show()

 运行结果是：

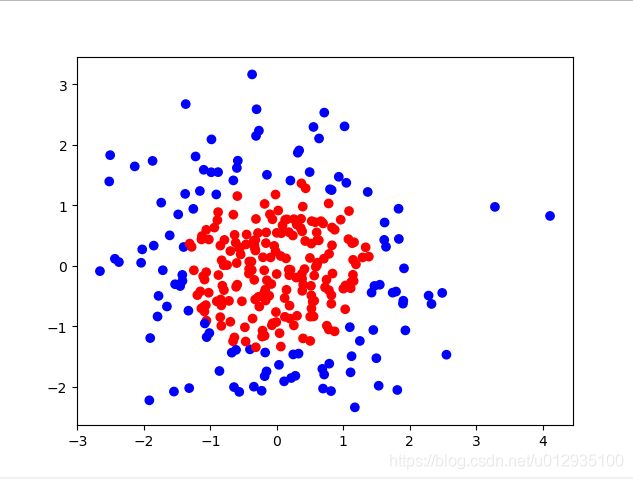
接着，执行无正则化的训练过程，把红色的点和蓝色的点分开，生成曲线如下图所示：

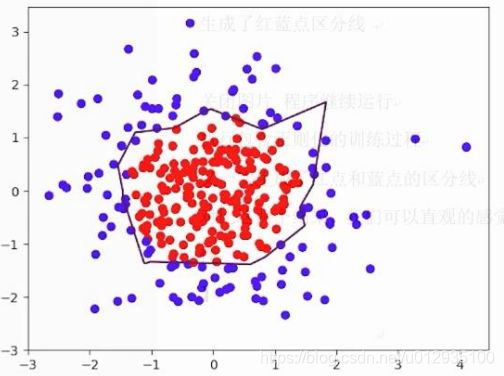
最后，执行有正则化的训练过程，把红色的点和蓝色的点分开，生成曲线如下图所示：

对比无正则化与有正则化模型的训练结果，可看出有正则化模型的拟合曲线平滑，模型具有更好的泛化能力。

注：正则化一般只对w使用，在损失函数中引入模型复杂度指标。

使用正则化后，loss变成两部分，如上面所述。

经过L1正则化或者L2正则化后，tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w) ，将所有计算好的正则化加在losses中，用tf.add_n(tf.get_collection('losses'))将所有loss相加

然后loss = cem + tf.add_n(tf.get_collection('losses'))，加上交叉熵，构成了总损失函数。

五、搭建模块化神经网络八股

程序因为复杂性，为了体现程序的层次性和可复用性，我们可以将程序进行模块化编写。

这里就涉及了前向传播和反向传播的八股：

1.前向传播：由输入到输出，搭建完整的网络结构

前向传播的程序一般用forward.py表示，定义三个函数：

def forward(x, regularizer):

w=

b=

y=

return y

第一个函数 forward()完成网络结构的设计，从输入到输出搭建完整的网络结构，实现前向传播过程。该函数中，参数 x 为输入，regularizer 为正则化权重，返回值为预测或分类结果 y。

def get_weight(shape, regularizer):

w = tf.Variable( )

tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w))

return w

第二个函数 get_weight()对参数 w 设定。该函数中，参数 shape 表示参数 w 的形状，regularizer表示正则化权重，返回值为参数 w。其中，tf.variable()给 w 赋初值，tf.add_to_collection()表示将参数 w 正则化损失加到总损失 losses 中。

def get_bias(shape):

b = tf.Variable( )

return b

第三个函数 get_bias()对参数 b 进行设定。该函数中，参数 shape 表示参数 b 的形状,返回值为参数b。其中，tf.variable()表示给 b 赋初值。

2.反向传播：训练网络，优化网络参数，提高模型准确性。

前向传播的程序一般用backward.py表示，定义backward函数：

def backward( ):

x = tf.placeholder( )

y_ = tf.placeholder( )

y = forward.forward(x, REGULARIZER)

global_step = tf.Variable(0, trainable=False)

loss =

其中loss可以为：

函数 backward()中，placeholder()实现对数据集 x 和标准答案 y_占位，forward.forward()实现前向传播的网络结构，参数 global_step 表示训练轮数，设置为不可训练型参数。

在训练网络模型时，常将正则化、指数衰减学习率和滑动平均这三个方法作为模型优化方法。

正则化loss值上面有提到，指数衰减学习率和滑动平均的方法如下：

在 Tensorflow 中，指数衰减学习率表示为：

在 Tensorflow 中，滑动平均表示为：

其中，滑动平均和指数衰减学习率中的 global_step 为同一个参数。

3.接下来要做的就是：用 with 结构初始化所有参数

with tf.Session() as sess:

        init_op = tf.global_variables_initializer()

              sess.run(init_op)

         for i in range(STEPS):

              sess.run(train_step, feed_dict={x: , y_: })

                     if i % 轮数 == 0:

                    print

其中，with 结构用于初始化所有参数信息以及实现调用训练过程，并打印出 loss 值。

4.判断 python 运行文件是否为主文件

if __name__=='__main__':

        backward()

该部分用来判断 python 运行的文件是否为主文件。若是主文件，则执行 backword()函数。

接下来就是结合例子来进行讲解：

代码总共分为三个模块：生成数据集 (generateds.py)、前向传播(forward.py)、反向传播(backward.py)。

①生成数据集的模块(generateds.py)

#coding:utf-8
#0导入模块 ，生成模拟数据集
import numpy as np
import matplotlib.pyplot as plt
seed = 2 
def generateds():
	#基于seed产生随机数
	rdm = np.random.RandomState(seed)
	#随机数返回300行2列的矩阵，表示300组坐标点（x0,x1）作为输入数据集
	X = rdm.randn(300,2)
	#从X这个300行2列的矩阵中取出一行,判断如果两个坐标的平方和小于2，给Y赋值1，其余赋值0
	#作为输入数据集的标签（正确答案）
	Y_ = [int(x0*x0 + x1*x1 <2) for (x0,x1) in X]
	#遍历Y中的每个元素，1赋值'red'其余赋值'blue'，这样可视化显示时人可以直观区分
	Y_c = [['red' if y else 'blue'] for y in Y_]
	#对数据集X和标签Y进行形状整理，第一个元素为-1表示跟随第二列计算，第二个元素表示多少列，可见X为两列，Y为1列
	X = np.vstack(X).reshape(-1,2)
	Y_ = np.vstack(Y_).reshape(-1,1)
	
	return X, Y_, Y_c
	
#print X
#print Y_
#print Y_c
#用plt.scatter画出数据集X各行中第0列元素和第1列元素的点即各行的（x0，x1），用各行Y_c对应的值表示颜色（c是color的缩写） 
#plt.scatter(X[:,0], X[:,1], c=np.squeeze(Y_c)) 
#plt.show()

②前向传播模块(forward.py)

#coding:utf-8
#0导入模块 ，生成模拟数据集
import tensorflow as tf

#定义神经网络的输入、参数和输出，定义前向传播过程 
def get_weight(shape, regularizer):
	w = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
	tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w))
	return w

def get_bias(shape):  
    b = tf.Variable(tf.constant(0.01, shape=shape)) 
    return b
	
def forward(x, regularizer):
	
	w1 = get_weight([2,11], regularizer)	
	b1 = get_bias([11])
	y1 = tf.nn.relu(tf.matmul(x, w1) + b1)

	w2 = get_weight([11,1], regularizer)
	b2 = get_bias([1])
	y = tf.matmul(y1, w2) + b2 
	
	return y

③反向传播模块(backward.py)

#coding:utf-8
#0导入模块 ，生成模拟数据集
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import opt4_8_generateds
import opt4_8_forward

STEPS = 40000
BATCH_SIZE = 30 
LEARNING_RATE_BASE = 0.001
LEARNING_RATE_DECAY = 0.999
REGULARIZER = 0.01

def backward():
	x = tf.placeholder(tf.float32, shape=(None, 2))
	y_ = tf.placeholder(tf.float32, shape=(None, 1))

	X, Y_, Y_c = opt4_8_generateds.generateds()       # 调用函数进行赋值

	y = opt4_8_forward.forward(x, REGULARIZER)
	
	global_step = tf.Variable(0,trainable=False)	

	learning_rate = tf.train.exponential_decay(
		LEARNING_RATE_BASE,
		global_step,
		300/BATCH_SIZE,
		LEARNING_RATE_DECAY,
		staircase=True)


	#定义损失函数
	loss_mse = tf.reduce_mean(tf.square(y-y_))              
	loss_total = loss_mse + tf.add_n(tf.get_collection('losses'))
	
	#定义反向传播方法：包含正则化
	train_step = tf.train.AdamOptimizer(learning_rate).minimize(loss_total)

	with tf.Session() as sess:
		init_op = tf.global_variables_initializer()
		sess.run(init_op)
		for i in range(STEPS):
			start = (i*BATCH_SIZE) % 300
			end = start + BATCH_SIZE
			sess.run(train_step, feed_dict={x: X[start:end], y_:Y_[start:end]})
			if i % 2000 == 0:
				loss_v = sess.run(loss_total, feed_dict={x:X,y_:Y_})
				print("After %d steps, loss is: %f" %(i, loss_v))

		xx, yy = np.mgrid[-3:3:.01, -3:3:.01]
        # 在-3到3之间以0.01的间距生成网格坐标点，组成xx,yy坐标集命名为grid,把它喂入神经网络，输出为probs，把probs整理形状后画出离散点，和probs为0.5的曲线
		grid = np.c_[xx.ravel(), yy.ravel()]
		probs = sess.run(y, feed_dict={x:grid})
		probs = probs.reshape(xx.shape)
	
	plt.scatter(X[:,0], X[:,1], c=np.squeeze(Y_c)) 
	plt.contour(xx, yy, probs, levels=[.5])
	plt.show()
	
if __name__=='__main__':
	backward()

代码中注释部分比较详细，部分没有注释，代码讲解之前博客和博客前面的章节里面也都有每一句代码对应的注释，所以这里就不多做做过的事情了，不懂的可以看一下前面的博客。

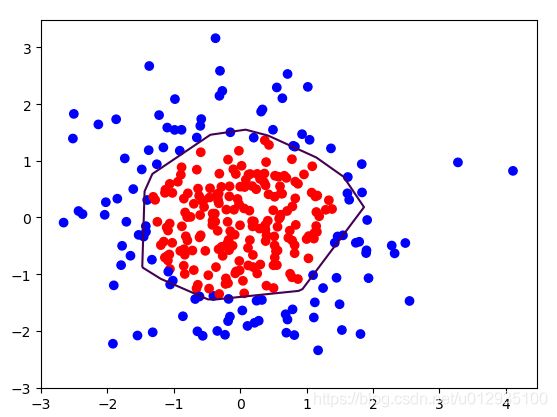
下面是代码的运行结果：

由运行结果可见，程序使用模块化设计方法，加入指数衰减学习率，使用正则化后，红色点和蓝色点的分割曲线相对平滑，效果变好。