6轴机器人运动学正解,逆解1
正解
给定机器人各关节的角度,计算出机器人末端的空间位置
逆解
已知机器人末端的位置和姿态,计算机器人各关节的角度值
常见的工业机器人

正解与逆解的求解需要相应的机器人运动方程,其中关键的就是DH参数表
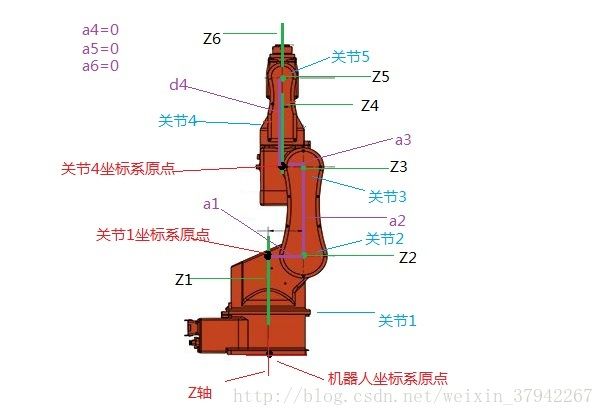
DH参数表用来描述机器人各关节坐标系之间的关系,有了DH参数表就可以在机器人各关节之间进行坐标转换
求解正解就是从关节1到关节5的坐标转换
基本知识
关节:连接2个杆件的部分
连杆长度 (a) :2个相邻关节轴线之间的距离
连杆扭角 (alpha α) :2个相邻关节轴线之间的角度
连杆偏距 (d) :2个关节坐标系的X轴之间的距离
关节角度 (theta θ) :关节变量 计算时需要加初始角度偏移
Z轴: 关节轴线
X轴: 从Z(i)轴指向Z(i+1)轴 与a重合
alpha: Z(i)轴绕X(i)轴旋转到Z(i+1)轴的角度
a: 相邻的2个关节轴线之间的距离是a Z(i)轴到Z(i+1)轴
d: 2个相邻的a之间的距离是d a(i-1)到a(i) 相邻X轴之间的距离
关节角度 从Z轴正向看原点 逆时针旋转为正
如果(a=0),X(i)与X(i-1)方向相同
如果(a!=0),X(i)从Z(i)指向Z(i+1)
DH参数表
| 关节 | a | d | α |
|---|---|---|---|
| 1 | 100 | 0 | 90 |
| 2 | 270 | 0 | 0 |
| 3 | 60 | 0 | 90 |
| 4 | 0 | 270 | -90 |
| 5 | 0 | 0 | 90 |
| 6 | 0 | 0 | 0 |
DH参数有多种表示方式,与坐标系及坐标轴的设定有关
正解的计算方法
机器人从关节1到关节6进行坐标变换,结果就是末端的位置坐标
根据DH参数表以及关节变量的值,建立6个关节矩阵A1-A6,计算出转换矩阵T1-T6,T1-T6相乘得出结果
6轴机器人4,5,6轴相交于1点 正解计算只算到第5轴
为简化矩阵计算,关节1坐标系原点设在Z2轴的水平平面上,最终结果在Z方向需要再加上一个偏移值
/* 4阶矩阵计算机器人正解
* 关节角度在文件 J1_J6中
* 机器人参数在文件 param_table中
* 坐标结果在屏幕输出 */
#include for(j=0; jprintf(" %lf ", matrix[i][j]);
}
printf("\n");
}
printf("\n");
}
void printmatrix_1(double matrix[MATRIX_N][1], int m, int n)
{
int i, j;
for(i=0; ifor(j=0; jprintf(" %lf ", matrix[i][j]);
}
printf("\n");
}
printf("\n");
}
int main()
{
double matrix_T1[MATRIX_N][MATRIX_N];
double matrix_T2[MATRIX_N][MATRIX_N];
double matrix_T3[MATRIX_N][MATRIX_N];
double matrix_T4[MATRIX_N][MATRIX_N];
double matrix_T5[MATRIX_N][MATRIX_N];
double matrix_T6[MATRIX_N][MATRIX_N];
//double j1=0, j2=0, j3=0, j4=0, j5=0, j6=0;
//double l1=0, l2=0, l3=0, d4=0, z_offset=0;
double toolx=0, tooly=0, toolz=0, toolrx=0, toolry=0, toolrz=0;
double worldx=0, worldy=0, worldz=0, worldrx=0, worldry=0, worldrz=0;
double z_offset=0;
param_t param_table[6] ={0};
memset(param_table, 0, sizeof(param_table) );
FILE * fp=NULL;
fp=fopen(XYZ_F_J, "r");
if(fp== NULL){
perror("open J1_J6 file error\n");
return 0;
}
fscanf(fp, "%lf%lf%lf%lf%lf%lf",
¶m_table[0].joint_v,
¶m_table[1].joint_v,
¶m_table[2].joint_v,
¶m_table[3].joint_v,
¶m_table[4].joint_v,
¶m_table[5].joint_v
);
printf("j1...j6\n%lf %lf %lf %lf %lf %lf\n",
param_table[0].joint_v,
param_table[1].joint_v,
param_table[2].joint_v,
param_table[3].joint_v,
param_table[4].joint_v,
param_table[5].joint_v
);
//加初始角度偏移 j2 j3
param_table[1].joint_v += ANGLE_OFFSET_J2;
param_table[2].joint_v += ANGLE_OFFSET_J3;
//将机器人关节角度转换成弧度
param_table[0].joint_v *= RAD2ANG;
param_table[1].joint_v *= RAD2ANG;
param_table[2].joint_v *= RAD2ANG;
param_table[3].joint_v *= RAD2ANG;
param_table[4].joint_v *= RAD2ANG;
param_table[5].joint_v *= RAD2ANG;
printf("\nj1...j6 RAD2ANG\n%lf %lf %lf %lf %lf %lf\n",
param_table[0].joint_v,
param_table[1].joint_v,
param_table[2].joint_v,
param_table[3].joint_v,
param_table[4].joint_v,
param_table[5].joint_v
);
fclose(fp);
fp=fopen(DESIGN_DT, "r");
if( fp== NULL){
perror("open param_table file error\n");
return 0;
}
//读入关节参数
int i;
for(i=0; i<6; i++){
fscanf(fp, "%lf%lf%lf",
¶m_table[i].length,
¶m_table[i].d,
¶m_table[i].angle );
}
fscanf(fp, "%lf", &z_offset );
fclose(fp);
param_table[0].angle *= RAD2ANG;
param_table[1].angle *= RAD2ANG;
param_table[2].angle *= RAD2ANG;
param_table[3].angle *= RAD2ANG;
param_table[4].angle *= RAD2ANG;
param_table[5].angle *= RAD2ANG;
initmatrix_A(param_table);
/*
//fscanf(fp, "%lf %lf %lf", &toolx, &tooly, &toolz);
//printf("tool x y z\n%lf %lf %lf\n", toolx, tooly, toolz);
fp=fopen(XYZ_F_TOOL, "r");
if(fp== NULL || DEF_TOOLXYZ == 0){
printf("no toolxyz \n");
}else{
fscanf(fp, "%lf %lf %lf %lf %lf %lf",
&toolx, &tooly, &toolz, &toolrx, &toolry, &toolrz);
printf("\ntoolxyz\n%lf %lf %lf %lf %lf %lf\n",
toolx, tooly, toolz, toolrx, toolry, toolrz);
fclose(fp);
}
initmatrix_tool(toolx, tooly, toolz);
*/
//计算变换矩阵 matrix T1---T6
matrix_copy(matrix_A1, matrix_T1, MATRIX_N, MATRIX_N);
printf("matrix_T1 = \n");
printmatrix(matrix_T1, MATRIX_N, MATRIX_N);
matrix_mul(matrix_T1, matrix_A2, matrix_T2);
printf("matrix_T2 = \n");
printmatrix(matrix_T2, MATRIX_N, MATRIX_N);
matrix_mul(matrix_T2, matrix_A3, matrix_T3);
printf("matrix_T3 = \n");
printmatrix(matrix_T3, MATRIX_N, MATRIX_N);
matrix_mul(matrix_T3, matrix_A4, matrix_T4);
printf("matrix_T4 = \n");
printmatrix(matrix_T4, MATRIX_N, MATRIX_N);
matrix_mul(matrix_T4, matrix_A5, matrix_T5);
printf("matrix_T5 = \n");
printmatrix(matrix_T5, MATRIX_N, MATRIX_N);
matrix_mul(matrix_T5, matrix_A6, matrix_T6);
printf("matrix_T6 = \n");
printmatrix(matrix_T6, MATRIX_N, MATRIX_N);
//add();
//matrix_worldxyz[2][0] +=z_offset;
printf("\n----curent x, y, z-----\n%lf \n %lf\n %lf\n ",
matrix_T6[0][3], matrix_T6[1][3],
matrix_T6[2][3]+z_offset);
}
void initmatrix_A(param_t *p_table)
{//计算关节坐标矩阵 matrix A1--A6
calculate_matrix_A(matrix_A1, p_table+0);
printf("matrix_A1 = \n");
printmatrix(matrix_A1, MATRIX_N, MATRIX_N);
calculate_matrix_A(matrix_A2, p_table+1);
printf("matrix_A2 = \n");
printmatrix(matrix_A2, MATRIX_N, MATRIX_N);
calculate_matrix_A(matrix_A3, p_table+2);
printf("matrix_A3 = \n");
printmatrix(matrix_A3, MATRIX_N, MATRIX_N);
calculate_matrix_A(matrix_A4, p_table+3);
printf("matrix_A4 = \n");
printmatrix(matrix_A4, MATRIX_N, MATRIX_N);
calculate_matrix_A(matrix_A5, p_table+4);
printf("matrix_A5 = \n");
printmatrix(matrix_A5, MATRIX_N, MATRIX_N);
calculate_matrix_A(matrix_A6, p_table+5);
printf("matrix_A6 = \n");
printmatrix(matrix_A6, MATRIX_N, MATRIX_N);
}
void calculate_matrix_A(double matrix[MATRIX_N][MATRIX_N], param_t *p_param)
{//根据关节参数计算矩阵
double *pmatrix=(double *)matrix;
double value, var_c, var_s, angle_c, angle_s;
var_c = cos(p_param->joint_v);
IS_ZERO(var_c);
var_s = sin(p_param->joint_v);
IS_ZERO(var_s);
angle_c = cos(p_param->angle);
IS_ZERO(angle_c);
angle_s = sin(p_param->angle);
IS_ZERO(angle_s);
*pmatrix++ = var_c;
//value = -var_s * angle_c;
//IS_ZERO(value);
*pmatrix++ = -var_s * angle_c;
//value = var_s * angle_s;
//IS_ZERO(value);
*pmatrix++ = var_s * angle_s;
//value = p_param->length * var_c;
//IS_ZERO(value);
*pmatrix++ = p_param->length * var_c;
*pmatrix++ = var_s;
//value = var_c * angle_c;
//IS_ZERO(value);
*pmatrix++ = var_c * angle_c;
//value = -var_c *angle_s;
//IS_ZERO(value);
*pmatrix++ = -var_c *angle_s;
//value = p_param->length * var_s;
//IS_ZERO(value);
*pmatrix++ = p_param->length * var_s;
*pmatrix++ =0;
*pmatrix++ = angle_s;
*pmatrix++ = angle_c;
*pmatrix++ = p_param->d;
*pmatrix++ =0;
*pmatrix++ =0;
*pmatrix++ =0;
*pmatrix =1;
}
void initmatrix_tool(double toolx, double tooly, double toolz)
{
if(DEF_TOOLXYZ == 0){
matrix_toolxyz[2][0] =1;
}else{
matrix_toolxyz[0][0] =toolx;
matrix_toolxyz[1][0] =tooly;
matrix_toolxyz[2][0] =toolz;
{/* 初始化 toolrx, tooly, toolz */}
}
}
int matrix_mul(double matrix_a[MATRIX_N][MATRIX_N],
double matrix_b[MATRIX_N][MATRIX_N],
double matrix_result[MATRIX_N][MATRIX_N])
{
int i,j,k;
double sum;
double matrix_tmp[MATRIX_N][MATRIX_N]={0};
/*嵌套循环计算结果矩阵(m*p)的每个元素*/
for(i=0;ifor(j=0;j/*按照矩阵乘法的规则计算结果矩阵的i*j元素*/
sum=0;
for(k=0;kreturn 0;
}
int matrix_add(double matrix_a[MATRIX_N][MATRIX_N],
double matrix_b[MATRIX_N][MATRIX_N],
double matrix_sum[MATRIX_N][MATRIX_N], int m, int n)
{
int i,j;
double matrix_tmp[MATRIX_N][MATRIX_N]={0};
for(i=0; ifor(j=0; jreturn 0;
}
void matrix_copy(double matrix_src[MATRIX_N][MATRIX_N],
double matrix_des[MATRIX_N][MATRIX_N], int m, int n)
{
int i,j;
for(i=0; ifor(j=0; j