Covered Points Count题解
原文:欢迎浏览我的博客:http://www.fezhu.top/
题目
Covered Points Count
You are given n
segments on a coordinate line; each endpoint of every segment has integer coordinates. Some segments can degenerate to points. Segments can intersect with each other, be nested in each other or even coincide.
Your task is the following: for every k∈[1…n]
, calculate the number of points with integer coordinates such that the number of segments that cover these points equals k. A segment with endpoints li and ri covers point x if and only if li≤x≤ri.
Input
The first line of the input contains one integer n (1≤n≤2⋅105
) — the number of segments.
The next n
lines contain segments. The i-th line contains a pair of integers li,ri (0≤li≤ri≤1018) — the endpoints of the i-th segment.
Output
Print n space separated integers cnt1,cnt2,…,cntn, where cnti is equal to the number of points such that the number of segments that cover these points equals to i.
Examples
Input
3
0 3
1 3
3 8
Output
6 2 1
Input
3
1 3
2 4
5 7
Output
5 2 0
note
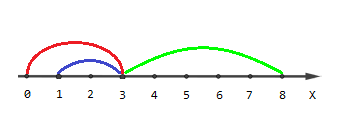
The picture describing the first example:
Points with coordinates [0,4,5,6,7,8] are covered by one segment, points [1,2] are covered by two segments and point [3]
is covered by three segments.
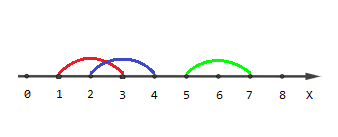
The picture describing the second example:
Points [1,4,5,6,7] are covered by one segment, points [2,3] are covered by two segments and there are no points covered by three segments.
分析
题目大意是给一个数n,接下来有n组输入,每次都给一个区间,区间上的每一个值都被覆盖一次,要你输出最后覆盖了1 2 3……次的数的数量
很典型的一道差分题,只不过这道题数据量很大(0≤li≤ri≤1018) ,开不了这么大的数组,但是数据量很小 (1≤n≤2⋅105),可以使用离散化,用一个数组储存每一次输入的左段点和右端点,然后把该数组进行排序去重,再定义一个新的差分数组进行差分操作,最后对差分数组求前缀和
code
#include
#include
#include
using namespace std;
typedef long long ll;
const int maxn=2e5+100;
struct node{
ll x,y;
}p[maxn];用一个数组储存端点值
ll a[maxn<<1],b[maxn<<1],c[maxn];//一个数组储存离散化后的值,一个数组储存差分的值,c数组用来存储最后结果
int main()
{
ios::sync_with_stdio(false);
int n,tail=0; cin>>n;
for(int i=1;i<=n;i++){
cin>>p[i].x>>p[i].y; //输入左端点和右端点
a[++tail]=p[i].x; //存入a数组用来离散化
a[++tail]=p[i].y+1;
}
sort(a+1,a+1+tail); //排序
int len=unique(a+1,a+1+tail)-a-1; //去重
for(int i=1;i<=n;i++){
int x=lower_bound(a+1,a+1+len,p[i].x)-a; //在a数组中找到每一组的左端点位置
int y=lower_bound(a+1,a+1+len,p[i].y+1)-a; //找右端点的下一个位置
b[x]++;b[y]--; //差分数组,左端点++,右端点的下一个位置--
}
for(int i=1;i<=len;i++){
b[i]+=b[i-1]; //求前缀和
c[b[i]]+=a[i+1]-a[i]; //c数组注意用long long,这里代表着从a[i]开始到a[i+1]都是被染色了b[i]次。
}
for(int i=1;i<=n;i++) printf("%lld%c",c[i],i==n?'\n':' ');
}
ok,结束