概率与统计分析练习题

1. 学习理解什么是极大似然估计

似然函数：设样本 X 有概率函数 \(f(x,\theta)\)，这里 \(\theta\) 为参数，在参数空间内取值。当固定 x 而把 \(f(x,\theta)\) 看成 \(\theta\) 的定义在参数空间内的函数时，它称为似然函数。

所以，概率函数和似然函数可以说是一回事，只是看法不同，前者是固定 \(\theta\) 而看成 x 在样本空间上的函数，后者则固定 x 而看成 \(\theta\) 在参数空间上的函数。不妨把参数 \(\theta\) 和样本 x 分别看成“原因”和“结果”，定了 \(\theta\) 的值，就完全确定了样本分布，也就定下了得到种种结果（x）的机会大小，这是从正面上。从反面看，当有了结果 x 时，我们问：当参数 \(\theta\) 取各种不同的值（原因）时，导出这个结果（x）的可能性有多大？这个问题的回答引出似然函数的概念，“似然”的字面意义就是“看起来像”，说仔细一些，就是：当我们有了结果 x 时，这个结果看来是由原因 \(\theta\) 而产生的可能性，与似然函数 \(f(x,\theta)\) 成比例。参数 \(\theta\) 有一定的值（虽然未知），并非事件或随机变量，无概率可言，于是就用“似然”这个词。

极大似然估计：若 \(\widehat{\theta}(X)\) 是一个统计量，满足条件

\[f(x,\widehat{\theta}(x))=\operatorname*{max}\limits_{\theta}f(x,\theta)\]

其中，x 在样本空间内取值，\(\theta\) 在参数空间内取值，则称 \(\widehat{\theta}(X)\) 是 \(\theta\) 的极大似然估计。若待估计函数是 \(g(\theta)\)，则称 \(g(\widehat{\theta}(X))\) 为极大似然估计。

\(\theta\) 的极大似然估计 \(\widehat{\theta}(X)\)，就是在已得样本 x 的情况下，似然性最大的那个 \(\theta\) 值。知道 x 自然不能唯一决定 \(\theta\)，取哪个值去估计 \(\theta\) 呢？要取那个“看起来最像”的值。

\(\widehat{\theta}\) 的确定要解一个极值问题，当 f 对 \(\theta\) 有连续的偏导数时，可通过使偏导等于 0 求出 \(\theta\)，验证它是一个极大值点，则它必是使 f 达到最大的点，即极大似然估计。在几个常见的重要例子中，这点不难验证。但在有些较复杂的场合，就无法用这种方法，就得回到定义。

2. 使用 Pandas 中的函数，下载上证综指过去 1 年的收盘数据，以此来计算日收益率序列，对这个数据画出直方图，计算这组数据的各个描述性统计量。

加载需要的包：

%matplotlib inline
import matplotlib.pyplot as plt
from scipy import stats
import numpy as np
import math
import pandas as pd
from datetime import datetime
from pandas_datareader import data, wb # 需要先安装 pandas_datareader
import seaborn as sns # 用于可视化\

sns.set(style="whitegrid")

下载指定时间段的数据：

start = datetime(2015, 6, 3)
end = datetime(2016, 6, 3)
sc = data.DataReader("000001.SS", 'yahoo', start, end) # 000001.SS 表示上证综指，返回 DataFrame
sc.head() # 纵轴是日期，横轴是开盘价、最高价、最低价、收盘价、成交量、复权收盘价。因上证综指并非具体某支股票，所以交易量为 0。

	Open	High	Low	Close	Volume	Adj Close
Date
2015-06-03	4909.98	4909.98	4909.98	4909.98	0	4909.98
2015-06-04	4947.10	4947.10	4947.10	4947.10	0	4947.10
2015-06-05	5023.10	5023.10	5023.10	5023.10	0	5023.10
2015-06-08	5131.88	5131.88	5131.88	5131.88	0	5131.88
2015-06-09	5113.53	5113.53	5113.53	5113.53	0	5113.53

去除不需要的数据列，只留收盘价数据。

sc = sc.drop('Open',axis=1)
sc = sc.drop('High',axis=1)
sc = sc.drop('Low',axis=1)
sc = sc.drop('Volume',axis=1)
sc = sc.drop('Adj Close',axis=1)
sc.head()

	Close
Date
2015-06-03	4909.98
2015-06-04	4947.10
2015-06-05	5023.10
2015-06-08	5131.88
2015-06-09	5113.53

计算日收益率序列。

sc["retRate"] = (sc.Close-sc.Close.shift(1))/sc.Close.shift(1) # 日收益率，当然在做实证时都用对数收益率
sc = sc.ix[1:]
sc.head()

	Close	retRate
Date
2015-06-04	4947.10	0.007560
2015-06-05	5023.10	0.015363
2015-06-08	5131.88	0.021656
2015-06-09	5113.53	-0.003576
2015-06-10	5106.04	-0.001465

pd.set_option('display.mpl_style', 'default')
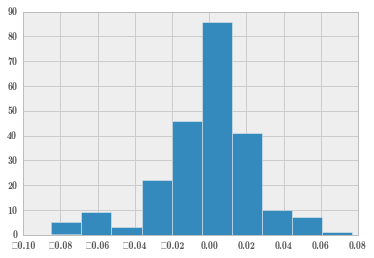
rrhist = sc.retRate.hist();

计算收盘价的各个描述性统计量。

sc.describe()

	Close	retRate
count	230.000000	230.000000
mean	3369.705696	-0.001901
std	559.895610	0.025486
min	2655.660000	-0.084907
25%	2940.407500	-0.012813
50%	3207.950000	0.000542
75%	3639.390000	0.012459
max	5166.350000	0.076940

3. 对上述收益率数据，使用参数方法和非参数方法估计其概率密度函数。参数方法选择正态分布和对数正态分布两种假设。基于上述三种方法分别计算收益率小于 0 的概率。

在金融学中，一般股票价格趋向对数正态分布，其收益率趋向正态分布。

正态分布

收益率趋向正态分布。

一般对正态性的考察可以通过直方图进行，当数据量较少时甚至可以直接观察数据。通过上面的直方图，可以看出日收益率是符合正态分布的。

要求该正态分布的概率密度函数，只需求出期望和方差即可。其实就是从上面的收益率样本数据中估计出整体的期望和方差。

我们使用总体分布均值和方差的无偏估计，即样本均值和样本方差。

设 \(X_{1},...,X_{n}\) 是从正态总体 \(N(\mu,\sigma^2)\) 中抽出的样本，则

样本均值：

\[\bar{X}=\frac{\sum^{n}_{i=1}X_{i}}{n}\]

样本方差：

\[S^{2}=\frac{\sum^{n}_{i=1}(X_{i}-\bar{X})^{2}}{n-1}\]

mu = sc.retRate.mean()
var = ((sc.retRate-mu)**2).sum()/(sc.retRate.count()-1)
print mu
print var

-0.0019014427158
0.000649550355968

把 mu 和 var 作为期望和方差代入正态分布密度函数即可。

sigma = math.sqrt(var);

X = stats.norm(mu, sigma) # 定义一个正态分布，期望是 mu，标准差是 sigma

fig, ax = plt.subplots(figsize=(8, 3))

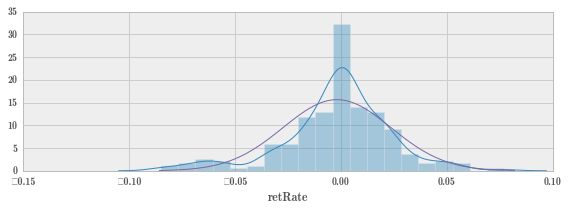
sns.distplot(sc.retRate, ax=ax) # 画真实数据的图形，蓝色线，分布其实是以 0.8 为期望值
x = np.linspace(*X.interval(0.999), num=100)
ax.plot(x, X.pdf(x)) # 理论上值 mu=1，绿色的线

fig.tight_layout();

/root/anaconda2/lib/python2.7/site-packages/matplotlib/font_manager.py:1298: UserWarning: findfont: Could not match :family=Bitstream Vera Sans:style=normal:variant=normal:weight=400:stretch=normal:size=large. Returning /usr/share/matplotlib/mpl-data/fonts/ttf/cmb10.ttf
  UserWarning)

注意到上图中的概率密度函数在一大片区域的值都大于 1，开始我还以为 X.pdf 函数出错了，反复检查几次，又手写了求正态分布值的函数验证了下，确认没有问题，才想起连续型随机变量的密度函数的其中一个性质是曲线下的面积为 1，而不是说密度函数值不能大于 1。

\[\int_{-\infty}^{\infty}f(x)dx=1\]

def normpdf(x, mu, sigma):
    u = (x-mu)/np.abs(sigma)
    y = (1/(np.sqrt(2*np.pi)*abs(sigma)))*np.exp(-u*u/2)
    return y

print normpdf(-0.0019014427158, mu, sigma)
print X.pdf(-0.0019014427158)

15.6532187074
15.6532187074

计算日收益率小于 0 的概率，其实就是求概率累积分布函数等于 0 时的值。

print X.cdf(0) # 计算日收益率小于 0 的概率

0.529736110272

参数方法选择正态分布假设时，收益率小于 0 的概率为 0.53。

对数正态分布

股票价格趋向对数正态分布。

如果 Close 服从对数正态分布，则 log(Close) 服从正态分布，我们先求出 log(Close) 的期望和方差。

sc["logClose"] = np.log(sc["Close"]) # 日收益率，当然在做实证时都用对数收益率
sc.head()

	Close	retRate	logClose
Date
2015-06-04	4947.10	0.007560	8.506557
2015-06-05	5023.10	0.015363	8.521803
2015-06-08	5131.88	0.021656	8.543227
2015-06-09	5113.53	-0.003576	8.539645
2015-06-10	5106.04	-0.001465	8.538179

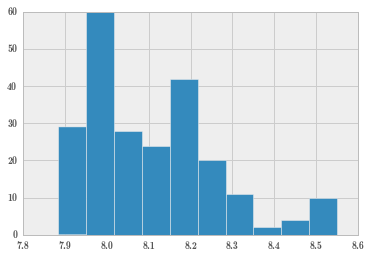
sc.logClose.hist();

再求符合对数正态分布的 Close 的期望和方差。

logClosemu = sc.logClose.mean()
logClosevar = ((sc.logClose-logClosemu)**2).sum()/(sc.logClose.count()-1)
Closemu = np.e**(logClosemu+logClosevar/2)
Closevar = np.e**(2*mu+logClosevar)*(np.e**(logClosevar**2)-1)
print logClosemu
print logClosevar

8.11018944858
0.0237394048181

股票价格服从期望为 Closemu，方差为 Closevar 的对数正态分布。

logsample = stats.norm.rvs(loc=logClosemu, scale=logClosevar, size=1000) # logsample ~ N(mu=10, sigma=3)

非参数估计

kde = stats.kde.gaussian_kde(sc.retRate) # 高斯核函数，kde 是核函数密度估计，核分布是种非参数估计方法
kde_low_bw = stats.kde.gaussian_kde(sc.retRate, bw_method=0.25) # bw_method 为窗宽参数，该值越小，就越受到数据本身的影响
minValue = sc.retRate.min()
maxValue = sc.retRate.max()
x = np.linspace(minValue, maxValue, 100)

fig, ax = plt.subplots(figsize=(8, 3))

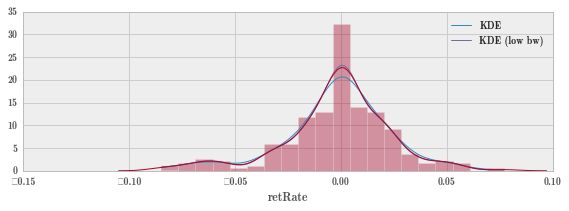
plt.plot(x, kde(x), label="KDE");
plt.plot(x, kde_low_bw(x), label="KDE (low bw)");
plt.legend();

sns.distplot(sc.retRate, ax=ax) # 画真实数据的图形，红色线

fig.tight_layout()

上图可以看到，高斯核函数的蓝色曲线跟实际数据拟合的还不错。

KDE 没有累积分布函数，我们可以手工计算。

def _kde_cdf(x):
    return kde.integrate_box_1d(-np.inf, x) # 得到经验分布的累积分布图形

print _kde_cdf(0) # 计算日收益率小于 0 的概率

0.499018774421

使用非参数估计方法，日收益率小于 0 的概率为 0.5。

4. 使用 Pandas 中的函数，下载你感兴趣的任意两支股票的数据，计算日收益率序列，使用假设检验来判断这两支股票的平均收益率是否有差别。

两样本 t 检验，对两个正态总体均值差的检验。这里比较的是 58 同城和百度的股票。

先下载数据，并预处理，计算出日收益率序列。

start = datetime(2015, 6, 3)
end = datetime(2016, 6, 3)
wuba = data.DataReader("WUBA", 'yahoo', start, end) # WUBA 表示 58 同城，返回 DataFrame
wuba.head() # 纵轴是日期，横轴是开盘价、最高价、最低价、收盘价、成交量、复权收盘价。因上证综指并非具体某支股票，所以交易量为 0。

wuba = wuba.drop('Open',axis=1)
wuba = wuba.drop('High',axis=1)
wuba = wuba.drop('Low',axis=1)
wuba = wuba.drop('Volume',axis=1)
wuba = wuba.drop('Adj Close',axis=1)

wuba["retRate"] = (wuba.Close-wuba.Close.shift(1))/wuba.Close.shift(1) # 日收益率，当然在做实证时都用对数收益率
wuba = wuba.ix[1:]
wuba.head()

	Close	retRate
Date
2015-06-04	76.400002	0.003151
2015-06-05	80.419998	0.052618
2015-06-08	81.800003	0.017160
2015-06-09	81.330002	-0.005746
2015-06-10	78.940002	-0.029386

start = datetime(2015, 6, 3)
end = datetime(2016, 6, 3)
baidu = data.DataReader("BIDU", 'yahoo', start, end) # BIDU 表示百度，返回 DataFrame
baidu.head() # 纵轴是日期，横轴是开盘价、最高价、最低价、收盘价、成交量、复权收盘价。因上证综指并非具体某支股票，所以交易量为 0。

baidu = baidu.drop('Open',axis=1)
baidu = baidu.drop('High',axis=1)
baidu = baidu.drop('Low',axis=1)
baidu = baidu.drop('Volume',axis=1)
baidu = baidu.drop('Adj Close',axis=1)

baidu["retRate"] = (baidu.Close-baidu.Close.shift(1))/baidu.Close.shift(1) # 日收益率，当然在做实证时都用对数收益率
baidu = baidu.ix[1:]
baidu.head()

	Close	retRate
Date
2015-06-04	204.330002	0.002207
2015-06-05	205.889999	0.007635
2015-06-08	203.149994	-0.013308
2015-06-09	202.559998	-0.002904
2015-06-10	204.630005	0.010219

然后把 58 同城和百度的日收益率数据传入 t 检验函数，求出 p 值。

t, p = stats.ttest_ind(wuba.retRate, baidu.retRate) # 两样本 T 检验
print t
print p # p 值太小，可以拒绝原假设

-0.370593217437
0.711096236413

p 值远远大于 0.05，说明两支股票的平均收益率一样，没啥差别。

转载于:https://www.cnblogs.com/NaughtyBaby/p/5568685.html