通配符匹配（Wildcard Matching）与正则表达式匹配（Regular Expression Matching）解法解析

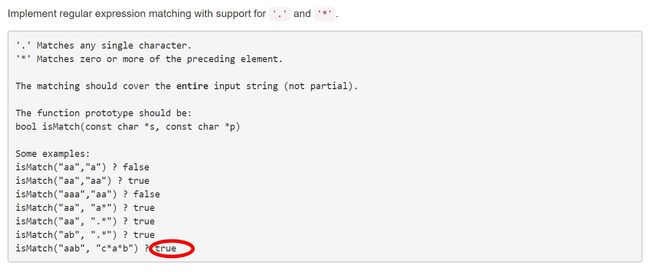
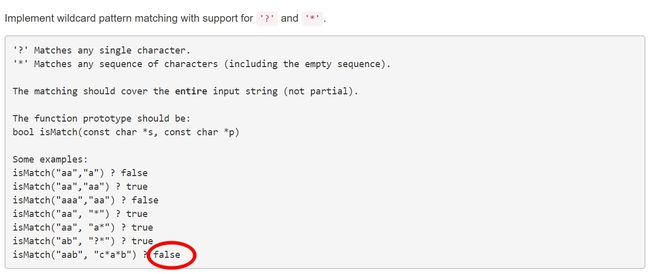
    编程题，通配符匹配（Wildcard Matching）与正则表达式匹配（Regular Expression Matching）在字符串匹配中比较常见也比较重要，在leetcode中就有这么两道题，极其相似，见下图（注意图中红圆圈地方的区别）：

正则表达式匹配（Regular Expression Matching）（注意："a* "可表示  " "、"a"、"aa"……）

通配符匹配（Wildcard Matching）

    （题意很好理解，不解释）

    这两个问题如此一致，是不是解法也一致？答案：是的，他们是同一种“动态规划”问题，而这两个问题的解法的关键是理解“要规划的对象（最优子结构）是什么”。“动态规划”思想是，先求解子子问题，再利用子子问题的解求得子问题的解，最终求得原问题的解。“动态规划”与“分治策略”，都是将规模为n的原问题，转换为求解形式完全一样的、但规模更小的、并可以独立求解的，子子问题来解决。而“动态规划”的优势在于 它可采用“自底向上”的求解顺序，避免重复计算相同的子子问题，效率更高。

    这两道题还有一个共同的特点，就是 “解”（即匹配成功）不唯一，我们需要找到其中一个解（输出TRUE，否则输出FALSE）。下面以正则表达式匹配为例讲解“动态规划”的解决方案，“通配符匹配”比“正则表达式匹配”简单些。

   解题思路：

    1.刻画“最优子结构”。令一个二维矩阵 vec[i][j] 来表示字符串 s前 i 个字符  和  字符串 p前 j 个字符  的匹配问题。vec[i][j] == 1 表示匹配成功，否则失败。原问题与子问题，都可以表示成这种 vec[i][j] 子结构。假设字符串 s 和 p 的长度分别为 ls 和 lp ，则 vec[ls][lp] == 1 表示原问题有解（匹配成功），否则无解（匹配失败）。

    针对 vec[i][j] 原问题（或子问题），我们需要先求解一个或两个子问题（或子子问题），当 p[j] != ' * ' 时，求解 vec[i-1][j-1] 这个子子问题；当 p[j] == ' * ' 时，求解 vec[i][j-1] 子子问题 或 求解 vec[i-1][j] 子子问题。即，我们必须依赖上面3个子子问题的情况，来求出 vec[i][j] 问题的解。

    通过 vec[i][j] ，我们发现“原问题（子问题）的解依赖其子问题（子子问题）的解”，子问题有解时 原问题才会有解，即满足“最优子结构”特性。

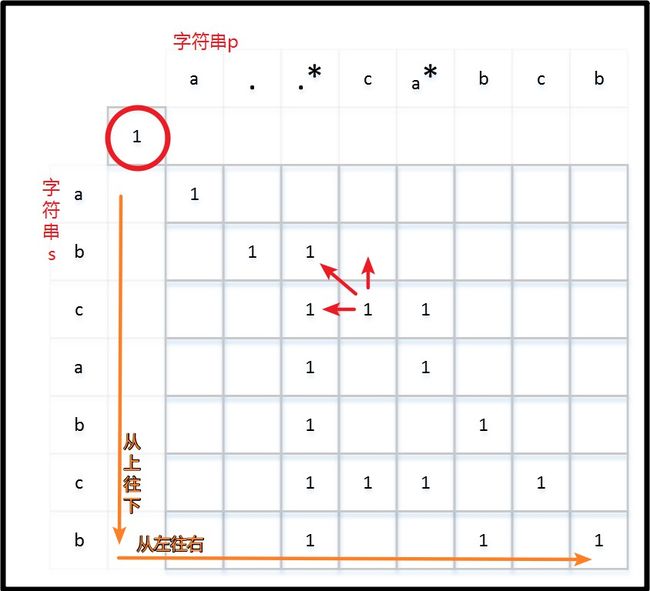
    2.“自底向上”求解。先求解最小的子子问题 vec[1][1]，再不断求解子问题vec[i][j]。很显然，如果当 j == k < lp 时， 所有的 vec[i][k] == 0，则 后面所有 j > k的子问题 vec[i][j] == 0，从而原问题无解。于是我们采用“从上往下  从左往右”的顺序求解每个子问题vec[i][j]，如下图。

红色箭头表示当前子问题 vec[i][j] 的子子问题 vec[i-1][j-1]、vec[i][j-1]、vec[i-1][j]。红圆圈为vec[0][0]的“前0个字符匹配”的特殊情况，显然匹配成功  ==1。

下面是“正则表达式匹配”问题C++代码：

bool isMatch(string s, string p) {
	s += '#';reverse(s.begin(), s.end());// 添加特殊的结尾标记符 # ，然后反转，这里是为了后面处理方便
	p += '#';reverse(p.begin(), p.end());
	int ls = s.size(), lp = p.size();
	vector > sp(ls, vector(lp, false));// 最优子结构 sp[][]，全部初始化为 false
	
	sp[0][0] = true;// 特殊位置，前 0 个字符匹配成功
	int pos = 0;
	bool pos_b = true;
	for (int j = 1, i = pos; j < lp && pos_b; j++)// 外循环 从左往右
		if (p[j] == '*')
			for (i = pos, j++; i < ls; i++)// 内循环 从上往下
				sp[i][j] = sp[i][j - 2] || i > 0 && (p[j] == '.' || s[i] == p[j]) && sp[i - 1][j];// 依赖 子子问题 sp[i][j - 1] 和 子子问题 sp[i - 1][j]
		else {
			pos_b = false;
			for (i = ++pos; i < ls; i++){// 内循环 从上往下
				sp[i][j] = sp[i - 1][j - 1] && (p[j] == '.' || s[i] == p[j]);// 依赖 子子问题 sp[i - 1][j - 1]
				if (!pos_b && sp[i][j]) {pos_b = true;pos = i;}
				else if (!pos_b) ++pos;
			}
		}
	return sp[ls - 1][lp - 1];// 返回原问题的解
}

“通配符匹配”比“正则表达式匹配”简单些，只需要将上面的代码稍稍改改就可以解决问题，原理一样。

代码如下：

bool isMatch(string s, string p) {
	s += '#';reverse(s.begin(), s.end());
	p += '#';reverse(p.begin(), p.end());
	int ls = s.size(), lp = p.size();
	vector > sp(ls, vector(lp, false));
	
	sp[0][0] = true;
	int pos = 0;
	bool pos_b = true;
	for (int j = 1, i = pos; j < lp && pos_b; j++)
		if (p[j] == '*')
			for (i = pos; i < ls; i++)// 修改
				sp[i][j] = true;// 修改
		else {
			pos_b = false;
			for (i = ++pos; i < ls; i++){
				sp[i][j] = sp[i - 1][j - 1] && (p[j] == '?' || s[i] == p[j]);// 修改 “?”
				if (!pos_b && sp[i][j]) {pos_b = true;pos = i;}
				else if (!pos_b) ++pos;
			}
		}
	return sp[ls - 1][lp - 1];   
}