人工智能-高等数学之微积分篇

高等数学之微积分篇

接着上一篇《人工智能-高等数学之导数篇》，继续学习汇总微积分的知识，微分和导数外形很相似，导致有时候傻傻的分不清楚，在查找无数资料之后我找到了一个能够被理解的说法，导数是函数图像在某一点处的斜率，是纵坐标增量（Δy）和横坐标增量（Δx）在Δx–>0时的比值。而微分是指函数图像在某一点处的切线在横坐标取得增量Δx以后，纵坐标取得的增量，一般表示为dy。积分是微分的逆运算，即知道了函数的导函数，反求原函数。还有一种简要的概括说法，导数描述的是函数在一点处的变化快慢的趋势，是一个变化的速率，微分描述的是函数从一点（移动一个无穷小量）到另一点的变化幅度，是一个变化的量。

1. 微分的定义

数学定义：设函数$y=f(x)$在某区间内有定义，$x_0$及$x_0+\Delta x$在这区间内，如果增量$\Delta y=f(x_0+\Delta x)-f(x_0)$可以表示为$\Delta y=A\Delta x+o(\Delta x)$，其中A是不依赖于$\Delta x$的常数，那么称函数$y=f(x)$在点$x_0$是可微的，而$A\Delta x$叫做函数$y=f(x)$在点$x_0$相应于自变量增量$\Delta x$的微分，记作dy，即$dy=A\Delta x$

2. 微分系数和导函数

设$f(x)$是定义在区间$I$上的函数，如果a是区间$I$内的一点，那么$\frac{f(x)-f(a)}{x-a}$是定义在区间$I$内除了a以外的x点上的函数，此时如果存在极限：
$$\underset{x\to a}{\lim }\frac{f(x)-f(a)}{x-a}，$$，那么就称$f(x)$在点a处可微，或者称在x=a处可微，并称此极限为函数$f(x)$在点a处的微分系数，记为$f^{\prime }(a)$
$$f^{\prime }(a)=\underset{x\to a}{\lim }\frac{f(x)-f(a)}{x-a}，$$
当函数$f(x)$在所属区间内的任意点$x$处均可微时，则称函数$f(x)$可微，或称$f(x)$关于x可微。此时$f^{\prime }(x)$也是定义在区间$I$上的关于x的函数。称$f^{\prime }(x)$为函数$f(x)$的导函数，求函数$f(x)$的导函数$f^{\prime }(x)$，称为对函数$f(x)$进行微分，或函数$f(x)$关于x进行微分。
所以在数学表达上，如果对于函数$y=f(x)$，存在$dy=f^{\prime }(x)dx$，称$dy$是$y$的微分或$f(x)$的微分。
莱布尼茨对导数的记法：

$f^{\prime }(x)=\frac{dy}{dx}\Rightarrow dy\Rightarrow f^{\prime }(x)dx$，

从中我们可以看出，导数是$y$的微分与$x$微分的比值，所以导数也叫做微商（两个微分的商）

给出原始公式，如下：
$$\frac{dy}{dx}=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$

3. 初等函数的微分公式

导数公式	微分公式
$(nx{)}^{\prime }=n,n\in R$	$d(nx)=ndx,n\in R$
$(x^n{)}^{\prime }=n{x}^{n-1},n\in R$	$d(x^n)=n{x}^{n-1}dx,n\in R$
$(\sin x{)}^{\prime }=\cos x$	$d(\sin x)=\cos xdx$
$(\cos x{)}^{\prime }=-\sin x$	$d(\cos x)=-\sin xdx$
$(a^x{)}^{\prime }=a^x\ln a$	$d(a^x)=a^x\ln adx$

4. 函数和差积商的微分法则

和差积商的 求导法则	和差积商的 微分法则
$(u\pm v{)}^{\prime }=u^{\prime }\pm v^{\prime }$	$d(u\pm v)=du\pm dv$
$(uv{)}^{\prime }=u^{\prime }v+u{v}^{\prime }$	$d(uv)=duv+udv$
$(Cv{)}^{\prime }=C{v}^{\prime }$	$d(Cv)=Cdv$
$(\frac{u}{v}{)}^{\prime }=\frac{(u^{\prime }v-u{v}^{\prime })}{v^2}$	$d(\frac{u}{v})=\frac{(duv-udv)}{v^2}$

5. 不定积分与定积分

根据牛顿-莱布尼茨公式，许多函数的定积分的计算就可以简便地通过求不定积分来进行。这里要注意不定积分与定积分之间的关系：定积分是一个数，而不定积分是一个表达式，它们仅仅是数学上有一个计算关系。一个函数，可以存在不定积分，而不存在定积分，也可以存在定积分，而没有不定积分。

5.1 不定积分

如果有一个关于x的函数G(x),g(x)是G(x)的导数，即，$G^{\prime }(x)=g(x)$，则式子 $G(x)=\int g(x)dx$ 称为g(x)dx的不定积分，其中g(x)dx是G(x)的微分，对微分的积分是原函数，所以微分和积分互为反函数。所以求解不定积分的方法就是将导数逆推。例如：
$\int \sin xdx=？$，如果 $G(x)=-\cos x$，则 $G^{\prime }(x)=\sin x$，所以 $\int \sin xdx=-\cos x+C$，其中C是一个任意常数，因为C不确定大小，它是不定的，不是一个确切的函数，所以才叫做不定积分。

5.2 定积分

数学定义：设函数f(x)在[a,b]上有界，在[a,b]中任意插入若干个分点$a<x_0<x_1<x_2<\cdots <x_{n-1}<x_n=b$，把区间[a,b]分成n个小区间 $[x_0,x_1],[x_1,x_2],\cdots ,[x_{n-1},x_n]$ ，各个小区间的长度依次为 $\Delta x_1=x_1-x_0,\Delta x_2=x_2-x_1,\cdots ,\Delta x_n=x_n-x_{n-1}$，在每个小区间$[x_{i-1},x_i]$ 上取任意一点 $\xi (x_{i-1}\le {\xi }_i\le x_i)$，作函数值$f(\xi )$ 与小区间长度 $\Delta x_i$ 的乘积$f(\xi )\Delta x_i，(i=1,2,3,\cdots ,n)$，并作出和
$$S=\sum _{i=1}^{n}f({\xi }_i)\Delta x_i\text{\hspace{1em}(1)}$$
记$\lambda =max\{\Delta x_1,\Delta x_2,\cdots ,\Delta x_n\}$，如果不论对[a,b]怎样划分，也不论在小区间 $[x_{i-1},x_i]$ 上的点 $\xi$ 怎样选取，只要当 $\lambda \to 0$ 时，和S总趋于确定的极限$I$，那么称这个极限$I$ 为函数 $f(x)$ 在区间 [a,b] 上的定积分，简称积分，记作 ${\int }_a^{b}f(x)dx$，即

$${\int }_a^{b}f(x)dx=I=\underset{\lambda \to 0}{\lim }\sum _{i=1}^{n}f({\xi }_i)\Delta x_i\text{\hspace{1em}(2)}$$
其中f(x)叫做被积函数，f(x)dx叫做被积表达式，x 叫做积分变量，a叫做积分下限，b叫做积分上限，[a,b] 叫做积分区间。

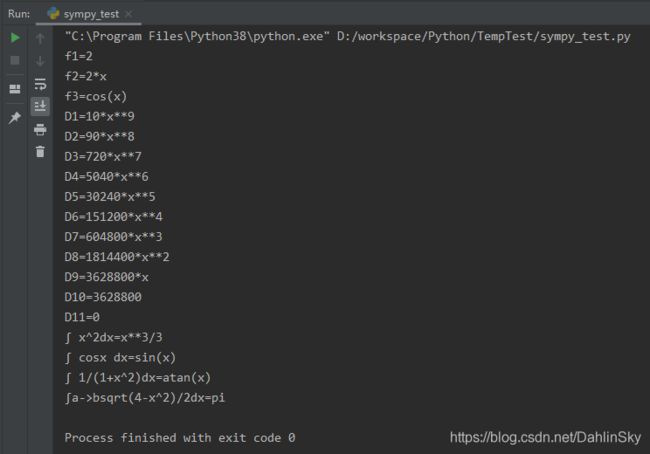
6. python计算代码

手算太累了，还是交给Python吧，它擅长这个。

import sympy as sp

if __name__ == '__main__':

    # 定义自变量x,表示对x求导
    x = sp.symbols('x', real=True)
    f1 = 2 * x + 1
    derivative = sp.diff(f1, x)
    print('f1=%s' % derivative)
    f2 = x ** 2 + 4
    derivative = sp.diff(f2, x)
    print('f2=%s' % derivative)
    f3 = sp.sin(x)
    derivative = sp.diff(f3, x)
    print('f3=%s' % derivative)
    # 求高阶导数
    f4 = x ** 10
    for n in range(1, 12):
        # 计算n阶导数
        D = sp.diff(f4, x, n)
        print('D%d=%s' % (n, D))

    # 定义被积函数
    fx1 = x ** 2
    fx2 = sp.cos(x)
    fx3 = 1 / (1 + x ** 2)

    # 计算不定积分
    r1 = sp.integrate(fx1, x)
    r2 = sp.integrate(fx2, x)
    r3 = sp.integrate(fx3, x)
    print('∫ x^2dx=%s' % r1)
    print('∫ cosx dx=%s' % r2)
    print('∫ 1/(1+x^2)dx=%s' % r3)

    # 求解定积分
    fx4 = sp.sqrt(4 - x**2) / 2
    r4 = sp.integrate(fx4, (x, -2, 2))
    print('∫a->bsqrt(4-x^2)/2dx=%s' % r4)

运行结果：