程序设计与算法（二）算法基础课--1、枚举 python实现

程序设计与算法（二）算法基础课–1、枚举 python实现
课程源自mooc网，北京大学郭炜老师的课程，这里只是作为课程笔记分享，原课程使用c++实现，这里用python实现。
课件：链接:https://pan.baidu.com/s/1Ld2gNhwILc6vDZdiNgFToQ 密码:1p7b
视频请见mooc网：程序设计与算法（二）算法基础

---

第一节课枚举一共有4道例题。

（1）完美立方（2）生理周期（3）假币问题（4）熄灯问题。

前两题都是非常规矩的枚举题，思考难度和代码难度都不大，后两题都比较复杂。

---

题1:完美立方

形如a3= b3 + c3 + d3的等式被称为完美立方等式。例如 123= 63 + 83 + 103 。编写一个程序，对任给的正整数N (N≤100)，寻找所有的四元组(a, b, c, d)，使得a3 = b3 + c3 + d3，其中a,b,c,d 大于 1, 小于等于N，且b<=c<=d。
输入：一个正整数N (N≤100)。
输出：每行输出一个完美立方。输出格式为:Cube = a, Triple = (b,c,d) 其中a,b,c,d所在位置分别用实际求出四元组值代入。请按照a的值，从小到大依次输出。当两个完美立方 等式中a的值相同，则b值小的优先输出、仍相同 则c值小的优先输出、再相同则d值小的先输出。

样例输入：24

样例输出：

Cube = 6, Triple = (3,4,5)
Cube = 12, Triple = (6,8,10)
Cube = 18, Triple = (2,12,16)
Cube = 18, Triple = (9,12,15)
Cube = 19, Triple = (3,10,18)
Cube = 20, Triple = (7,14,17)
Cube = 24, Triple = (12,16,20)

解题思路：

题目其实隐藏了遍历顺序，先a，b，c，d
并且：$a\in [2,N],b\in [2,a-1],c\in [b,a-1],d\in [c,a-1]$
所以：

python代码：

def perfect_cube(N):
    cube_list = []
    for a in range(2,N+1):
        for b in range(2,a):
            for c in range(b,a):
                for d in range(c,a):
                    if a**3 == (b**3+c**3+d**3):
                        cube_list.append((a,b,c,d))
    for t in cube_list:
        a,b,c,d = t[0],t[1],t[2],t[3]
        print('Cube=%d,Triple=(%d,%d,%d)'%(a,b,c,d))
    return cube_list
cube_list = perfect_cube(24)!

结果：

题2:生理周期

人有体力、情商、智商的高峰日子，它们分别每隔 23天、28天和33天出现一次。对于每个人，我们想 知道何时三个高峰落在同一天。给定三个高峰出现 的日子p,e和i(不一定是第一次高峰出现的日子), 再给定另一个指定的日子d，你的任务是输出日子d 之后，下一次三个高峰落在同一天的日子(用距离d 的天数表示)。例如:给定日子为10，下次出现三 个高峰同一天的日子是12，则输出2。
输入: 四个整数:p, e, i和d。 p, e, i分别表示体力、情感和智力高峰出现的日子。d是给定的日子，可能小于p, e或 i。所有给 定日子是非负的并且小于或等于365，所求的日子小于或等于 21252。
输出: 从给定日子起，下一次三个高峰同一天的日子(距离给定日子的天数)。

解题思路：

（1）首先分析数字21252。是23，28和33的最小公倍数。所以说这里不涉及多个日期，所有的只涉及唯一值。所以不需要选择公倍数的日期，不涉及周期问题。
（2）下一步就是开始遍历，即那一天满足(k – p)%23 == 0 && (k – e)%28 == 0 && (k-i)%33 == 0.
（3）跳着遍历，先找到第一个符合(k – p)%23 == 0的日子，然后加+23，寻找哪一天(k – e)%28 == 0 ，然后跳23和28的最小公倍数天，然后判断哪一天还符合(k-i)%33 == 0。
方案二：（3）如果不想找两个数字的最小公倍数，就直接遍历也可以。

python代码：

最小公倍数代码：

def gcd(a,b): #stein 算法
    if b>a:
        a,b = b,a 
    if b==0:
        return a 
    if b==a:
        return a 
    if a%2 ==0 and b%2 ==0:
        return 2*(gcd(a/2,b/2))
    if a%2 ==0:
        return gcd(a/2,b)
    if b%2 == 0: 
         return gcd(a,b/2)
    return gcd((a+b)/2,(a-b)/2)

def lcm(a,b):
    return a*b/gcd(a,b)

生理周期代码：

def life_circle(p,e,i,d):
    cycle_p = 23 
    cycle_e = 28 
    cycle_i = 33
    cycle_pe = lcm(cycle_e,cycle_p)
    d0=d+1
    while d0 <=21252:
        if (d0-p)%cycle_p ==0: 
            if (d0-e)%cycle_e == 0:
                if (d0-i)%cycle_i == 0:
                    return d0-d
                else:
                    d0+= cycle_pe
            else:
                d0+=cycle_p
        else:
            d0+=1
    return -1
print('the next triple peak occurs in %d days!'%(life_circle(5,20,34,325)))

结果：

题3: 假币问题

有12枚硬币。其中有11枚真币和1枚假币。假币和真币重量不同，但不知道假币比真币轻还是重。现在， 用一架天平称了这些币三次，告诉你称的结果，请你找出假币并且确定假币是轻是重(数据保证一定能找出来)。
输入:
第一行是测试数据组数。
每组数据有三行，每行表示一次称量的结果。银币标号为 A-L。每次称量的结果用三个以空格隔开的字符串表示: 天平左边放置的硬币 天平右边放置的硬币 平衡状态。其中平衡状态用’‘up’’, ‘‘down’’, 或 '‘even’'表示, 分别为右端高、右端低和平衡。天平左右的硬币数总是相等的。
输出:
输出哪一个标号的银币是假币，并说明它比真币轻还是重。

解题思路

（1）这道题目的不同之处在于，不是让我们想办法去称量出来哪一个是假币，而是他提供可以找到假币的称量方式我们只需要根据结果找出来哪一个为假币即可。
（2）输入左右一定相等，一共12枚硬币，所以每次称量左右单边长度最大为6，最小为1。
（3）up为右端高，即右边轻，down，右端重，even，一样重。

---

老师给的解决方案：

对于每一枚硬币先假设它是轻的，看这样是否符合称 量结果。如果符合，问题即解决。如果不符合，就假 设它是重的，看是否符合称量结果。把所有硬币都试一遍，一定能找到特殊硬币

老师的方案的尝试的次数为12*2=24次。

---

这里我们可以换一种思路思考，根据题目的特殊性，一共12枚硬币，而且只有假币的质量不同，但是不知道假币的质量是轻还是重。
换句话说：如果称量结果为even，现在出现的所有硬币一定都是真币，如果称量结果为up或者down，出现的硬币中一定有假币。
可以归纳为：
（1）结果只有even，没有称量的那一枚硬币为假，但是这样的话无法知道轻重，所以肯定不成立。
（2）结果有even和up/down：我们可以把所有称量过的硬币作为一个集合，排除掉所有出现在even中的硬币，然后去检验剩余的硬币是否成立。

python代码

def weight_coins(inputs):
    correct_list = [] #肯定正确的硬币列表
    suspect_list = [] #有怀疑的硬币列表
    for i in range(3):
        inp = inputs[i]
        left,right,result = inp.split('\t')       
        if result == 'even':
            #结果为even的所有硬币一定为真
            correct_list.extend(list(left))
            correct_list.extend(list(right))
        else:
            #结果不为even的硬币有怀疑
            suspect_list.extend(list(left))
            suspect_list.extend(list(right))
    suspect_list = list(set(suspect_list)-set(correct_list))#将有怀疑的硬币排除肯定正确的硬币
    #对有怀疑的硬币遍历
    for coin in suspect_list:
        #对轻重进行遍历
        for state in iter(['light','heavy']):
            flag = True #判断三个结果是否正确，有一次违背就是False
            for i in range(3):
                inp = inputs[i]
                left,right,result = inp.split('\t')
                if result == 'even':
                    if coin in left or coin in right:
                        flag = False
                        break
                elif result == 'up':
                    if coin not in right:
                        flag = False
                        break
                else:
                    if coin not in left:
                        flag = False
                        break
            if flag:
                artificial_coin = coin 
                state = state
                return artificial_coin,state
            
inputs = ['ABCD\tEFGH\teven','ABCI\tEFJK\tup','ABIJ\tEFGH\teven']
artificial_coin,state = weight_coins(inputs)
print('%s is the counterfeit coin and it is %s'%(artificial_coin,state))

题4: 熄灯问题

有一个由按钮组成的矩阵, 其中每行有6个按钮, 共5行,每个按钮的位置上有一盏灯, 当按下一个按钮后, 该按钮以及周围位置(上边, 下边, 左 边, 右边)的灯都会改变状态, 如果灯原来是点亮的, 就会被熄灭 ;如果灯原来是熄灭的, 则会被点亮。
（1）在矩阵角上的按钮改变3盏灯的状态（2）在矩阵边上的按钮改变4盏灯的状态 （3） 其他的按钮改变5盏灯的状态

与一盏灯毗邻的多个按钮被按下时,一个操作会抵消另一次操作的结果,给定矩阵中每盏灯的初始状态，求一种按按钮方案，使得所有 的灯都熄灭
输入:
– 第一行是一个正整数N, 表示需要解决的案例数
– 每个案例由5行组成, 每一行包括6个数字
– 这些数字以空格隔开, 可以是0或1
– 0 表示灯的初始状态是熄灭的
– 1 表示灯的初始状态是点亮的
输出：
– 对每个案例, 首先输出一行,输出字符串 “PUZZLE #m”, 其中m是该案例的序 号
– 接着按照该案例的输入格式输出5行
• 1 表示需要把对应的按钮按下
• 0 表示不需要按对应的按钮
• 每个数字以一个空格隔开

解题思路

（1）题目隐藏信息：第2次按下同一个按钮时, 将抵消第1次按下时所产生的结果。所以只有按或者不按两个选择，不用记录次数。
（2）各个按钮被按下的顺序对最终的结果没有影响。
（3）遍历：

• 可以对每个灯的状态进行开关遍历，看是否成立，需要遍历2³⁰次。次数太多，会超时。
  老师的改进思路：

如果存在某个局部, 一旦这个局部的状态被确定,那么剩余其他部分的状态只能是确定的一种, 或者不多的种, 那么就只需枚举这个局部的状态即可.

• 经过观察, 发现第1行就是这样的一个 “局部”,因为第1行的各开关状态确定的情况下, 这些开关作用过后, 将 导致第1行某些灯是亮的, 某些灯是灭的。要熄灭第1行某个亮着的灯(假设位于第i列), 那么唯一的办法就 是按下第2行第i列的开关。为了熄灭第2行的灯, 第3行的合理开关状态就也是唯一的。
  推算出最后一行的开关状态, 然后看看最后一行的开关起作用后, 最后一行的所有灯是否都熄灭:
  • 如果是,那么A就是一个解的状态
  • 如果不是,那么A不是解的状态,第1行换个状态重新试试

只需枚举第1行的状态, 状态数是2⁶ = 64

Q: 有没有状态数更少的做法?
AS: 枚举第一列, 状态数是2⁵ = 32

（4）高效的存储和遍历方案：

• 一个char的变量类型一个位有8个bit，这里只需要用6个，所以只需要5个char的数组，就可以存储灯的状态。
• 开关起作用，就是从0->1 1>0,即使用位运算
• 枚举的时候的快捷方法：如果需要对k个比特进行枚举，可以使用一个整数从0-2^k-1，然后每个数都可以对应k个数的一种组合，所以我们这里可以从0变换到63.

python代码

python中的数据类型选择：
（1）存储格式选择列表原因：

Python不允许程序员选择采用传值还是传 引用。Python参数传递采用的肯定是“传对象引用”的方式。
Python中的对象有可变对象（number，string，tuple等）和不可变对象之分（list，dict等）。
不可变对象作为函数参数，相当于C语言的值传递（值传递的特点是被调函数对形式参数的任何操作都是作为局部变量进行，不会影响主调函数的实参变量的值。）。
可变对象作为函数参数，相当于C语言的引用传递。（被调函数对形参做的任何操作都影响了主调函数中的实参变量）

所以这里存储选择字符列表。
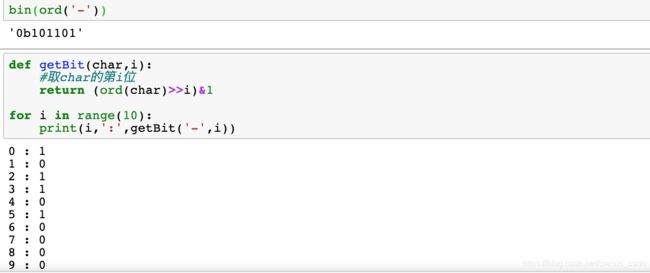
（2）python中字符串不能直接进行位运算，所以需要用到两个命令：ord和chr。
ord用来变成数字形式，chr将数字返回字符串形式。

• ps:这里有个疑问，我还没确认这里为什么还可以输出，python中字符可能不是8bit。待确认。
  
  此外问题： chr出现溢出问题，所以最后还是采用数组形式存储，然后采用位运算。

def turn_off_lights():
    N = int(input())
    for m in range(N):
        #第m个
        #读取原始台灯状态。
        raw_lights =np.zeros((5,6))
        for j in range(5):
            line = input().split(' ')[:6]
            raw_lights[j] = [int(light) for light in line]
        #遍历一遍改变状态
        for first_swich in range(64):
            #构建一个switches记录每一行开关状态。
            switches = np.zeros((5,6))
            bin_s = list(bin(first_swich).lstrip('0b'))
            bin_s = [0]*(6-len(bin_s)) +[int(i) for i in bin_s] #将二进制数转换成定长为6
            #复制一遍
            tmp_lights = deepcopy(raw_lights)
            #一行一行改变状态,从上往下改变，就不要该上面了。
            switch = bin_s
            for j in range(5):
                switches[j] = deepcopy(switch)
                #一行有6个
                for s_index in range(6):
                    if switch[s_index]:#如果按钮是1
                        #改变自己的状态
                        tmp_lights[j][s_index] = int(tmp_lights[j][s_index])^1
                        #按钮左右都要改变状态
                        if s_index>0:
                            tmp_lights[j][s_index-1] = int(tmp_lights[j][s_index-1])^1
                        if s_index<5:
                            tmp_lights[j][s_index+1] =int(tmp_lights[j][s_index+1])^1
                        #按钮下面一行改变状态
                        if j <4 :
                            tmp_lights[j+1][s_index] =int(tmp_lights[j+1][s_index])^ 1
                #下一行的按钮状态就是这一行等的状态，这一行为0即灯关闭，下一行就要为0，这一行为1，下一行就要按灭
                switch = tmp_lights[j]
                #判断最后一行的状态是不是全部关闭，全部关闭则输出
                if j==4 and not tmp_lights[4].any():
                    #输出switches状态
                    print('PUZZLE #%d'%(int(m)))
                    for jj in range(5):
                        print(' '.join([str(int(s)) for s in switches[jj]]))
                    break
turn_off_lights()

结果：

总结：其实枚举是一个比较常用的解法，虽然很朴素，但是很解决很多问题，而且可以根据一些先验知识减少枚举的次数，就可以取到比较好的效果。
此外位运算也是一个在使用中经常被忽视的东西，但是其实位运算很好用，但是在python中使用位运算好像不是很方便，或者是我写法的问题，位运算还是遇到了一些麻烦的，最后还是采用了数据的解法。
明天攻克第二章的内容，然后在做博客分享吧～

---

一些其它的心情分享：
最近肺炎疫情真的很严重，希望一切都快好起来。