伸展树(Splay Tree),也叫分裂树,是一种二叉排序树,它能在O(lgN)内完成插入、查找和删除操作。在伸展树上的一般操作都基于伸展操作:假设想要对一个二叉查找树执行一系列的查找操作,为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法, 在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。伸展树应运而生。其插入、删除、查找操作基本与二叉搜索树的相同。其唯一的不同之处在于每次的插入、删除、查找操作都需要将其对应的节点通过旋转的方式转变为该树的根节点 (ps: 对于插入操作,是插入相应的节点之后,将其转变为根节点。对于删除操作,其实在找到对应的节点,通过旋转将其转变为根节点之后,才进行删除操作)。
类别:二叉排序树
空间效率:O(n)
时间效率:O(log n)内完成插入、查找、删除操作
创造者:Daniel Sleator和Robert Tarjan
优点:每次查询会调整树的结构,使被查询频率高的条目更靠近树根(一般是将每次查询的节点调整为树根节点)。
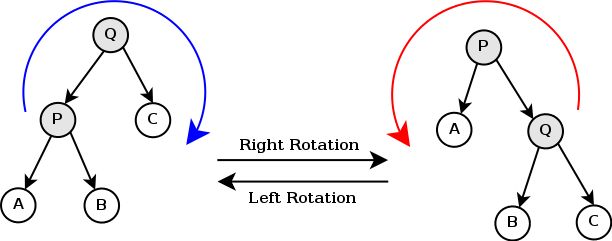
树的旋转是splay的基础,对于二叉查找树来说,树的旋转不破坏查找树的结构。
Splaying
Splaying是Splay Tree中的基本操作,为了让被查询的条目更接近树根,Splay Tree使用了树的旋转操作,同时保证二叉排序树的性质不变。
伸展树的实现方式:
伸展树有两种实现的方式,一种是自顶向下的方式,一种是自底向上的方式。
自底向上的实现方式:
Splaying的操作受以下三种因素影响:
节点x是父节点p的左孩子还是右孩子
节点p是不是根节点
节点p是父节点g的左孩子还是右孩子
自底向上的实现方式定义了三种基本操作:
Zig Step
当p为根节点时,进行zip step操作。
当x是p的左孩子时,对x右旋(以P为顶点);
当x是p的右孩子时,对x左旋(以P为顶点)。
ps:zig操作,可以记忆为一次左旋或者一次右旋操作
Zig-Zig Step
当p不是根节点,且x和p同为左孩子或右孩子时进行Zig-Zig操作。
当x和p同为左孩子时,依次将p(以g为顶点)和x右旋(以P为顶点);
当x和p同为右孩子时,依次将p(以g为顶点)和x左旋(以P为顶点)。
ps:zig-zig操作,可以记忆为两次方向相同的旋转操作
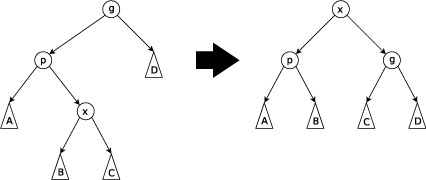
zig-zag step
当p不是根节点,且x和p不同为左孩子或右孩子时,进行Zig-Zag操作。
当p为左孩子,x为右孩子时,将x左旋(以P为顶点)后再右旋(以g为顶点)。
当p为右孩子,x为左孩子时,将x右旋(以P为顶点)后再左旋(以g为顶点)。
ps:zig-zag操作,可以记忆为两次方向不同的旋转操作
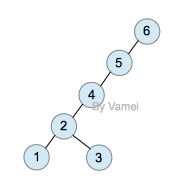
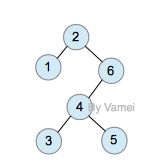
下面我们用一个具体的例子示范。我们将从树中搜索节点2:
上面的第一次查询需要n次操作。然而经过一次查询后,2节点成为了根节点,树的深度大减小。整体上看,树的大部分节点深度都减小。此后对各个节点的查询将更有效率。
自顶向下的实现方式:
普通伸展树的伸展操作需要从根沿树往下的一次遍历,以及而后的从底向上的一次遍历,并在此过程中不断的对树进行相应的旋转操作,使得相应的节点称为根节点。这可以通过保存一些父指针来完成,或者通过将访问路径存储到一个栈中来完成。这两种方法均需要大量的开销,这种方式也被称为自底向上的伸展树实现方式。幸运的是,我们可以采用自顶向下的伸展树的实现方式,这个过程产生的开销可以基本忽略不计。
自顶向下方式的伸展树实现,其原理是将一棵树分割成了三棵,之后再进行相应的合并。
具体操作过程是(假设查找节点X):
先建立两个空子树,一个是LeftTreeMax(简称LTMax),另一个是RightTreeMin(简称RTMin)。其中LTMax子树保存遍历过程中所有小于X的节点,并且LTMax在遍历过程中始终指向该子树中最大的那个节点。不难看出LTMax->Right始终为空。RTMin子树保存遍历过程中所有大于X的节点,RTMin在遍历过程中始终指向该子树中最小的那个节点。同样RTMin->Left也始终为空。因此在合并RTMin和LTMax前,RTMin是所在子树上所有大于X节点中那个最小的并接近X的节点,同理LTMax中所在子树中所有小于X节点中那个最大的并接近X的节点。
从根节点T开始遍历,查找X节点,直到找到或者未找到
如果X节点小于T并且小于T->Left(LL型)则实行一次围绕T的右单旋转,之后T->Left成为新的根节点T',X又小于T',所以从T'劈开的右子树(包括T',也就是从T'的左子树连接处劈开)上的所有节点都大于X,我们将T'挂在RTMin->Left上,并更新RTMin指向T'节点,T'节点是所有大于X节点中最小的那个。
如果X节点小于T,但T->Left为NULL,则未找到X节点,退出循环并将三个子树合并
如果X节点大于T并且大于T->Right(RR型),则实行一次围绕T的左单旋转,这样T->Right成为新的根节点T',X又大于T',所以从T'劈开的左子树(包括T',也就是从T'的右子树连接处劈开)上所有的节点都小于X,我们将T'子树挂在LTMax->Right上,并将LTMax指向新的T'节点,T'节点就是所有小于X节点中最大的那个。
如果X节点大于T,但T-Right为NULL,则未找到X节点,退出循环将三个子树合并
当找到或者未找到X节点退出循环后,合并三个子树。
ps:需要注意的是,对于rl型和lr型其并不进行旋转操作,而直接对其进行劈开,并将其连接到对应的子树节点上。
此时LTMax是所有小于X节点的最大的那个,所以要将中子树(简称为M)的M->Left挂在LTMax->Right上,将M->Right挂在RTMin->Left上。最后更新M为LTMax和RTMin的根节点。
伸展树的节点类代码:
class Node>{
/**
* 对应的键值
*/
T key;
/**
*左孩子节点
*/
Node left;
/**
* 右孩子节点
*/
Node right;
public Node(){
this(null,null,null);
}
public Node(T key){
this(key,null,null);
}
public Node(T key,Node left,Node right){
this.key=key;
this.left=left;
this.right=right;
}
} 核心代码如下:
/**
* @param tree 需要进行伸展操作的树的根节点
* @param key 其需要进行旋转到根节点位子的元素节点的值
* @return 其伸展后树的根节点元素的指针
*/
private Node splay(Node tree,T key){
/*
用于判空排除空指针异常的干扰
*/
if(tree==null||key==null){
return tree;
}
/*
此处采用一个节点node来维护其相应的LeftTreeMax以及RightTreeMin子树部分
其中node.left用于标记RightTreeMin子树
node.right用于标记LeftTreeMax子树
以便于和最后的子树合并操作
*/
Node node =new Node();
//用于标记其左右子树的所有小于key的元素中的最大值以及所有大于key的元素中的最小值
Node leftTreeMax=node;
Node rightTreeMin=node;
while(true){
int cmp=key.compareTo((T) tree.key);
if(cmp<0){
//当不存在需要查找的键的情况下,跳出循环,合并三棵子树
if(tree.left==null){
break;
}
//当其为LL型时,将其进行右旋操作
if(key.compareTo((T)tree.left.key)<0){
tree=rotateRight(tree);
//当树中没有对应的节点时,进行三树合并操作
if(tree.left==null){
break;
}
}
//用于劈开其对应的根节点的左子树,将其拼接到对应的rightTreeMin的左分支上,同时修改对应的中树的节点
rightTreeMin.left=tree;
rightTreeMin=tree;
tree=tree.left;
}
else if(cmp>0){
//当不存在需要查找的键的情况下,跳出循环,合并三棵子树
if(tree.right==null){
break;
}
//当为rr型时,进行左旋操作
if(key.compareTo((T)tree.right.key)>0){
tree=rotateLeft(tree);
if(tree.right==null){
break;
}
}
//用于劈开对应的根节点的右子树,并进行拼接和调整操作
leftTreeMax.right=tree;
leftTreeMax=tree;
tree=tree.right;
}
else{
break;
}
}
//将中树的左子树合并到L树中,将中树的右子树合并到R树中,将中树的左子树合并到L树中
leftTreeMax.right=tree.left;
rightTreeMin.left=tree.right;
//用于合并三棵子树,node.right对应的为L树,node.left对应的为R树
tree.left=node.right;
tree.right=node.left;
return tree;
}
/**
* 用于伸展操作的相应的接口
* @param key
*/
public void splay(T key){
this.root=splay(this.root,key);
}伸展树的具体代码如下:
/**
* @author 学徒
* 该类用于实现伸展树
*/
public class SplayTree >{
//伸展树的根节点
private Node root;
//伸展树的节点的定义
private class Node>{
/**
* 对应的键值
*/
T key;
/**
*左孩子节点
*/
Node left;
/**
* 右孩子节点
*/
Node right;
public Node(){
this(null,null,null);
}
public Node(T key){
this(key,null,null);
}
public Node(T key,Node left,Node right){
this.key=key;
this.left=left;
this.right=right;
}
}
/**
* 对某个节点进行相应的右旋操作
* @param node 需要进行右旋操作的节点本身
* @return 旋转后的子树的根节点
*/
private Node rotateRight(Node node){
Node temp=node.left;
node.left=temp.right;
temp.right=node;
return temp;
}
/**
* 对某个节点进行相应的左旋操作
* @param node 需要进行左旋操作的节点本身
* @return 旋转后的子树的根节点
*/
private Node rotateLeft(Node node){
Node temp=node.right;
node.right=temp.left;
temp.left=node;
return temp;
}
/**
* @param tree 需要进行伸展操作的树的根节点
* @param key 其需要进行旋转到根节点位子的元素节点的值
* @return 其伸展后树的根节点元素的指针
*/
private Node splay(Node tree,T key){
/*
用于判空排除空指针异常的干扰
*/
if(tree==null||key==null){
return tree;
}
/*
此处采用一个节点node来维护其相应的LeftTreeMax以及RightTreeMin子树部分
其中node.left用于标记RightTreeMin子树
node.right用于标记LeftTreeMax子树
以便于和最后的子树合并操作
*/
Node node =new Node();
//用于标记其左右子树的所有小于key的元素中的最大值以及所有大于key的元素中的最小值
Node leftTreeMax=node;
Node rightTreeMin=node;
while(true){
int cmp=key.compareTo((T) tree.key);
if(cmp<0){
//当不存在需要查找的键的情况下,跳出循环,合并三棵子树
if(tree.left==null){
break;
}
//当其为LL型时,将其进行右旋操作
if(key.compareTo((T)tree.left.key)<0){
tree=rotateRight(tree);
//当树中没有对应的节点时,进行三树合并操作
if(tree.left==null){
break;
}
}
//用于劈开其对应的根节点的左子树,将其拼接到对应的rightTreeMin的左分支上,同时修改对应的中树的节点
rightTreeMin.left=tree;
rightTreeMin=tree;
tree=tree.left;
}
else if(cmp>0){
//当不存在需要查找的键的情况下,跳出循环,合并三棵子树
if(tree.right==null){
break;
}
//当为rr型时,进行左旋操作
if(key.compareTo((T)tree.right.key)>0){
tree=rotateLeft(tree);
if(tree.right==null){
break;
}
}
//用于劈开对应的根节点的右子树,并进行拼接和调整操作
leftTreeMax.right=tree;
leftTreeMax=tree;
tree=tree.right;
}
else{
break;
}
}
//将中树的左子树合并到L树中,将中树的右子树合并到R树中,将中树的左子树合并到L树中
leftTreeMax.right=tree.left;
rightTreeMin.left=tree.right;
//用于合并三棵子树,node.right对应的为L树,node.left对应的为R树
tree.left=node.right;
tree.right=node.left;
return tree;
}
/**
* 用于伸展操作的相应的接口
* @param key
*/
public void splay(T key){
this.root=splay(this.root,key);
}
/**
* 用于往树中插入相应的值
* @param value 插入的值
*/
public void insert(T value){
Node node=new Node(value);
if(this.root==null){
this.root=node;
}
else{
//用于进行比较的当前节点
Node temp=this.root;
//当前节点的父节点
Node tem=null;
//当其值不相等的时候
while(temp!=null){
int cmp=temp.key.compareTo(value);
tem=temp;
if(cmp<0){
temp=temp.right;
}
else if(cmp>0){
temp=temp.left;
}
//想插入的节点的值已经存在
else{
break;
}
}
//节点不存在,需要插入相应的节点
if (temp==null){
int cmp=tem.key.compareTo(value);
//往右节点中插入
if(cmp<0){
tem.right=node;
}
else{
tem.left=node;
}
}
//对其进行伸展操作
splay(value);
}
}
/**
* 用于删除相应的节点的操作
* @param key 删除的节点的关键字
*/
public void delete(T key) {
//当存在其对应的键
if (search(key) == null) {
return;
}
//由于search(key)!=null,为此,其根节点为其对应的删除节点
Node node = this.root;
//将其前驱节点转化为根节点
if (this.root.left != null) {
this.root = splay(this.root.left, key);
//移除node节点
this.root.right = node.right;
} else {
this.root = node.right;
}
}
/**
* 用于查找相应的节点的操作
* @param key 查找的节点的关键字
* @return 相应的节点,没找到时,返回null
*/
public Node search(T key){
Node node=this.root;
while(node!=null){
int cmp=node.key.compareTo(key);
if(cmp<0){
node=node.right;
}
else if(cmp>0){
node=node.left;
}
else{
break;
}
}
//当存在相应的节点时,对其进行伸展操作
if(node!=null){
splay(key);
}
return node;
}
/**
* 对其进行前序遍历操作
* @param node 进行遍历的树的根节点
*/
private void preOrder(Node node){
if(node!=null){
System.out.print(node.key+" ");
preOrder(node.left);
preOrder(node.right);
}
}
public void preOrder(){
preOrder(this.root);
}
/**
* 对其进行中序遍历操作
* @param node 进行遍历的树的根节点
*/
private void inOrder(Node node){
if(node!=null){
inOrder(node.left);
System.out.print(node.key+" ");
inOrder(node.right);
}
}
public void inOrder(){
inOrder(this.root);
}
/**
* 获取整个伸展树的最小节点值
* @return 树的最小节点的值
*/
public T getMin(){
Node node=this.root;
while(node.left!=null){
node=node.left;
}
if(node!=null){
return (T)node.key;
}
else{
return null;
}
}
/**
* 获取整个伸展树的最大节点值
* @return 树的最大节点的值
*/
public T getMax(){
Node node=this.root;
while(node.right!=null){
node=node.right;
}
if(node!=null){
return (T)node.key;
}
else{
return null;
}
}
/**
* 打印"伸展树"
*
* key -- 节点的键值
* direction -- 0,表示该节点是根节点;
* -1,表示该节点是它的父结点的左孩子;
* 1,表示该节点是它的父结点的右孩子。
*/
private void print(Node tree, T key, int direction) {
if(tree != null) {
// tree是根节点
if(direction==0) {
System.out.printf("%2d is root\n", tree.key);
}
// tree是分支节点
else {
System.out.printf("%2d is %2d's %6s child\n", tree.key, key, direction == 1 ? "right" : "left");
}
print(tree.left, tree.key, -1);
print(tree.right,tree.key, 1);
}
}
public void print() {
if (root != null) {
print(root, root.key, 0);
}
}
}
测试伸展树的代码如下:
/**
* @author 学徒
* 伸展树的测试程序
*/
public class SplayTreeTest {
private static final int arr[] = {10,50,40,30,20,60};
public static void main(String[] args) {
int i, ilen;
SplayTree tree=new SplayTree();
System.out.print("== 依次添加: ");
ilen = arr.length;
for(i=0; i 注意点:
伸展树并没有AVL的平衡要求,任意节点的左右子树可以相差任意深度。与二叉搜索树类似,伸展树的单次搜索也可能需要n次操作。但伸展树可以保证,m次的连续搜索操作的复杂度为mlog(n)的量级,而不是mn量级。
应用
Splay Tree可以方便的解决一些区间问题,根据不同形状二叉树中序遍历结果不变的特性,可以将区间按顺序建二叉查找树。每次自下而上的一套splay都可以将x移动到根节点的位置,利用这个特性,可以方便的利用Lazy的思想进行区间操作。对于每个节点记录size,代表子树中节点的数目,这样就可以很方便地查找区间中的第k小或第k大元素。对于一段要处理的区间[x, y],首先splay x-1到root,再splay y+1到root的右孩子,这时root的右孩子的左孩子对应子树就是整个区间。这样,大部分区间问题都可以很方便的解决,操作同样也适用于一个或多个条目的添加或删除,和区间的移动。
用于热点数据的存放,比如网络应用中,某些固定内容会被大量重复访问。伸展树可以让这种重复搜索以很高的效率完成。
参考自:Splay Tree和纸上谈兵: 伸展树 (splay tree)以及数据结构与算法分析之伸展树(splaytree)