秋末的落叶 题解
传送门:https://www.luogu.com.cn/problem/U121886
Part 1:疏通题意
首先,我们从题意和样例解释中很容易提取到以下信息:
\(1、\)本题是一个图论题,\(maple[i]\)是第\(i\)个节点的点权,违和感则可以抽象成无向边的边权
\(2、\)如果一条边连接的两个端点都在所选中的子图中,那么这条边也必须在子图中
\(3、\)题目所求:找到一个连通子图使得点权和除以边权和最大(在以下数学证明中,我们用\(t\)表示这个值)
Part 2:数学证明
首先已经告诉大家这是一个贪心题那就大大降低了这个题的难度
我们的任务简化为:找到一个贪心的办法(好像没啥实质性变化)
首先考虑图的两种基本形态:环状和链状
我们看看,环状的子图和链状的子图中,可不可以证明其中一种一定比另一种更优,这样我们的检索范围就会大大减小
灵魂画师请见谅
开始证明:
那么在这个简单环中,我们设置以下四个变量来表示环和链的\(t\)值
用\(t_{abc}\)来表示环的\(t\)值,有\(t_{abc}=\frac{a+b+c}{x+y+z}\)
用\(t_{ab}\)表示两节点链\(ab\)的\(t\)值,有\(t_{ab}=\frac{a+b}{x}\)
用\(t_{bc}\)表示两节点链\(bc\)的\(t\)值,有\(t_{bc}=\frac{b+c}{y}\)
用\(t_{ac}\)表示两节点链链\(ac\)的\(t\)值,有\(t_{ac}=\frac{a+c}{z}\)
首先,不妨设\(t_{ab}\geq t_{bc}\geq t_{ac}\),(PS:如果不满足,交换顺序即可,不影响证明的正确性)
那么化简\(t_{ab},t_{bc},t_{ac}\)得到了一个包含三个不等式的不等式组:
\( \begin{cases} ay+by\geq bx+cx\\ bz+cz\geq ay+cy\\ az+bz\geq ax+cx\\ \end{cases} \)
因为 \(t_{ab}\geq t_{bc}\geq t_{ac}\),只需要证明\(t_{ab}>t_{abc}\),即可说明每一个环本身中,至少存在一个两节点链比这个环更优
左式:\(t_{ab}=\frac{a+b}{x}\),右式:\(t_{abc}=\frac{a+b+c}{x+y+z}\)
\(1、\)同时乘以:\(x(x+y+z)\) 左式:\((a+b)(x+y+z)\),右式:\(x(a+b+c)\)
\(2、\)同时减去:\(x(a+b)\) 左式:\((y+z)(a+b)\),右式:\(cx\)
\(3、\)化简一步:左式:\(ay+by+az+bz\),右式:\(cx\)
\(4、\)根据上面推出的不等式组:\(ay+by+az+bz\geq bx+cx+ax+cx=2cx+ax+bx\)
\(5、\)又因为:\(a、b、c、x、y、z\)均为正数,所以:\(2cx+ax+bx>cx\)
\(6、\)推出:左式\(>\)右式,即\(t_{ab}>t_{abc}\)
综上所述:每一个环本身中,至少存在一个两节点链比这个环更优
证毕
那么得到了这样一个结果——每一个环本身中,至少存在一个两节点链比这个环更优。现在,我们就不用考虑环的情况了
既然我们可以证明环和链之间的大小关系,进一步思考:链和链之间的大小关系可不可以证明呢?
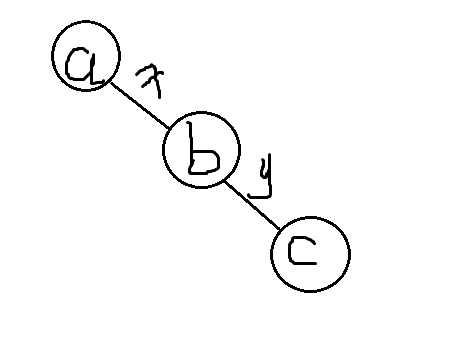
让我们从最短的链证起,请看图:
开始证明:
在这个三个节点组成的链中,我们设置以下三个变量来表示两个短链和一个长链的\(t\)值
用\(t_{abc}\)表示长链的\(t\)值,有\(t_{abc}=\frac{a+b+c}{x+y}\)
用\(t_{ab}\)表示短链\(ab\)的\(t\)值,有\(t_{ab}=\frac{a+b}{x}\)
用\(t_{bc}\)表示短链\(bc\)的\(t\)值,有\(t_{bc}=\frac{b+c}{y}\)
首先,不妨设:\(t_{ab}\geq t_{bc}\)(PS:如果不满足,依旧交换即可,不影响证明的正确性)
那么化简这个式子,得到一个不等式:\(ay+by\geq bx+cx\)
因为:\(t_{ab}\geq t_{bc}\),只需证\(t_{ab}>t_{abc}\),即可说明在任意一三节点个长链本身中,至少存在一个两节点短链比这个长链更优
左式:\(t_{ab}=\frac{a+b}{x}\),右式:\(t_{abc}=\frac{a+b+c}{x+y}\)
\(1、\)同时乘以:\(x(x+y)\) 左式:\((a+b)(x+y)\),右式:\(x(a+b+c)\)
\(2、\)同时减去:\(x(a+b)\) 左式:\(y(a+b)\),右式:\(cx\)
\(3、\)化简一步:左式:\(ay+by\),右式:\(cx\)
\(4、\)根据上面推出的不等式:\(ay+by\geq bx+cx\),且\(x、y、a、b、c\)均为正数,有\(bx>0\),所以推出\(ay+by>cx\)
\(5、\)推出:左式\(>\)右式,即\(t_{ab}>t_{abc}\)
综上所述:在任意一三节点个长链本身中,至少存在一个两节点短链比这个长链更优
(PS:感谢XMZ帮助我整理证明过程Orz)
但是还没有完,我们还需要得知长度为\(n\)的链和长度为\(2\)的链谁更优一些
\(n\)个节点链可以看成是\(n-1\)节点链和\(n\)节点链进行比较,而\(n-1\)又可以看成\(n-2\)节点链和\(n-1\)节点链比较
像上面这样一直进行递推下去,问题就又转化成了:三节点链和两节点链哪个更优这个问题,所以上面的证明方法对于无限长的链也都适用
根据沃兹基·施沃德(我自己说的)法则(应该是数学归纳法)可以把上面的证明推广到下面这个形式:
对于任意长度链,都在它本身中至少存在一个两节点链比它更优
证毕
Part 3:贪心思路
有了上面那么冗长的证明,我们终于归纳出了一个简单的结果:
答案一定是一个两节点构成的链
所以我们的贪心思路就是:找到一个\(t\)值最大的两节点链\(ab\)
妙啊!——zay
所以我们需要一个\(val\)数组,存放点权,每次输入三元组的时候,计算这个两节点链的\(t\)值,维护一个\(maxn\)最大即可
Part 4:代码实现
这个小学生都会吧……(所以这题是红题)
#include
using namespace std;
double maxn,value[505];
int n,m;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%lf",&value[i]);
for(int i=1,a,b;i<=m;i++){
double c;
scanf("%d%d%lf",&a,&b,&c);
double k=(value[a]+value[b])/c;
if(k>maxn) maxn=k;
}
printf("%.3lf\n",maxn);
return 0;
}