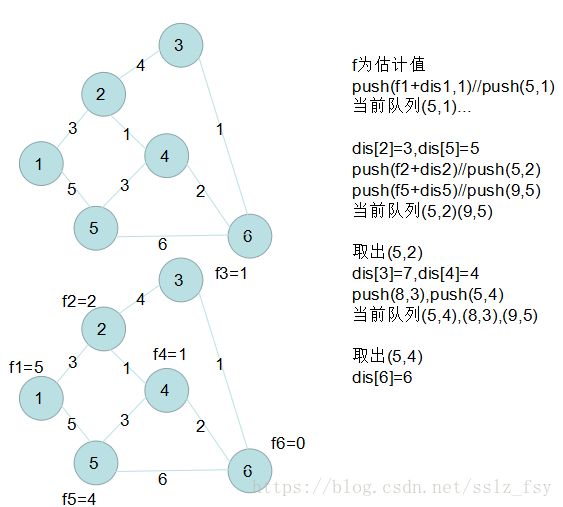
A*(第k短路)
如果给定一个“目标状态”,需要求出从初态到目标状态的最小代价,那么优先队列BFS的这个“优先策略”显然是不完善的。一个状态的当前代价最小,只能说明从起始状态到该状态的代价很小,而在未来的搜索中,从该状态到目标状态可能会花费很大的代价:另外一些状态虽然当前代价略大,但是未来到目标状态的代价可能会很小,于是从起始状态到目标状态的总代价反而更优。优先队列BFS会优先选择前者的分支.
为了提高搜索效率,我们很自然地想到,可以对未来可能产生的代价进行预估。详细地讲,我们设计一个“估价函数”,以任意“状态”为输入,计算出从该状态到目标状态所需代价的估计值。在搜索中,我们仍然维护一一个堆,不断从堆中取出“当前代价+未来估价”最小的状态进行扩展。
为了保证第-次从堆中取出目标状态时得到的就是最优解,我们设计的估价函数需要满足一个基本准则: 设当前状态state到目标状态所需代价的估计值为f(state)。 设在未来的搜索中,实际求出的从当前状态state 到目标状态的最小代价为g(state)。 对于任意的state,应该有f(state) ≤g(state)。
也就是说,估价函数的估值不能大于未来实际代价,估价比实际代价更优。
很快就搜完了
于是乎,算出恰当的f很关键,f要尽量大但小于最优解
第K短路
第几次出队就是第几短,于是终点出了k次就是第k短路了
按照dijsktra的思想,我们每次取出dis[x]+f[x]最小的
然后更新所有能到达的点
发现f[x]可以取到终点的dis,这样尽量大且一定比现在的解小
于是先倒着spfa一遍(搞出f)
然后A*,直到终点第k次走到
#include
#define N 1005
#define M 100005
using namespace std;
int first[N],next[M*2],to[M*2],w[M*2],tot;
int first2[N],next2[M*2],to2[M*2],w2[M*2],tot2;
int dis[N],vis[N],n,m,s,t,k;
struct Node{
int pos,f,dis;
bool operator < (Node a) const{
return a.f+a.dis q;
int read(){
int cnt=0;char ch=0;
while(!isdigit(ch))ch=getchar();
while(isdigit(ch))cnt=cnt*10+(ch-'0'),ch=getchar();
return cnt;
}
void add(int x,int y,int z){
next[++tot]=first[x],first[x]=tot,to[tot]=y,w[tot]=z;
next2[++tot2]=first2[y],first2[y]=tot2,to2[tot2]=x,w2[tot2]=z;
}
void spfa(){
queue q1;
q1.push(t);
memset(dis,0x3fffffff,sizeof(dis));
dis[t]=0;
while(!q1.empty()){
int x=q1.front();
q1.pop(),vis[x]=0;
for(int i=first2[x];i;i=next2[i]){
int T=to2[i];
if(dis[T]>dis[x]+w2[i]){
dis[T]=dis[x]+w2[i];
if(!vis[T]) q1.push(T),vis[T]=1;
}
}
}
}
int astar(){
if(dis[s]==0x3fffffff) return -1;
int times[N];
memset(times,0,sizeof(times));
Node tmp,h;
h.pos=s,h.f=0,h.dis=0;
q.push(h);
while(!q.empty()){
Node x=q.top(); q.pop();
times[x.pos]++;
if(times[x.pos]==k&&x.pos==t) return x.dis;
if(times[x.pos]>k) continue;
for(int i=first[x.pos];i;i=next[i]){
tmp.dis=x.dis+w[i];
tmp.f=dis[to[i]];
tmp.pos=to[i];
q.push(tmp);
}
}
return -1;
}
int main(){
n=read(),m=read();
for(int i=1;i<=m;i++){
int x=read(),y=read(),z=read();
add(x,y,z);
}
s=read(),t=read(),k=read();
if(s==t) k++;
spfa();
cout<