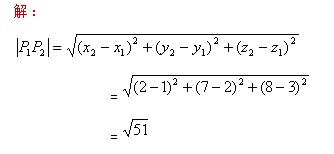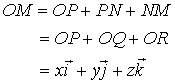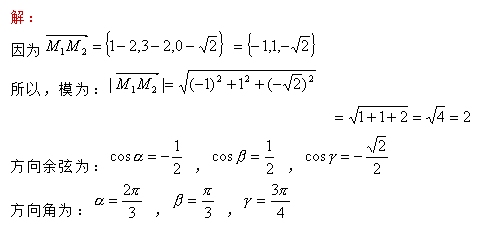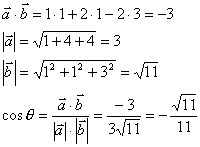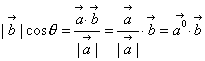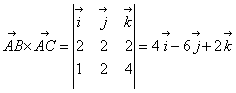http://kjwy.5any.com/gdsx22/other/kcjg/index.htm
第七章 向量代数与空间解析几何
§7.1 空间直角坐标系
7.1.1 空间点的直角坐标系
过空间一个定点O,作三条互相垂直、具有相同的长度单位的数轴它们分别称为x轴、y轴和z轴,并使得它们的正向符合右手法则,即以右手握住z轴,当右手的四个手指从正向x轴,以![]() 角度转向正向y轴时,大拇指的指向就是z轴的正向,如图7-1。
角度转向正向y轴时,大拇指的指向就是z轴的正向,如图7-1。
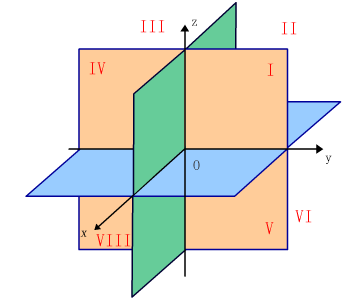
图中箭头的指向表示x轴、y轴、z轴的正向。这样的三条坐标轴就组成了一个空间直角坐标系。点O叫做坐标原点(或原点)。
三条坐标轴中的任意两条可以确定一个平面,这样定出的三个平面统称为坐标面。由x轴及y轴所确定的坐标面叫做xOy面,另两个由y轴及z轴和由z轴及x轴所确定的坐标面,分别叫做yOz面及zOx面。
三个坐标面把空间分成八个部分,每一部分叫做卦限。含有x轴、y轴与z轴正半轴的那个卦限叫做第一个卦限,其它第二、第三、第四卦限,在xOy面的上方,按逆时针方向确定。第五至第八卦限,在xOy面的下方,由第一卦限之下的第五卦限,按逆时针方向确定,这八个卦限分别用字母I、II、III、IV、V、VI、VII、VIII表示。
7.1.2 点的坐标
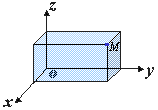
设M为空间一已知点。我们过点M作三个平面分别垂直于x轴、y轴和z轴,它们与x轴、y轴、z轴的交点依次为P、Q、R(图7-2),这三点在x轴、y轴、z轴上的坐标依次为x、y、z。于是空间的一点M就唯一地确定了一个有序数组x,y,z;反过来,已知一有序数组x,y,z,我们可以在x轴上取坐标为x的点P,在y轴上取坐标为y的点Q,在z轴上取坐标为z的点R,然后通过P、Q与R分别作x轴、y轴和z轴的垂直平面。这三个垂直平面的交点M便是由有序数组x,y,z所确定的唯一的点。这样,就建立了空间的点M和有序数组x,y,z之间的一一对应关系。这组数x,y,z就叫做点M的坐标,并依次称x,y和z为点M的横坐标,纵坐标和竖坐标。坐标为x,y,z的点M通常记为M(x,y,z)。
在坐标面上与坐标轴上的点有其特性,具体的说:
- 如果点M在yOz面上,则在点M的坐标中x=0;点M在zOx面上,则在点M的坐标中y=0;点M在xOy面上,则在点M的坐标中z=0。即在坐标面上的点的坐标特点是:点在哪根坐标面上,点的哪个坐标为零。如xoy面的方程为
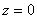 ,则xoy面上的点是
,则xoy面上的点是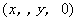 。
。 - 如果点M在x轴上,则在点M的坐标中y=z=0;点M在y轴上,则在点M的坐标中z=x=0;点M在z轴上,则在点M的坐标中x=y=0。即在坐标轴上的点的坐标特点是:点在哪根坐标轴上,则哪个坐标非零,而点的另外两个坐标为零。
- 如果点M为原点,则x=y=z=0。
7.1.3 空间两点间的距离
设![]() 、
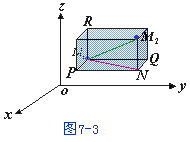
、![]() 为空间两点,为了用两点的坐标来表达它们之间的距离d,我们过M1、M2各作三个分别垂直于三条坐标轴的平面。这六个平面围成一个以M1M2为对角线的长方体(图7-3)。
为空间两点,为了用两点的坐标来表达它们之间的距离d,我们过M1、M2各作三个分别垂直于三条坐标轴的平面。这六个平面围成一个以M1M2为对角线的长方体(图7-3)。
由于![]() 为直角,
为直角,![]() 为直角三角形,所以
为直角三角形,所以
![]()
![]()
又 ![]() 也是直角三角形,且
也是直角三角形,且![]() ,所以
,所以
![]()
由于![]() ,
, ![]() ,
, ![]() ,
,
所以
![]()
这就是空间两点间的距离公式。特殊地,点![]() 与坐标原点
与坐标原点![]() 的距离为
的距离为
![]()
例1:求两点![]() 与
与![]() 的距离。
的距离。
例2:求证以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是一个等腰三角形。
三点为顶点的三角形是一个等腰三角形。
分析:要证明一个三角形是等腰三角形,只要证明在该三角形中有两条边相等方可,由于给出了三个点的坐标,因此用两点间的距离公式解决。
例3:设P在x轴上,它到![]() 的距离为到点
的距离为到点![]() 的距离的两倍,求点P的坐标。
的距离的两倍,求点P的坐标。
分析:由假设有:![]() 2
2![]()
注意到点P在X轴上,由在坐标轴上的点的特点,
可设点P的坐标为(x,0,0)。
利用两点间距离公式方可求出点P的坐标。
思考题
1、写出点P(a,b,c)关于坐标面、坐标轴、原点的对称点的坐标。
2、过点![]() 分别作平行于z轴的直线和平行于xOy面的平面,问在它们上面的点的坐标各有什么特点?
分别作平行于z轴的直线和平行于xOy面的平面,问在它们上面的点的坐标各有什么特点?
§7.2 向量及其线性运算
7.2.1 向量概念
1、向量的定义
定义 既有大小,又有方向的量叫做向量(Vector)。
2、向量的几何表示
在几何上,向量用有向线段来表示,有向线段长度表示向量的大小,有向线段的方向表示向量的方向。其实有向线段本身也是向量,称为几何向量。今后我们将以它为代表来研究向量。从而以M1为起点、M2为终点的有向线段所表示的向量,记作![]() (图7-4)。
(图7-4)。
有时也用一个粗体字母或书写体用一个上面加箭头的字母来表示向量。例如a、i、v、F或![]() 、
、![]() 、
、![]() 、
、![]() 等等。
等等。
以坐标原点O为起点,向一个点M引向量![]() ,这个向量叫做点M对于点O的向径,常用粗体字r表示。
,这个向量叫做点M对于点O的向径,常用粗体字r表示。
3、向量的模
向量大小长(即几何向量的长度)称为向量的模;如向量![]() 、
、![]() 、
、![]() 的模依次记作
的模依次记作![]() 、
、![]() 、
、![]() 。
。
模为1的向量称为单位向量;
模为零的向量称为零向量;因为零向量的模为零,所以表示零向量的几何长度为零,从而起点与终点重合,方向不定(注意:零向量不是没有方向,而是方向可以任意)。
4、向量的相等
在实际问题中,有些向量与其起点有关,有些向量与其起点无关。由于一切向量的共性是它们都有大小和方向,所以在数学上我们只研究与起点无关的向量,并称这种向量为自由向量(以后简称向量),即只考虑向量的大小和方向,而不论它的起点在什么地方。
在只讨论自由向量的约定下,向量可以平行移动,所以两个向量相等的定义如下:
定义 如果两个向量![]() 和
和![]() 的大小相等,且方向相同,我们就说向量
的大小相等,且方向相同,我们就说向量![]() 和
和![]() 是相等的,记作
是相等的,记作![]() 。
。
即:经过平行移动后能完全重合的向量是相等向量,或者说它们是同一个向量。
向量的模能否为负数? 两个非零向量如果它们的方向相同或者相反,就称这两个向量平行。向量![]() 和
和![]() 平行,记作
平行,记作![]() 。由于零向量的方向可以看作是任意的,因此可以认为零向量与任何向量都平行。
。由于零向量的方向可以看作是任意的,因此可以认为零向量与任何向量都平行。
7.2.2 向量的线性运算
1. 向量的加法运算规律
设有两个向量![]() 与
与![]() ,任取一点A,作
,任取一点A,作![]() ,再以B为起点,作
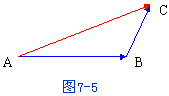
,再以B为起点,作![]() ,连接AC(图7-5),那末向量
,连接AC(图7-5),那末向量![]() 称为向量
称为向量![]() 与
与![]() 的和,记作
的和,记作![]() ,即
,即 ![]()
上述作出两向量之和的方法叫做向量相加的三角形法则。
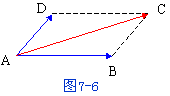
力学上有求合力的平行四边形法则,仿此,我们也有向量加法的平行四边形法则。这就是:当向量![]() 与
与![]() 不平行时,作
不平行时,作![]() ,
,![]() ,以
,以![]() 、
、![]() 为边作一平行四边形ABCD,连接对角线AC(图7-6),显然向量
为边作一平行四边形ABCD,连接对角线AC(图7-6),显然向量![]() 即等于向量
即等于向量![]() 与
与![]() 的和
的和![]() 。
。
向量的加法符合下列运算规律:
(1)交换律:![]() ;
;
(2)结合律:![]()
由两向量求和的三角形法则,可知向量的模满足三角形不等式:![]()
这是因为三角形两边之和大于第三边,其中等号当且仅当![]() 与
与![]() 同向时成立。
同向时成立。
2.数乘以向量
定义 向量![]() 与实数
与实数![]() 的乘积
的乘积![]() ,是指满足下列条件的一个向量:它的模
,是指满足下列条件的一个向量:它的模 ![]() ,
,
它的方向:
- 当
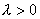 时与
时与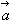 相同;
相同; - 当
 时与
时与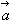 相反;
相反; - 当
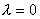 时,
时,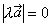 ,即
,即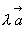 为零向量,这时它的方向可以是任意的。
为零向量,这时它的方向可以是任意的。
因此 向量![]() 与
与![]() 是平行向量,即
是平行向量,即 ![]() 。特别有,
。特别有,![]()
向量与数的乘积符合下列运算规律:
(1)结合律:![]() ;
;
(2)分配律:![]()
![]()
我们称平行于同一直线的向量为共线向量。
由于向量![]() 与
与![]() 平行,因此我们常用向量与数的乘积来说明两个向量的平行关系。即有:
平行,因此我们常用向量与数的乘积来说明两个向量的平行关系。即有:
定理1 设向量![]() ,那末,向量
,那末,向量![]() 平行于
平行于![]() 的充分必要条件是:存在唯一的实数
的充分必要条件是:存在唯一的实数![]() ,使
,使![]() 。
。
先证必要性(![]() )即要从条件
)即要从条件![]() 平行于
平行于![]()
![]() 两向量相等:
两向量相等:![]() 。
。
分析:要证明两向量相等,即证明:(1)向量![]() 、
、![]() 方向相同;(2)模相等。
方向相同;(2)模相等。
证明:(1)先证必要性(![]() )
)
首先证明![]() 、
、![]() 方向相同:
方向相同:
若向量![]() 与
与![]() 反向,取
反向,取![]() ,
,
从而![]() 与
与![]() 恒同向;
恒同向;
其次证明![]() 、
、![]() 模相等:
模相等:
因为![]()
所以![]() 、
、![]() 同向且等模,从而两向量相等,即
同向且等模,从而两向量相等,即![]() 。
。
(2)再证充分性![]()
因为![]() ,
,
由数乘以向量的定义知,![]() 平行于
平行于![]() 。 证毕。
。 证毕。
有了数乘以向量的运算后,我们可以证明:任何一个非零向量![]() 都可以由它的模
都可以由它的模![]() 乘一个与它同方向的单位向量
乘一个与它同方向的单位向量![]() 来表示,即
来表示,即![]() =
=![]() 。
。
事实上:设![]() 表示与非零向量
表示与非零向量![]() 同方向的单位向量,由向量与数的乘积的定义,由于
同方向的单位向量,由向量与数的乘积的定义,由于![]() ,所以
,所以![]() 与
与![]() 的方向相同,即
的方向相同,即![]() 与
与![]() 的方向相同。又因
的方向相同。又因![]() 的模是
的模是 ![]() ,即
,即![]() 与
与![]() 的模也相同,因此,
的模也相同,因此, ![]() =
=![]() (*).
(*).
我们规定,当![]() 时,
时,![]() 。由此,(*)式又可写成
。由此,(*)式又可写成![]()
这表示一个非零向量除以它的模其结果是一个与原向量同方向的单位向量。
3. 负向量、向量的减法
我们用![]() 表示
表示![]() ,称为向量
,称为向量![]() 的负向量。
的负向量。
不难验证:![]() 与
与![]() 的模相等,方向相反;且
的模相等,方向相反;且![]() 。
。
由此,我们定义两个向量![]() 与
与![]() 的差:
的差:
定义 向量![]() 与向量
与向量![]() 的负向量
的负向量![]() 的和,称为向量
的和,称为向量![]() 与
与![]() 的差,记为
的差,记为![]() ,即有
,即有 ![]()
由定义可知,![]() =0
=0
若记 ![]() ,则有
,则有 ![]()
这说明向量的减法实质上是向量加法的逆运算。
例4:设![]() =
=![]() +5
+5![]() ,
,![]() =-6
=-6![]() +18
+18![]() ,
,![]() =8(
=8(![]() -
-![]() ),求证:A、B、D三点共线。
),求证:A、B、D三点共线。
分析:
要证明ABD三点共线即要证明向量![]() 与
与![]() 平行。要证明两个向量平行,即证明它们同向或反向。证明两个向量同向或反向,即证明它们之间成倍数关系,即
平行。要证明两个向量平行,即证明它们同向或反向。证明两个向量同向或反向,即证明它们之间成倍数关系,即![]() =
=![]()
![]() 。
。
证明:
![]() =
=![]() +
+![]() =(-6
=(-6![]() +18
+18![]() )+8(
)+8(![]() -
-![]() )=2
)=2![]() +10
+10![]() =2(
=2(![]() +5
+5![]() )=2
)=2![]()
![]() ,
,![]() 同向(2>0),A,B,D三点共线。
同向(2>0),A,B,D三点共线。
例5:试用向量方法证明:对角线互相平分的四边形必是平行四边形。
分析:要证明一个四边形是平行四边形可以证明一组对边既平行又相等。
等价于证明![]() =
=![]()
注意到![]() =
=![]() =
=![]()
![]()
![]() =
=![]() =
=![]()
![]()
而 ![]() =
=![]() +
+![]()
![]() =
=![]() +
+![]() =
=![]() +
+![]()
所以 ![]() =
=![]()
证明:
![]()
![]() =
=![]()
![]() =
=![]()
∴![]() =
=![]() +
+![]() =
=![]() +
+![]() =
=![]()
![]() 与
与![]() 平行且相等。
平行且相等。
所以,对角线互相平分的四边形是平行四边形。
§7.3 向量的坐标表示式
7.3.1 向量的坐标表示式
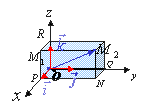
在空间建立一个直角坐标系,沿x轴,y轴,z轴的正方向各取单位向量依次记为![]() 称为空间直角坐标系的三个基本单位向量。
称为空间直角坐标系的三个基本单位向量。
对于任何非零向量 ![]() ,恒可作向经
,恒可作向经![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作三个平面分别垂直于x轴,y轴,z轴。依次得交点
作三个平面分别垂直于x轴,y轴,z轴。依次得交点![]() ,
,![]() ,
,![]() 。由图(图7-7)可知:
。由图(图7-7)可知:
即![]()
该式称为向量的坐标表示式,有时也记为![]() 或
或![]() ,其中x,y,z也称为向量
,其中x,y,z也称为向量![]() 的坐标。
的坐标。
7.3.2 向量线性运算的坐标表示
设![]() ,
,![]() 或
或![]() ,
,![]()
利用向量加法的交换律与结合律,以及向量与数乘法的结合律与分配律,有
![]()
![]()
![]() 为数)
为数)
即![]()
![]()
由此可见,对向量进行加、减及与数相乘,只须对向量的各个坐标分别进行相应的数量运算就行了。
在7.2.2的定理1指出,当向量![]() 时,和量
时,和量![]() 相当于
相当于![]() ,按坐标表示式即为
,按坐标表示式即为 ![]()
特别地,如果![]() 则
则![]()
有![]() 即两向量相等对应坐标等。
即两向量相等对应坐标等。
例6:设![]() 和
和![]() 为两已知点,求向量
为两已知点,求向量![]() 的坐标表示式。
的坐标表示式。
解:
作向径![]() (如图),则有
(如图),则有
![]()
![]()
例7:设![]() 和
和![]() 为两已知点,而在AB直线上的点M分有向线段
为两已知点,而在AB直线上的点M分有向线段![]() 为两个有向线段
为两个有向线段![]() 与
与![]() ,使它们的值的比等于某数
,使它们的值的比等于某数![]() ,即
,即![]() ,求分点M的坐标x、y及z。
,求分点M的坐标x、y及z。
解:
设点![]() 的坐标为
的坐标为![]() ,因为
,因为![]() 与
与![]() 在一直线上如上图,所以依题意有
在一直线上如上图,所以依题意有![]()
![]() ,则
,则![]()
![]()
由两向量相等对应坐标等,有 ![]()
![]()
![]()
点M叫做有向线段![]() 的定比分点。当
的定比分点。当![]() 时,点M是有向线段
时,点M是有向线段![]() 的中点,其坐标为
的中点,其坐标为 ![]() ,
, ![]() ,
, ![]()
例8:设![]() 、
、![]() ,求:
,求:![]() ,
,![]() ,
,![]() ,
,![]()
解:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
7.3.3 向量的模与方向余弦的坐标表示式
向量可以用它的模和方向来表示,也可以用它的坐标来表示。为了应用上的方便,有必要找出这两种表示法之间的联系,就是说要找出向量的坐标与向量的模、方向之间的联系。
对于非零向量![]() ,由向量的定义可知:它的模为
,由向量的定义可知:它的模为![]() 。它的方向,可以用它与三条坐标轴的夹角
。它的方向,可以用它与三条坐标轴的夹角![]() 、
、![]() 、
、![]()
![]() 、
、![]() 、
、![]() )来表示,并称
)来表示,并称![]() 、
、![]() 、
、![]() 为非零向量
为非零向量![]() 的方向角,而
的方向角,而![]() 就称为该向量的方向余弦。由图(图7-8)可知:
就称为该向量的方向余弦。由图(图7-8)可知:
其中![]()
上述讨论表明:当已知非零向量![]() 的坐标
的坐标![]() 表示后,可按下列公式计算它的模与方向余弦:
表示后,可按下列公式计算它的模与方向余弦:![]() 、
、
同时,若以知向量![]() 的模与方向余弦,也可以按下列公式计算其坐标:
的模与方向余弦,也可以按下列公式计算其坐标:
![]()
把方向余弦公式的三个等式两边分别平方后相加,便得到
这就是说,任一向量的方向余弦的平方和等于1。
由上面讨论知,与非零向量![]() 同方向的单位向量为
同方向的单位向量为
例9:求平行于向量![]() 的单位向量的分解式。
的单位向量的分解式。
例10:设![]() ,求向量
,求向量![]() ,
,![]() ,
,![]() 的方向余弦。
的方向余弦。
![]()
例11:设有向量![]() 已知
已知![]() ,它与x轴和y轴的夹角分别为
,它与x轴和y轴的夹角分别为![]() 和
和![]() ,如果P1的坐标为(1,0,3),求P2的坐标。
,如果P1的坐标为(1,0,3),求P2的坐标。
例12:设![]() ;
;![]() ;
;![]() ,求向量
,求向量![]() 在x轴上的投影及在y轴上的分向量。
在x轴上的投影及在y轴上的分向量。
例16:设已知两点![]() 和
和![]() ,计算向量
,计算向量![]() 的模、方向余弦和方向角。
的模、方向余弦和方向角。
例17:设已知两点![]() 和
和![]() ,求方向和
,求方向和![]() 一致的单位向量。
一致的单位向量。
7.4.1 两向量的数量积
1.定义
由力学知,一物体在常力![]() 作用下沿直线从点M1移动到点M2,以
作用下沿直线从点M1移动到点M2,以![]() 表示位移
表示位移![]() ,则力
,则力![]() 作所的功为
作所的功为 ![]() ,其中
,其中![]() 为
为![]() 与
与![]() 的夹角。
的夹角。
由此抽象出两个向量的数量积的定义:
定义 设![]() 是两个向量,称
是两个向量,称![]() 、
、![]() 及它们的夹角
及它们的夹角![]() 的余弦的乘积为向量
的余弦的乘积为向量![]() 的数量积,记作
的数量积,记作![]() ,即
,即
![]()
其中![]() 为两向量
为两向量![]() 的夹角,是指将向量
的夹角,是指将向量![]() 平移到相同起点后,它们之间的不大于180°的夹角,由定义可知,两个向量的数量积其结果是一个数。
平移到相同起点后,它们之间的不大于180°的夹角,由定义可知,两个向量的数量积其结果是一个数。
根据这个定义,上述问题中力所作的功W是力![]() 与位移
与位移![]() 的数量积,即
的数量积,即
![]()
由数量积的定义可以推得:
(1)![]()
这是因为夹角![]() ,所以
,所以![]() 。
。
(2)两个向量![]() 垂直的充分必要条件是它们的数量积为零。
垂直的充分必要条件是它们的数量积为零。
即![]()
![]()
![]() 。
。
事实上:“![]() ”如果
”如果![]() ,由于,
,由于,![]() ,
,![]() ,所以
,所以![]() ,
,
![]()
![]() ,即
,即![]()
由于零向量的方向可以看作是任意的,故可以认为零向量与任何向量都垂直。
由数量积的定义还可以知道:
![]()
![]()
![]()
2.数量积的运算规律
(1)交换律:![]()
而![]() ,且
,且![]()
所以![]()
(2)分配律:![]() ,
,
(3)结合律:![]() ,
,![]() 为常数。
为常数。
3.数量积的坐标表示式
设![]() ,
,![]() 。按数量积的运算规律可得
。按数量积的运算规律可得
![]()
![]()
![]()
![]()
![]()
![]()
![]()
注意到:![]() ,
,
![]()
![]()
因而得
![]()
这就是两个向量的数量积的坐标表示式。
由于![]() ,所以当
,所以当![]() 都不是零向量时,有
都不是零向量时,有
以数量积的坐标表示式及向量的模的坐标表示式代入上式,就得
![]()
这就是两向量夹角余弦的坐标表示式。
4.举例
例18:设![]() ,求两向量夹角的余弦。
,求两向量夹角的余弦。
解:
例19:证明![]() 与向量[(
与向量[(![]() )
)![]() -(
-(![]() )
)![]() ]垂直
]垂直
分析:证明两向量是垂直,等价于证明数量积为零。
证:![]()
![]() -
-![]()
=![]()
![]()
![]() -
- ![]()
=![]() -
- ![]() =0
=0
∴![]() -
- ![]()
例20:求与向量![]() =
=![]() 共线且满足方程
共线且满足方程![]() =-18的向量
=-18的向量![]() 。
。
解:因为![]() 与
与![]() 共线
共线
所以![]() =
=![]()
![]() =
=![]() ,其中
,其中![]() 为非零常数
为非零常数
又因为![]() =-18
=-18
所以![]() ·
·![]() =-18
=-18
从而4![]() +
+![]() +4
+4![]() =-18
=-18![]()
![]() =-2
=-2
所以x=![]()
5.投影
如上图,![]() ,
,![]() ,
,![]() ,S是点R在直线PQ上的垂足,那么
,S是点R在直线PQ上的垂足,那么![]() 就称为向量
就称为向量![]() 在向量
在向量![]() 上的投影向量,记为
上的投影向量,记为![]() ,数值
,数值![]() 称为向量
称为向量![]() 在向量
在向量![]() 上的投影,也可称为向量
上的投影,也可称为向量![]() 在向量
在向量![]() 方向上的分量。
方向上的分量。
当![]() 时,数值
时,数值![]() >0;
>0;
当![]() 时, 数值
时, 数值![]() <0;
<0;
当![]() 时,数值
时,数值![]() =0。
=0。
由于![]()
![]() ,因此,
,因此,![]() 的数量积又可解释为向量
的数量积又可解释为向量![]() 在向量
在向量![]() 上的投影与
上的投影与![]() 的模的乘积。
的模的乘积。
所以向量![]() 在向量
在向量![]() 上的投影可由
上的投影可由![]() 与
与![]() 方向上的单位向量作点乘而得到。
方向上的单位向量作点乘而得到。
设![]() ,
,
因为![]() ,
,![]() ,
,![]()
所以![]() 的三个分量正是
的三个分量正是![]() 在三个坐标轴上的投影。
在三个坐标轴上的投影。
例21:已知![]() ={1,1,-4},
={1,1,-4},![]() ={1,-2,2},求
={1,-2,2},求
(1)![]() ·
·![]() ; (2)
; (2)![]() 与
与![]() 的夹角; (3)
的夹角; (3)![]() 在
在![]() 上的投影。
上的投影。
解:(1)![]() ·
·![]() ={1,1,-4}·{1,-2,2}=1·1+1·(-2)+(-4)·2=-9
={1,1,-4}·{1,-2,2}=1·1+1·(-2)+(-4)·2=-9
(3) ![]()
![]() ·
·![]() =
=![]() ·projb
·projb![]() ∴ projb
∴ projb![]() =
=![]() =-3
=-3
7.4.2 两向量的向量积
两个向量除了作数量积以外,还可以作所谓的“向量积”运算,向量积的结果是一个向量而不是一个数。但值得注意的是,数量积运算在二维与三维空间均可定义,而“向量积”运算仅仅定义在三维空间中。
1、两向量的向量积定义
定义 设向量![]() 是由两个向量
是由两个向量![]() 与
与![]() 按下列方式定出:
按下列方式定出:
![]() 的模
的模![]() ,其中
,其中![]() 为
为![]() 与
与![]() 间的夹角;
间的夹角;
![]() 的方向垂直于
的方向垂直于![]() 与
与![]() 所决定的平面(即
所决定的平面(即![]() 既垂直于
既垂直于![]() ,又垂直于
,又垂直于![]() ),
),![]() 的指向按右手规则来确定,即:四个手指首先指向
的指向按右手规则来确定,即:四个手指首先指向![]() 的方向,再从
的方向,再从![]() 的方向转向
的方向转向![]() 的方向,则大拇指所指的方向就是
的方向,则大拇指所指的方向就是![]() 的方向。
的方向。
那末,向量![]() 叫做向量
叫做向量![]() 与
与![]() 的向量积,记作
的向量积,记作![]() ,即
,即
![]()
由向量积的定义可以推得:
(1)![]()
(2)对于两个非零向量![]() 与
与![]() ,如果
,如果![]() =0,那末
=0,那末![]() ;反之,如果
;反之,如果![]() ,那末
,那末![]() =0。
=0。
事实上:如果![]() =0,由于
=0,由于![]() ,
,![]() ,故必有
,故必有![]() ,
,
则![]() 或
或![]() ,即
,即![]() ;
;
2、向量积符合下列运算规律
(1)![]()
这是因为按右手规则从![]() 转向
转向![]() 定出的方向恰好与按右手规则从
定出的方向恰好与按右手规则从![]() 转向
转向![]() 定出的方向相反。它表明交换律对向量积不成立。
定出的方向相反。它表明交换律对向量积不成立。
(2)分配律:![]()
(3)结合律:![]() (λ为常数)。
(λ为常数)。
3、向量积的坐标表示式
设![]() ,
,![]() 。
。
那末,按上述运算规律,得
![]()
![]()
![]()
![]()
=![]()
![]()
![]()
![]()
由于![]() ,
,
![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
所以![]()
为了帮助记忆,利用三阶行列式,上式可写成
![]()
关于三阶行列式的计算参考实时讲解。
例26:设![]() ,
,![]() ,计算
,计算![]() 。
。
解:
例27:已知三角形ABC的顶点分别是![]() 、
、![]() 和
和![]() ,求三角形ABC的面积。
,求三角形ABC的面积。
解:根据向量积的定义,可知三角形ABC的面积
由于![]() ,
,![]() ,因此
,因此
§7.5 平面及其方程
7.5.1 平面的点法式方程
如果一非零向量垂直于一平面,这个向量就叫做该平面的法线向量,简称法向量。平面上的任一向量均与该平面的法向量垂直。
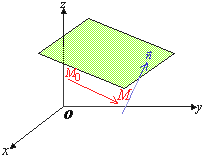
因为过空间一点可以作而且只能作一平面垂直于一已知直线,所以当平面Π上一点![]() 和它的一个法线向量
和它的一个法线向量![]() 为已知时,平面Π的的位置就完全确定了。下面我们来建立平面Π的方程。
为已知时,平面Π的的位置就完全确定了。下面我们来建立平面Π的方程。
设![]() 是平面Π上的任一点(图7-9)。
是平面Π上的任一点(图7-9)。
那末平面Π上的向量![]() 必与平面Π的法线向量n垂直,
必与平面Π的法线向量n垂直,
即它们的数量积等于零:
![]()
由于![]() ,
,
![]() ,所以有
,所以有
![]() (1)
(1)
这就是平面Π上任一点M的坐标x、y、z所满足的方程。
反过来,如果![]() 不在平面Π上,那末向量
不在平面Π上,那末向量![]() 与法线向量
与法线向量![]() 不垂直,从而
不垂直,从而![]() ,即不在平面Π上的点M的坐标x、y、z不满足方程(1)。
,即不在平面Π上的点M的坐标x、y、z不满足方程(1)。
由此可知,平面Π上的任一点的坐标x、y、z都满足方程(1);不在平面Π上的点的坐标都不满足方程(1)。这样,方程(1)就是平面Π的方程,而平面Π就是方程(1)的图形。由于方程(1)是由平面Π上的一点![]() 及它的一个法线向量
及它的一个法线向量![]() 确定的,所以方程(1)叫做平面的点法式方程。
确定的,所以方程(1)叫做平面的点法式方程。
例28:求过点(2,-3,0)且以![]() 为法向量的平面的方程。
为法向量的平面的方程。
例29:求过三点![]() 、
、![]() 和
和![]() 的平面的方程。
的平面的方程。
例30:求过点![]() 且垂直于平面
且垂直于平面![]() 和
和![]() 的平面方程。
的平面方程。
例31:设一平面经过原点及点![]() ,且与平面
,且与平面![]() 垂直,求此平面方程。
垂直,求此平面方程。
7.5.2 平面的一般式方程
由于平面的点法式方程(1)是x、y、z的一次方程,而任一平面都可以用它上面的一点及它的法向量来确定,所以任一平面都可以用三元一次方程来表示。
反过来,设有三元一次方程
![]() (2)
(2)
我们任取满足该方程的一组数![]() ,即
,即
![]() (3)
(3)
把上述两等式相减,得
![]() (4)
(4)
把它和平面的点法式方程(1)作比较,可以知道方程(4)是通过点![]() 且以
且以![]() 为法向量的平面方程。但方程(2)与方程(4)同解,这是因为由(2)减去(3)即得(4),又由(4)加上(3)就得(2)。由此可知,任一三元一次方程(2)的图形总是一个平面。方程(2)称为平面的一般方程,其中x、y、z的系数就是该平面的一个法向量n的坐标,即
为法向量的平面方程。但方程(2)与方程(4)同解,这是因为由(2)减去(3)即得(4),又由(4)加上(3)就得(2)。由此可知,任一三元一次方程(2)的图形总是一个平面。方程(2)称为平面的一般方程,其中x、y、z的系数就是该平面的一个法向量n的坐标,即![]() 。
。
例如,方程![]()
表示一个平面,![]() 是这平面的一个法向量。
是这平面的一个法向量。
对于一些特殊的三元一次方程,应该熟悉它们的图形的特点。
当D=0时,方程(2)成为![]() ,它表示一个通过原点的平面(见右图)。
,它表示一个通过原点的平面(见右图)。
当A=0时,方程(2)成为![]() ,法向量
,法向量![]() 垂直于x轴,方程表示一个平行于x轴的平面(见右图)。
垂直于x轴,方程表示一个平行于x轴的平面(见右图)。
同样,方程![]() 和
和![]() ,分别表示一个平行于y轴和z轴的平面。
,分别表示一个平行于y轴和z轴的平面。
当A=B=0时,方程(2)成为或![]() ,法向量
,法向量![]() 同时垂直x轴和y轴,方程表示一个平行于xOy面的平面(见右图)。
同时垂直x轴和y轴,方程表示一个平行于xOy面的平面(见右图)。![]()
同样,方程![]() 和
和![]() 分别表示一个平行于yOz面和xOz面的平面(见下图)。
分别表示一个平行于yOz面和xOz面的平面(见下图)。
例32:设平面经过原点及点![]() ,且与平面
,且与平面![]() 垂直,求此平面方程。
垂直,求此平面方程。
例33:求通过x轴和点(4,-3,-1)的平面的方程。
例34:设一平面与x、y、z轴的交点依次为![]() 、
、![]() 、
、![]() 三点,求这平面的方程(其中
三点,求这平面的方程(其中![]() ,
,![]() ,
,![]() )。
)。
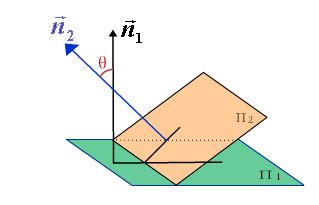
7.5.3 两平面的夹角
定义 两张平面的法向量的夹角(通常指锐角)称为两平面的夹角。
设平面Π1和Π2为:
![]()
![]()
它们的法向量依次为:
![]() 、
、![]() ,
,
记平面Π1和Π2的夹角![]() ,由规定
,由规定![]() 应是锐角,因此
应是锐角,因此![]() 的余弦值非负。
的余弦值非负。
![]()
从两向量垂直、平行的充分必要条件立即推得下列结论:
两张平面Π1、Π2互相垂直的充分必要条件是:![]() ;
;
例35:研究以下各组里两平面的位置关系:
(1)![]()
(2)![]()
(3)![]()
例36:求两平面![]() 和
和![]() 的夹角。
的夹角。
例37:一平面通过两点![]() 和
和![]() 且垂直于平面
且垂直于平面![]() ,求它的方程。
,求它的方程。
解:
设所求平面的一个法向量为:![]()
![]() 在所求平面上,它必与
在所求平面上,它必与![]() 垂直,
垂直,
所以有![]() (7)
(7)
又因所求的平面垂直于已知平面![]() ,所以又有
,所以又有
![]() (8)
(8)
由(7)、(8)得到
![]()
![]()
由平面的点法式方程可知,所求平面方程为
![]()
将![]() 及
及![]() 代入上式,并约去
代入上式,并约去![]() ,便得
,便得
![]()
或![]() ,这就是所求的平面方程。
,这就是所求的平面方程。
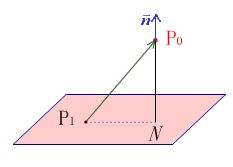
例38:设![]() 是平面π:
是平面π: ![]() 外一点,求P0到这平面的距离。
外一点,求P0到这平面的距离。
解:
过点![]() 作平面π的垂线,设垂足为N,则所求距离为
作平面π的垂线,设垂足为N,则所求距离为![]() ,在平面上任取一点
,在平面上任取一点![]() ,并作一法向量
,并作一法向量![]() ,由图,知所求的距离为:
,由图,知所求的距离为:
![]()
设![]() 为与向量
为与向量![]() 方向一致的单位向量,那末有
方向一致的单位向量,那末有
Prjn![]() =
=![]() ·
·![]()
而
![]()
![]()
所以
由于![]()
由此得点![]() 到平面
到平面![]() 的距离公式:
的距离公式:
例如,求点(2,1,1)到平面![]() 的距离,可利用公式(9),便得
的距离,可利用公式(9),便得
§7.6 直线及其方程
7.6.1 空间直线的一般方程
空间直线L可以看作是两个平面Π1和Π2的交线。如果两个相交的平面Π1和Π2的方程分别为:
Π1:![]()
Π2:![]() ,
,
那末直线L上的任一点的坐标应同时满足这两个平面的方程,即应满足方程组
反过来,如果点M不在直线L上,那末它不可能同时在平面Π1和Π2上,所以它的坐标不满足方程组(1)。因此,直线L可以用方程组(1)来表示。方程组(1)叫做空间直线的一般方程。
通过空间一直线L的平面有无限多个,只要在这无限多个平面中任意选取两个,把它们的方程联立起来,所得的方程组就表示空间直线L。由此可知,三元一次方程组表示空间直线。