【编译原理】中间代码优化(二) 局部优化

预备知识简述.

对于一个给定的程序，我们可以把它划分为一系列的基本块。在各个基本块范围内，分别进行优化。局限于基本块范围内的优化称为基本块内的优化，或者称为局部优化。

所谓基本块，是指程序中一个顺序执行的语句序列，其中只有一个入口和一个出口。入口就是其中的第一个语句。对于一个基本块来说，执行时只能从其入口进入，从其出口退出。

下面的三地址码序列就构成了一个基本块：
T1:=a*a
T2:=a*b
T3:=2*T2
T4:=T1+T2
T5:=b*b
T6:=T4+T5
如果一条三地址码语句为x:=y+z，则称对x定值并引用y和z。对于基本块内的某个名字和某个给定点，如果在程序中(包括在本基本块和其他基本块)这个名字在这个点以后被引用，我们就称这个名字在这个给定点是活跃的。

划分基本块の算法.

1. 首先要求出四元式程序中各个基本块的入口语句，它们是：
   a).程序的第一个语句；
   b).能由条件转移语句或无条件转移语句转移到的语句；
   c).紧跟在条件转移语句后面的语句。
2. 对以上求出的每一入口语句，构造其所属的基本块。基本块是由该入口语句A到另一入口语句B(不包括语句B)，或者到一条转移语句C(包括语句C)，或者到一条停语句D(包括语句D)之间的语句序列组成的；
3. 凡未被纳入某一个基本块中的语句，都是程序中控制流无法到达的语句，所以这些语句也是不会执行到的，我们完全可以把他们从程序中删除。

介绍完了划分基本块的算法之后，我们用一个例子来具体地看看算法执行的过程和结果：

【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】

根据算法流程，第一步先找出入口语句，它们分别是第1、4、6、8，我们在下一张图中用红色序号标明。

【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】

下一步是构造每一个入口语句的基本块。对于语句1来说，它的基本块范围只能到3号语句，因为4号语句是另一个入口语句了。对于语句4来说，它的基本块范围是[4…5]，因为6号语句是另一个入口语句。[6…7]基本块的划分方法与上面同理，而8号语句遇到halt语句才完成了自己基本块的构造。综上，上面的四元式代码序列，划分出来4个基本块：[1…3]、[4…5]、[6…7]和[8…9]，如下图所示：

【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】

基本块内可以实现の优化.

除了我们在中间代码优化(一)中介绍过的删除多余运算以及删除无用赋值两种技术外，基本块内还可以实现下列优化操作。

1.合并已知量.

假设在一个基本块内有下面这样的语句：
T:=2
...
S=2*T
如果在对T赋值以后没有改变过，则S=2*T中的两个运算对象也都是在编译时的已知量，那么就可以在编译时计算出S的值，而不必等到程序运行时才计算。也就是说可以把上面基本块中的最后一句变换为S=4，这样的变换叫做合并已知量。

2.临时变量改名.

假设在一个基本块内有语句T=b+c，其中T是一个临时变量名，那么如果我们将这一语句改为S=b+c并且将整个基本块中所有出现T的地方都改成S，则不改变基本块的值。事实上，总可以将一个基本块变换成另一个等价的基本块，是其中定义临时变量的语句改成定义新的临时变量。

3.交换语句位置.

假设在一个基本块里有下列两个相邻的语句：T=b+c;S=x+y，并且x、y均不为T，b、c均不为S，那么交换这两个语句的顺序并不会影响基本块的执行结果。有时候我们通过交换语句的次序，可以产生出更加高效的代码。

4.代数变换.

代数变换的具体含义是对于基本块中的求值表达式，用代数上等价的形式替换，目的是将复杂的运算变成简单的运算。很有名的秦九韶公式(Horner’s Rule)就是一种代数等价的变换，将多项式求值变得很高效率。例如语句x=x+0;y=y*1中的运算并没有执行的意义，可以从基本块中删除；再比如x=y**2中的幂运算，通常需要调用函数来实现，通过代数变换，可以用x=y*y来代替。

程序流图.

通过构造一个有向图，我们称之为流图。在这个图中我们可以将程序的控制流信息附加到图的有向边上，从而表示一个程序。流图以基本块为结点，那个以程序的第一条语句为入口语句的基本块作为首结点。如果在某个执行顺序中，基本块B${}_2$紧接在基本块B${}_1$之后执行，则从B${}_1$到B${}_2$有一条有向边。也就是说如果：

1. 有一个条件(无条件)转移语句从B${}_1$的最后一条语句转移到B${}_2$的第一条语句，或者；
2. 在程序的序列中，B${}_2$紧跟在B${}_1$之后，并且B${}_1$的最后一条语句不是一个无条件转移语句

我们就说B${}_2$是B${}_1$的后继，而B${}_1$是B${}_2$的前驱。前面我们给出的基本块划分算法中的实例中，就是一个程序流图的例子。控制流图的优势在于，它可以清晰地表示出三地址码所不能表征的控制流信息，从而有助于我们进行控制流、数据流分析。从本质上来说，控制流图也是一种中间代码。

DAG表示及其应用.

DAG是Directed Acyclic Graph的首字母缩略词，意为有向无环图。基本块的DAG表示，是一种图中结点带有标记或附加信息的形式。标记可以有下述的三种：

1. 图的叶结点以一标识符(变量名)或常数作为标记，表示该结点代表了这个变量或常数的值。如果需要叶结点表示某个变量A的地址，则使用addr(A)作为这个结点的标记。有些叶结点上的标记有下标0，代表它是这个变量的初值。
2. 图的内部结点以一运算符作为标记，表示该结点代表使用这一运算符，并将其后继结点代表的值作为操作数而获得的运算结果。
3. 图中的结点可能附加一个或多个变量标识符，这意味着这些变量都具有该结点所代表的值。

我们先看一个DAG图的实例，对其有一个宏观的印象，再介绍代码基本块的DAG构造算法。

(1)T0:=3.14
(2)T1:=2*T0
(3)T2:=R+r
(4)A:=T1*T2
(5)B:=A
(6)T3:=2*T0
(7)T4:=R+r
(8)T5:=T3*T4
(9)T6:=R-r
(10)B:=T5*T6

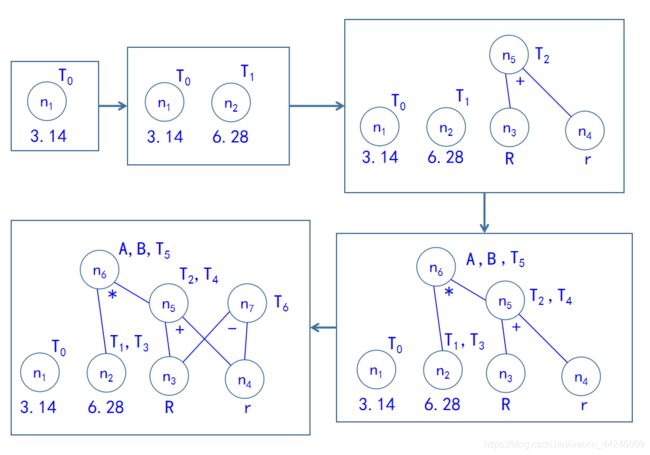
【上图引用自中南大学徐德智老师的编译原理2020年授课PPT】
图中是这个四元式代码序列对应的DAG图构建过程，最终的DAG图展示如下：

【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】

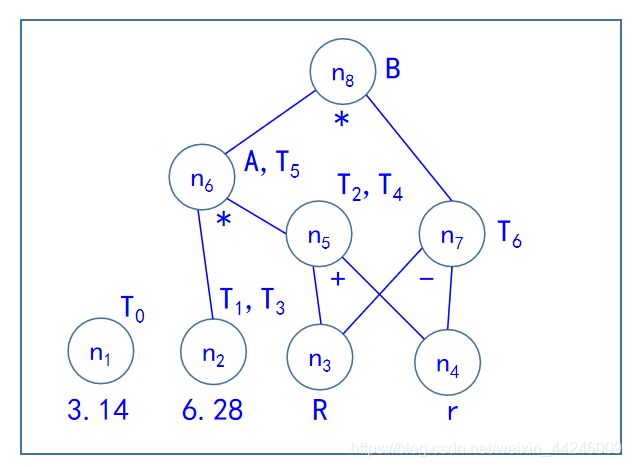
我们可以对照上面给出的标记信息的解释，来理解一下每个结点所代表的值、意义以及对应了哪一条三地址码语句。

DAG构造算法.

假设DAG各结点的信息将采取某种适当的数据结构来存放，例如链表。并且设有一个标识符(当中包括常数)与结点的对应表，NODE(A)是描述这种对应关系的一个函数，它的返回值或者是一个结点编号n，或者没有返回值。当NODE(A)=n时，意味着DAG中存在一个结点n，它的标记或者附加标识符是A。
我们讨论的中间代码形式，只限于以下三种：

0. A:=B
1. A:=op B
2. A:=B op C 或 A:=B[C]

基于以上假定，我们给出基本块的DAG构造算法。

0. 初始化，DAG=NULL. 考察基本块中的每一条中间代码，依次执行以下步骤；
1. 如果NODE(B)无定义，则构造一个标记为B的叶结点，并且定义NODE(B)的返回值是这个结点。①如果当前代码是(0)型A:=B，则记NODE(B)的值为n，跳转到第四步；②如果当前代码是(1)型A:=op B，则跳转到第二步的第一分支；③如果当前代码是(2)型，并且如果NODE(C)无定义，那么就构造一个标记为C的叶结点并且定义NODE(C)的返回值是这个结点，跳转到第二步的第二分支。
2. ①如果NODE(B)是标记为常数的叶结点，则跳转到第二步的第三分支，否则跳转到第三步的第一分支；②如果NODE(B)和NODE(C)都是标记为常数的叶结点，则跳转到第二步的第四分支，否则跳转到第三步的第二分支；③执行op B(合并已知量)，令得到的新常数为k. 如果NODE(B)是处理当前代码新构造出来的结点，则删除它。如果NODE(k)无定义，则构造一个以k为标记的叶结点。置NODE(k)=n，跳转到第四步。④执行B op C(合并已知量)，令得到的新常数为k. 如果NODE(B)或NODE©是处理当前代码新构造出来的结点，则删除它。如果NODE(k)无定义，则构造一个以k为标记的叶结点。置NODE(k)=n，跳转到第四步。
3. ①检查DAG中是否已经存在一个结点，它的唯一后继为NODE(B)并且标记为op(查找公共子表达式)，如果没有则构造结点n，否则就把已有的结点作为它的结点并设该结点为n。跳转到第四步。②检查DAG中是否已经存在一个结点，它的左后继为NODE(B)，右后继为NODE(C)，并且标记为op(查找公共子表达式)，如果没有则构造结点n，否则就把已有的结点作为它的结点并设该结点为n。跳转到第四步。
4. 如果NODE(A)无定义，则把A附加在结点n上并令NODE(A)=n；否则先把A从NODE(A)结点上的附加标识符集中删除(如果NODE(A)是叶结点，则不用删除A)，把A附加到新的结点n上，并令NODE(A)=n。
5. 跳转回第一步，继续处理下一条代码。

接下来我们以上面示例中的三地址码序列作为实例，来模拟一次DAG构造算法的执行。

(1)T0:=3.14
(2)T1:=2*T0
(3)T2:=R+r
(4)A:=T1*T2
(5)B:=A
(6)T3:=2*T0
(7)T4:=R+r
(8)T5:=T3*T4
(9)T6:=R-r
(10)B:=T5*T6

1. T0:=3.14，作为(0)型代码，根据算法中的步骤，在第1步中先构造NODE(B)，并将它的值标记为n，然后跳转到第4步，将T0附加在构造出的结点n上，得到下面这个DAG：
   
   【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】
   

2. T1:=2*T0，作为(2)型代码，先构造出标记为常数2的结点，因为NODE(T0)已经存在，就跳转到第2步的第二分支。由于标记2和标记3.14都是常数，所以再跳转到第2步的第四分支，执行2*T0的运算，构造出以6.28为标记的结点NODE(k)，并且由于NODE(2)是当前语句生成的结点，所以需要删除以NODE(2)，跳转到第4步。因为NODE(T1)无定义，所以将T1附加到这个结点上，最后生成下示的DAG图：
   
   【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】
   

3. T2:=R+r，作为(2)型代码，首先构造NODE(R)，再构造NODE(r)，跳转到第2步的第二分支，由于R和r都不是常数，所以跳转到第3步的第二分支。查找发现DAG中并没有左后继为NODE(R)，右后继为NODE(r)的结点，所以构造这样的一个结点n，跳转到第4步，将T2附加在结点n上，得到下面的DAG图：
   
   【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】
   

4. A:=T1*T2，作为(2)型代码，通过算法的流程到达第3步的第二分支，查找发现并没有左后继为NODE(T1)，右后继为NODE(T2)的结点，于是构造一个这样的结点n，在第4步中将A附加到结点n的标记上，得到这样的DAG图：
   
   【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】

5. [5…8]的三地址码序列，都是以及存在的结点，只要将标识符附加到既有的结点上即可，DAG如下：
   
   【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】
   

6. T6:=R-r的构造过程和T2:=R+r类似，区别在于T6这一语句构造时R和r的结点已经存在了，所以只需要构造标记为-的内部节点；B:=T5*T6的构造过程和A:=T1*T2一致，需要注意的是在第四步中要将原本附加在NODE(A)结点上的标记B删去，重新附加在T5*T6的结点上，最终的DAG图如下：
   
   【下图引用自中南大学徐德智老师的编译原理2020年授课PPT】
   

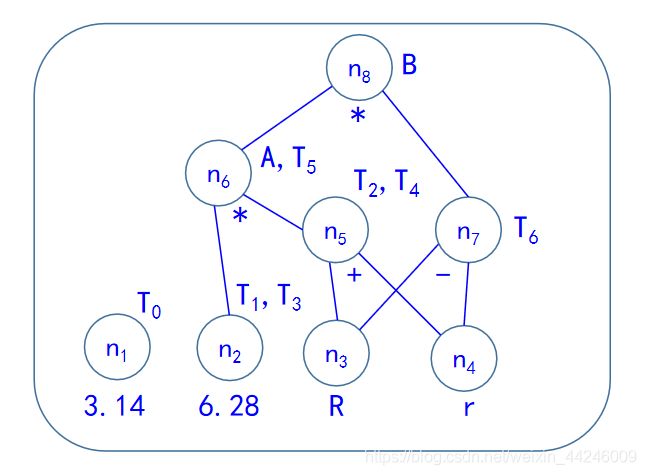
通过上面的例子，我们可以得到下面的一些结论：

1. 对于任何一句代码，如果其中的运算量都是编译时的已知量，那么DAG中并不会生成其内部节点，而是直接进行运算，将结果(也是常数)作为一个标记生成叶结点。例如我们T1:=2*T0的构造过程，可以看出步骤2的作用就是合并已知量。
2. 算法的步骤3是查找公共子表达式，对具有公共子表达式的代码，DAG算法只产生一个计算该表达式值的内部结点，而将那些被赋值的变量直接附加在这唯一的结点上。例如我们T3:=2*T0这样代码的构造过程。
3. 如果某个变量被赋值后，在它被引用前又被重新赋值，那么算法的步骤4能够将其从前一个值的结点上删除，也就是说步骤4有删除无用赋值的作用。

因此我们可以利用这样的DAG来重新生成原基本块的，一个经过了优化的中间代码序列。

DAG与基本块の优化.

如果DAG的某个内部结点上附有多个标识符，说明计算该结点值的表达式是一个公共子表达式，当我们将该结点重新写成中间代码时，就可以实现删除多余运算，所以按照这样的思想，我们可以根据DAG写出下面的中间代码：

(1)T0:=3.14
(2)T1:=6.28
(3)T3:=6.28
(4)T2:=R+r
(5)T4:=T2
(6)A:=6.28*T2
(7)T5:=A
(8)T6:=R-r
(9)B:=A*T6

这段代码就是对最初的中间代码实现了合并已知量、删除多余运算、删除无用赋值三种优化后的结果。除了可以应用DAG进行基本块的优化之外，我们从DAG中还能得出下列信息：

• 在基本块之外被定值，并且在基本块内被引用的所有标识符，就是DAG图中叶结点上标记的那些标识符；
• 在基本块内被定值，并且定值之后能够被引用的所有标识符，就是DAG图中内部结点上附加的那些标识符。

利用这些信息，我们还可以进一步地删除中间代码中的无用赋值，但这需要获取有关变量在基本块后面被引用的情况(数据流分析)。如果DAG中某个结点上附加的标识符在后面并没有被引用，那么就不生成对该标识符的赋值语句；又如某个结点上不附有任何标识符或者上面附加的标识符在后面不被引用，而且它也没有前驱结点，这就意味着基本块内以及基本块之后都不会引用该结点的值，那么就可以不生成该结点的代码；再比如有这样的两条语句A=x op y;B=A并且第一条语句的结果A只在第二条语句被引用，那么完全可以将这两条语句合并为B=x op y.
我们现在假设，对于上面已经经过DAG优化的中间代码来说，T0,T1,T2,T3,T4,T5,T6在后面的代码都不会被引用，那么中间代码序列就可以写成下面的样子：

S1=R+r
A=6.28*S1
S2=R-r
B=A*S2

其中没有生成对T0,T1,T2,T3,T4,T5,T6赋值的语句，S1、S2是用于存放中间结果的临时变量。上述语句序列是根据结点的构造顺序[n${}_5$,n${}_6$,n${}_7$,n${}_8$]来生成的，如果我们采用其他顺序，并且保证任意结点的语句在其后继结点的语句之后、转移语句(如果有的话)仍然是基本块的最后一个语句即可。这里如果我们按照[n${}_7$,n${}_5$,n${}_6$,n${}_8$]的顺序来重写中间代码：

S1=R-r
S2=R+r
A=6.28*S2
B=A*S1

在目标代码生成部分，我们会看到后一种中间代码是优于前一种代码的，我们会介绍如何重排DAG的结点顺序以生成更加高效的目标代码。

复杂基本块.

我们前面在讨论DAG构造算法时，假定了代码种类只有三种：

1. A:=B
2. A:=op B
3. A:=B op C 或 A:=B[C]

然而当基本块中出现数组元素引用、指针以及过程调用时，情况就复杂起来。例如我们考察下列语句序列：

x=a[i]
a[j]=y
z=a[i]

如果我们头铁，不做变通地应用DAG构造算法，将a[i]视为公共子表达式，那么“优化”后的代码序列就会如下：

x=a[i]
z=x
a[j]=y

我们考虑i=j并且y≠a[i]的情况，这确实是存在的一种情况，那么上述"优化"前后的代码结果是不同的。问题的原因在于，当我们对一个数组元素赋值时，我们可能改变表达式a[i]的右值，即使a和i的值都没有改变。因此我们对数组a的一个元素赋值时，我们“注销”所有标记为[ ]、左边的变元是a加上或减去一个常数的结点。即我们认为对于这样的结点来说，再添加附加标识符是非法的，从而取消了它作为公共子表达式的资格。这一操作要求我们对每个结点设置一个标志位来标记该结点是否被“注销”。另外，对每个基本块中引用的数组a，我们可以保存一个节点表，当中的内容是当前未被注销，但若有对a中一个元素赋值则必须被注销的结点。
对指针赋值*p=w，其中p是一个指针会产生同样的问题。如果我们不知道p指向哪一个变量，就要认为它可能指向基本块中的任何一个变量。当构造这种赋值语句的结点时，要将DAG中各结点上所有标识符(包括叶结点标识符)都予以注销。将DAG中所有结点上的标识符都注销，也同时意味着DAG中的所有结点都被注销。
在一个基本块中的一个过程调用将注销所有的结点，因为对被调用过程的情况缺乏了解，我们必须假定任何变量都可能因为副作用而发生变化。
在DAG与基本块の优化中我们提到过，可以不按照DAG结点的构造顺序来重写代码，这种操作就必须注意DAG中的某些结点一定要遵守某种顺序。我们根据上面对于数组元素、指针以及过程调用情况的本来意义，将重写中间代码时DAG结点之间必须遵守的顺序归纳如下：

1. 对于数组a任何元素的引用或赋值，都必须跟在原来位于其前面(如果有的话)对于数组a任何元素的赋值之后；
2. 对于数组a任何元素的赋值，都必须跟在原来位于其前面(如果有的话)对于数组a任何元素的引用之后；
3. 对于任何标识符的引用或赋值，都必须跟在原来位于其前面的任何过程调用或通过指针进行的间接赋值之后；
4. 任何过程调用或通过指针进行的间接赋值，都必须跟在原来位于其前面的对于任何标识符的引用或赋值之后。

总结来说就是，当重写基本块时，任何数组a 的引用不可以互相调换次序，并且任何语句不得跨越一个过程调用语句或者一个通过指针的间接赋值语句。