数值分析之三角分解法求线性方程组
@数值分析之线性方程组AX=B求解
文章目录
- 一、三角分解法
- 1.1 三角分解法
- 1.2 matlab算法
- 二、题目
- 2.1 题目
- 2.2 输入输出格式
- 2.3 样例
- 输入
- 输出
- 2.4 思路和要点
- 2.5 代码
- 2.6 结果
一、三角分解法
问:高斯偏序选主元、上三角回代解法已经可以解一切线性方程组,为什么还要三角分解法呢?
答:如果是单独处理一个方程组,三角分解和高斯分解的区别只是,三角分解保存了分解因子。但如果多次求解某个系数矩阵A相同,列矩阵B不同的方程组,就省去三角分解过程。同时A可以直接使用,节省了资源。
1.1 三角分解法
三角分解法:A = LU,AX=B,即LUX=B,令Y=UX,即LY=B,先前向替代求解Y,在回代求解X。该算法关键是将A拆分为下三角L(L(k,k)=1)和上三角U的矩阵乘,在分解A的过程中,将分解因子L、U保存在一个矩阵R中,只保存L的非0非1部分,U的非0部分。
为了避免和高斯消去同样的问题,三角分解法也采用偏序选主元策略,只是在变换A的过程中,还要保存行变换信息
1.2 matlab算法
二、题目
2.1 题目
为求解一个线性方程组,首先采用偏序选主元策略的三角分解法构造矩阵L,U和P,再用前向替换法对方程组LY=PB求解Y,最后用回代法对方程组UX=Y求解X。
2.2 输入输出格式
【输入形式】在屏幕上依次输入方阵阶数n,系数矩阵A和常数矩阵B。
【输出形式】先输出LU分解结果,再输出方程解。
2.3 样例
输入
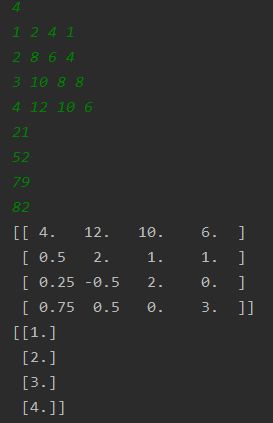
4
1 2 4 1
2 8 6 4
3 10 8 8
4 12 10 6
21
52
79
82
输入说明:输入:第1行为方阵阶数4,第2行至5行为系数矩阵A,第6行至9行为常数矩阵B。
输出
[[ 4. 12. 10. 6. ]
[ 0.5 2. 1. 1. ]
[ 0.25 -0.5 2. 0. ]
[ 0.75 0.5 0. 3. ]]
[[1.]
[2.]
[3.]
[4.]]
输出说明:第1至第4行输出LU分解结果,,第5行至第8行依次输出方程解:x1, x2, x3, x4。
2.4 思路和要点
(1)要注意,三角分解法与高斯消去不同。高斯分解采用偏序选主元时,是对[A|B]增广矩阵变换,而三角分解法只对A行交换。所以在A交换行时,要保存交换行索引,便于解下三角矩阵时,找到B中的对应行。
(2)三角分解的核心在于构建这个分解因子——两个三角矩阵,在代码中,我将两个矩阵合在了一个矩阵中,也就是LU分解结果。只保存了上三角非0的部分和下三角中非1非0的部分。同时因为互不干扰,为了节省内存,可以将LU保存在A上。
2.5 代码
import numpy as np
def lufact(A,R):
n = len(A)
for i in range(n):# 对i列处理
row = np.argmax(abs(A[i:,i]))
A[[i, row+i], :] = A[[i+row, i], :]
R[i],R[row+i] = R[row+i],R[i]
#因为交换的只是系数矩阵A的行,所以将A中行交换的信息保存,使得与B匹配
#每次交换行并不影响X的值的顺序,保证了backsub时不用考虑行交换
for k in range(i+1,n): #对第k行处理
m = A[k,i]/A[i,i]
A[k,i] = m
temp = m*A[i,i+1:]
A[k,i+1:] =A[k,i+1:] - temp
return A
def forsub(A,B,R,Y):#下三角前向替代
n = len(Y)
Y[0] = B[R[0]]
for i in range(1,n):
temp = np.reshape(A[i,0:i],(1,len(Y[0:i]))).dot(Y[0:i])
Y[i] = B[R[i]]-temp
return Y
def backsub(A, X): #上三角回代求解
#因为每一位处理后的Y都能得到对应位的x,所以可以在X矩阵中替换,节省资源
n = len(X)
X[n - 1] = X[n - 1] / A[n - 1, n - 1]
for i in range(n - 2, -1, -1):
temp = np.reshape(A[i, i + 1:], (1, len(X[i + 1:]))).dot(X[i + 1:])
# 截断的A虽然看似可以和X想点乘,但是程序会判断为形状不同,所以要重新赋予形状
X[i] = (X[i] - temp) / A[i, i]
return X
def main():
n = int(input())
A = np.zeros([n,n],dtype = np.double)
B = np.zeros([n,1],dtype = np.double)
X = np.zeros([n,1],dtype = np.double)
R = np.arange(n) #A发生行交换后保存交换的行索引,使得与B匹配
for i in range(n):
A[i,:] = np.array(input().split(),dtype = np.double)
for i in range(n):
B[i] = np.array(input(),dtype = np.double)
lufact(A,R)
forsub(A,B,R,X)
backsub(A,X)
print(A)
print(X)
if __name__ == '__main__':
main()