Educational Codeforces Round 5 ABCDE

Problem A

位数少的前面补零，比字典序，注意本身可能有前导0

#include
#include
#include
#include
#include
#include
#include
#include

---

Problem B

找每行的最小值，取每行最小值的最大值即可

#include
#include
#include
#include
#include
#include
#include
#include

---

Problem C

bfs白块并标记掉下次不再遍历，每次bfs记录白块的数量并统计所有本次bfs撞到的实心块，本次统计得到的白块数量加到每一个撞到的实心块的答案中

#include
#include
#include
#include
#include
#include
#include
#include
q;
char mp[N][N];
bool again[N][N];

void BFS(int stx,int sty)
{
    int cnt = 0;
    while (!q.empty()) q.pop();
    q.push({stx,sty});
    vis[stx][sty] = true;
    while (!q.empty()){
        P now = q.front();
        q.pop();
        cnt++;
        for0(i,0,4){
            int nowx = now.fi+dx[i];
            int nowy = now.se+dy[i];
            if (nowx<=0||nowx>n || nowy<=0||nowy>m) continue;
            if (mp[nowx][nowy]=='*'){
                if (again[nowx][nowy]) continue;
                getans.push({nowx,nowy});
                again[nowx][nowy] = true;
                continue;
            }
            if (mp[nowx][nowy]=='.' && !vis[nowx][nowy]) q.push({nowx,nowy}),vis[nowx][nowy]=true;
        }
    }
    while (!getans.empty()){
        P now = getans.front();getans.pop();
        again[now.fi][now.se] = false;
        ans[now.fi][now.se] += cnt;
    }
}

int main()
{
    while (~scanf("%d %d",&n,&m)){
        memset(vis,0,false);
        memset(ans,0,sizeof ans);
        for (int i=1;i<=n;i++) scanf("%s",mp[i]+1);

        for1(i,1,n){
            for1(j,1,m){
                if (mp[i][j]=='.' && !vis[i][j]) BFS(i,j);
            }
        }

        for1(i,1,n){
            for1(j,1,m){
                if (mp[i][j]=='.') printf(".");
                else printf("%d",(ans[i][j]+1)%10);
            }
            printf("\n");
        }

    }
    return 0;
}

---

Problem D

两个指针，一个指向起点，一个指向当前最远距离，第一个指针右移时第二个指针做出对应改变就行

#include
#include
#include
#include
#include
#include
#include
#include

---

Problem E

首先：f(n,m)表示n%1+....+n%m，那么有以下两种情况

n

n>=m,ans = f(n,n-1) + (m-n)*n

所以我们只需求m小于n的情况

对于f（n，m）公式化简：（CF原版题解截的图）

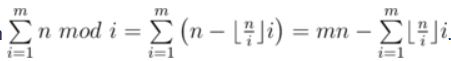
我们的任务就是求出[n/i]*i的前m项之和

我们发现当

n/2+1<=i<=n,时，[n/i] = 1

n/3+1<=i<=n/2时, [n/i]=2

n/x+1<=i<=n/(x-1)时，[n/i]=x-1

这意味着这意味这一段区间[n/i]都是一样的，只有i不同，可以直接整段一次求和。

利用这个性质我们把复杂度控制在O（sqrt（N））

可能有点分块的思想：

对于1~（n/sqrt（n））暴力计算

对于（n/sqrt（n）+1）~m 整段计算

这里有两个注意点：

①为什么分段点是n/sqrt（n）？

因为我把从[n/sqrt(n)+1,m]的区间整段计算，那么第一段左边界是 n/sqrt（n）+1，因为n一般不等于sqrt（n）*sqrt（n），所以这样不会出错也比较方便

②利用公式整段求和有除法取余操作，要用到逆元，否则出错。

逆元参考：https://blog.csdn.net/weixin_43768644/article/details/94768449

代码：（那个恶心的sum宏定义就是区间计算，以及除法变乘，逆元取模）

#include
#include
#include
#include
#include
#include
#include
#include

总结：

1.做不出跳题真的是个正确选择。

2.n！=sqrt（n）^2

3.BFS标记的时候想清楚，你要防止一个块因为扔进去的时候没有被标记导致被扔进去两次的情况，请在扔出来后判断有无标记或者扔进去的时候直接打标记。

4.数学题多推公式，找规律