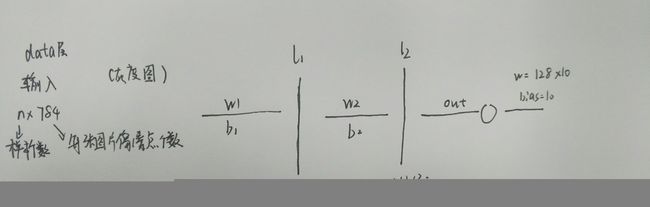
简单的双层神经网络训练mnist数据集
首先想要说明构建的这个神经网络的基本结构,还是利用mnist数据集进行训练,然后因为是最简单的神经网络,所以我们设定的网络结构是两层,然后第一层256个神经元,第二层是128个神经元,既然这样的话我们就可以计算出W1,W2,b1,b2的·个数。因为输入是784个,而第一层的神经元的个数是256个所以第一层的权重w的个数就是784*256,对应的应为第一层有256个神经元所以,对应L1有256个bias偏移值(b1)。同理可知第二层的神经元的参数为w:256*128,b:128,因为我们这是一个十分类的问题所以,我们输出应该是10纬的,所以,第二次层到输出层的w:128*10,b:10.
然后了解了结构之后,看一下具体的代码实现。、
首先是最基本的:
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import input_data
print ("packs loaded")mnist = input_data.read_data_sets('D:\pythonotebook\data', one_hot=True)
为了方便我直接把我的mnist数据集放在D盘的一个文件夹里面。所以直接取的这个位置。
然后就是神经网络结构的一些基本的搭建了
# NETWORK TOPOLOGIES
n_hidden_1 = 256 #第一层的神经元个数
n_hidden_2 = 128 #第二层的神经元个数
n_input = 784 #样本图片的像素点个数
n_classes = 10 #输出,或者说我们分的类别数
# INPUTS AND OUTPUTS
x = tf.placeholder("float", [None, n_input])#tensorflow提供了一个placeholder的函数,提供一个和能够放置n个包含m个像素点的容器,之后直接把值放进来即可
y = tf.placeholder("float", [None, n_classes])
# NETWORK PARAMETERS 这一步实际上就是参数框架的搭建
stddev = 0.1
weights = {
'w1': tf.Variable(tf.random_normal([n_input, n_hidden_1], stddev=stddev)),
'w2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2], stddev=stddev)),
'out': tf.Variable(tf.random_normal([n_hidden_2, n_classes], stddev=stddev))
}
biases = {
'b1': tf.Variable(tf.random_normal([n_hidden_1])),
'b2': tf.Variable(tf.random_normal([n_hidden_2])),
'out': tf.Variable(tf.random_normal([n_classes]))
}
print ("NETWORK READY")这里要说一下这里的代码:使用tf.random_normal这个函数来初始化我们的权重和偏移值,参数分为数目和高斯分布的标准差我们这里一开始就把这个值设置为0.01.之前的variable是tensorflow定义一个变量时候必须引用的函数。
上面的代码实际上完成的工作就是一个参数的初始化。
然后接下里啊我们需要定义一个神经网络训练的函数:
def multilayer_perceptron(_X, _weights, _biases):
layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(_X, _weights['w1']), _biases['b1']))
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, _weights['w2']), _biases['b2']))
return (tf.matmul(layer_2, _weights['out']) + _biases['out'])我们定义multilayer_perceptron这个函数然后这个函数有三个参数分别是你的输入,权重w,偏移值b
第一层的输出是要把w*x+b的值经过一个激活函数(这里采用sigmod函数),add是相加的意思,matmul是相乘的意思。
第二层的输入就是第一层的输出
然后我们把这个最中的输出结果返回(return函数)
# PREDICTION
pred = multilayer_perceptron(x, weights, biases)
# LOSS AND OPTIMIZER
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(pred, y))
optm = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost)
corr = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
accr = tf.reduce_mean(tf.cast(corr, "float"))
# INITIALIZER
init = tf.global_variables_initializer()
print ("FUNCTIONS READY")然后相当于我们通过上面定义的函数可以得到他的返回值(输出)然后把这个返回值赋给pred。
然后就是loss和精度的计算了
这里我们计算这个损失函数采用的是通过计算交叉熵,tensorflow里面给定了计算交叉熵的函数:tf.nn.softmax_cross_entropy_with_logits
通过我们的预测值(pred)和真实值就可以计算交叉熵了。
然后我们需要把这个损失降到最低,所以采用梯度下降法趋优化,同时,给定0.001的学习率。
之后就是计算精度了具体的精度计算的代码和我上一篇博客“逻辑回归分类mnist”一样,这里就不赘述了。
training_epochs = 100#我们采取迭代100步
batch_size = 100#么每次随机的选取100张
display_step = 4
# LAUNCH THE GRAPH 在tensorflow中做运算的时候都需要在一个session的容器中进行所以需要定义这个session
sess = tf.Session()
sess.run(init)
# OPTIMIZE
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples/batch_size)#这个num_examples是样本总数(55000),这里计算的是每次取100个,一共需要取多少次
# ITERATION
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)#next_batch这个函数可以实现一个个往下输入图像块的功能
feeds = {x: batch_xs, y: batch_ys}#需要导入进来的数据用字典定义。
sess.run(optm, feed_dict=feeds)
avg_cost += sess.run(cost, feed_dict=feeds)
avg_cost = avg_cost / total_batch#计算平均的损失
# DISPLAY
if (epoch+1) % display_step == 0:
print ("Epoch: %03d/%03d cost: %.9f" % (epoch, training_epochs, avg_cost))
feeds = {x: batch_xs, y: batch_ys}
train_acc = sess.run(accr, feed_dict=feeds)
print ("TRAIN ACCURACY: %.3f" % (train_acc))
feeds = {x: mnist.test.images, y: mnist.test.labels}
test_acc = sess.run(accr, feed_dict=feeds)
print ("TEST ACCURACY: %.3f" % (test_acc))
print ("OPTIMIZATION FINISHED")其他的代码和之前“逻辑回归分类mnist”中提到的一样,就不赘述了。
然后迭代一百次看看结果如下:
Epoch: 003/100 cost: 2.268264102
TRAIN ACCURACY: 0.180
TEST ACCURACY: 0.209
Epoch: 007/100 cost: 2.231292343
TRAIN ACCURACY: 0.310
TEST ACCURACY: 0.327
Epoch: 011/100 cost: 2.190411135
TRAIN ACCURACY: 0.500
TEST ACCURACY: 0.450
Epoch: 015/100 cost: 2.143339661
TRAIN ACCURACY: 0.610
TEST ACCURACY: 0.527
Epoch: 019/100 cost: 2.087858143
TRAIN ACCURACY: 0.590
TEST ACCURACY: 0.581
Epoch: 023/100 cost: 2.022166359
TRAIN ACCURACY: 0.560
TEST ACCURACY: 0.605
Epoch: 027/100 cost: 1.945109608
TRAIN ACCURACY: 0.590
TEST ACCURACY: 0.629
Epoch: 031/100 cost: 1.856792508
TRAIN ACCURACY: 0.660
TEST ACCURACY: 0.651
Epoch: 035/100 cost: 1.758972322
TRAIN ACCURACY: 0.630
TEST ACCURACY: 0.670
Epoch: 039/100 cost: 1.654991525
TRAIN ACCURACY: 0.620
TEST ACCURACY: 0.690
Epoch: 043/100 cost: 1.548811336
TRAIN ACCURACY: 0.640
TEST ACCURACY: 0.708
Epoch: 047/100 cost: 1.444407511
TRAIN ACCURACY: 0.680
TEST ACCURACY: 0.724
Epoch: 051/100 cost: 1.345108838
TRAIN ACCURACY: 0.760
TEST ACCURACY: 0.739
Epoch: 055/100 cost: 1.253329833
TRAIN ACCURACY: 0.750
TEST ACCURACY: 0.752
Epoch: 059/100 cost: 1.170350728
TRAIN ACCURACY: 0.750
TEST ACCURACY: 0.761
Epoch: 063/100 cost: 1.096484938
TRAIN ACCURACY: 0.780
TEST ACCURACY: 0.776
Epoch: 067/100 cost: 1.031252970
TRAIN ACCURACY: 0.710
TEST ACCURACY: 0.785
Epoch: 071/100 cost: 0.973843859
TRAIN ACCURACY: 0.810
TEST ACCURACY: 0.794
Epoch: 075/100 cost: 0.923228334
TRAIN ACCURACY: 0.810
TEST ACCURACY: 0.801
Epoch: 079/100 cost: 0.878521435
TRAIN ACCURACY: 0.740
TEST ACCURACY: 0.808
Epoch: 083/100 cost: 0.838815533
TRAIN ACCURACY: 0.820
TEST ACCURACY: 0.812
Epoch: 087/100 cost: 0.803438726
TRAIN ACCURACY: 0.770
TEST ACCURACY: 0.817
Epoch: 091/100 cost: 0.771740969
TRAIN ACCURACY: 0.840
TEST ACCURACY: 0.821
Epoch: 095/100 cost: 0.743218711
TRAIN ACCURACY: 0.800
TEST ACCURACY: 0.828
Epoch: 099/100 cost: 0.717470385
TRAIN ACCURACY: 0.840
TEST ACCURACY: 0.832
OPTIMIZATION FINISHED
迭代一百次的结果过发现精度可以达到0.83,损失可以达到0.7
但是相对于逻辑回归来说这个效果并不是非常的好,可能的原因是神经网络结构比较简单,同时迭代次数比较少。