论文阅读笔记|论文总结Automated Lesion Detection和PseudoEdgeNet两篇

文章链接
Automated Lesion Detection by Regressing Intensity-Based Distance with a Neural Network
PseudoEdgeNet: Nuclei Segmentation only with Point Annotations

Automated Lesion Detection by Regressing Intensity-Based Distance with a Neural Network

Motivation

病灶分割标注通常需要标注人员大量的专业知识和熟练度，耗费大量时间和成本，而且会因标注人员的差异性产生较大偏差。

Manual annotation of lesions can be challenging, time consuming and subject to observer bias.

Method

Distance Map

在一个灰度图像$G(x)$中，具有点标注集合$\Phi$，那么对于坐标点$x$，它的Distance Map为：

$$DM(x)=min(\Lambda (\gamma ),\gamma \in \Psi (x,\Phi ))$$

其中$\Psi (x,\Phi )$是标注点集到$x$所有路径$\gamma$的集合，而$\Lambda (\gamma )$则代表路径$\gamma$的长度：

$$\Lambda (\gamma )=\sum _{i=1}^{n-1}d(x_i,x_{i+1})$$

本文定义了三种路径距离度量方式，即三种Distance Map的计算方式。

欧几里得距离 Euclidean Distance

$$d_E(x_i,x_{i+1})=\{\begin{array}{ll}1,& x_{i+1}\in N_4(x_i)\\ \sqrt{2},& x_{i+1}\in N_8(x_i)-N_4(x_i)\end{array}$$

密度距离 Intensity Distance

$$d_I(x_i,x_{x+1})=G(x_i)-G(x_{i+1})$$

测地距离 Geodesic Distance

$$d_G(x_i,x_{i+1})=\sqrt{d_I(x_i,x_{x+1}{)}^2+d_E(x_i,x_{i+1}{)}^2}$$

三种路径度量方式获得Distance Map分别称为EDM，IDM和GDM。显然，EDM是$x$到最近的标注点的距离，IDM是$x$到强度差最小的标注点的强度差。最后对Distance Map做归一化。

$$M_p(x)=(1-\frac{DM(x)}{max(DM(x))}{)}^p$$

Network

使用U-net，MSE Loss function：

$$MSE=\frac{1}{N}\sum _x(M_p(x)-M_p(x){)}^2$$

Result

检测结果如下：

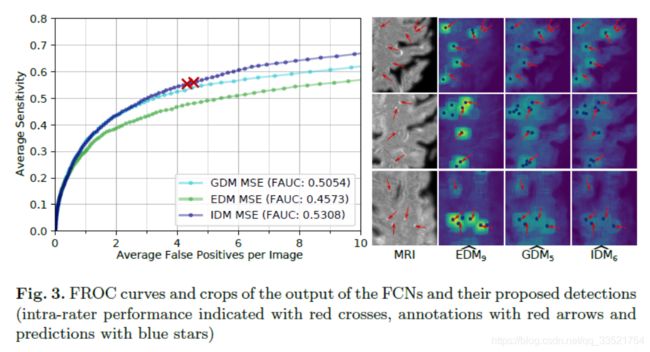
实际上可以看出效果不是很好，但是这种思路有可改进的地方。最简单的思路是two-phase，heatmap一定阈值对应的像素做一个二分类器。

PseudoEgdeNet: Nuclei Segmentation only with Point Annotations

Motivation

细胞核分割标注只能交给病理学家，因而耗时且昂贵。

Method

分割网络 $f$

损失函数使用binary cross-entropy。FPN with ResNet-50。

边缘网络 $g$

在CNN中，较浅的层提取低微信息，例如边缘与斑点。使用浅层的神经网络提取边缘，并将其与分割网络的Sober滤波结果计算loss。Sober算子是计算机图形中较为常用的边缘提取算子。4-layer CNN。

$$\mathcal{L}(I,P,f,g)={\mathcal{L}}_{ce}(f(I),P)+\gamma |s(f(I)-g(I))|$$

注意力模型 $h$

注意力模型为一个较深度的神经网络以指导边缘网络寻找边缘。FPN with ResNet-18。

$$\mathcal{L}(I,P,f,g,h)={\mathcal{L}}_{ce}(f(I),P)+\gamma |s(f(I)-g(I)\otimes h(I))|$$

Result