机器学习与支持向量机

第一层、了解SVM

1.0、什么是支持向量机SVM

    要明白什么是SVM，便得从分类说起。

    分类作为数据挖掘领域中一项非常重要的任务，它的目的是学会一个分类函数或分类模型(或者叫做分类器)，而支持向量机本身便是一种监督式学习的方法(至于具体什么是监督学习与非监督学习，请参见此系列Machine L&Data Mining第一篇)，它广泛的应用于统计分类以及回归分析中。

    支持向量机（SVM）是90年代中期发展起来的基于统计学习理论的一种机器学习方法，通过寻求结构化风险最小来提高学习机泛化能力，实现经验风险和置信范围的最小化，从而达到在统计样本量较少的情况下，亦能获得良好统计规律的目的。

    通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，即支持向量机的学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

1.1、线性分类

    OK，在讲SVM之前，咱们必须先弄清楚一个概念：线性分类器(也可以叫做感知机，这里的机表示的是一种算法，本文第三部分、证明SVM中会详细阐述)。

1.1.1、分类标准

    这里我们考虑的是一个两类的分类问题，数据点用 x 来表示，这是一个 n 维向量，w^T中的T代表转置，而类别用 y 来表示，可以取 1 或者 -1 ，分别代表两个不同的类。一个线性分类器的学习目标就是要在 n 维的数据空间中找到一个分类超平面，其方程可以表示为：

                                                           

    上面给出了线性分类的定义描述，但或许读者没有想过：为何用y取1 或者 -1来表示两个不同的类别呢？其实，这个1或-1的分类标准起源于logistic回归，为了完整和过渡的自然性，咱们就再来看看这个logistic回归。

1.1.2、1或-1分类标准的起源：logistic回归

    Logistic回归目的是从特征学习出一个0/1分类模型，而这个模型是将特性的线性组合作为自变量，由于自变量的取值范围是负无穷到正无穷。因此，使用logistic函数（或称作sigmoid函数）将自变量映射到(0,1)上，映射后的值被认为是属于y=1的概率。     形式化表示就是     假设函数

    其中x是n维特征向量，函数g就是logistic函数。     而 的图像是

    可以看到，将无穷映射到了(0,1)。     而假设函数就是特征属于y=1的概率。

     当我们要判别一个新来的特征属于哪个类时，只需求，若大于0.5就是y=1的类，反之属于y=0类。

1.4、最大间隔分类器Maximum Margin Classifier的定义

    于此，我们已经很明显的看出，函数间隔functional margin 和 几何间隔geometrical margin 相差一个的缩放因子。按照我们前面的分析，对一个数据点进行分类，当它的 margin 越大的时候，分类的 confidence 越大。对于一个包含 n 个点的数据集，我们可以很自然地定义它的 margin 为所有这 n 个点的 margin 值中最小的那个。于是，为了使得分类的 confidence 高，我们希望所选择的超平面hyper plane 能够最大化这个 margin 值。

    通过上节，我们已经知道：

1、functional margin 明显是不太适合用来最大化的一个量，因为在 hyper plane 固定以后，我们可以等比例地缩放 w 的长度和 b 的值，这样可以使得的值任意大，亦即 functional margin可以在 hyper plane 保持不变的情况下被取得任意大，

2、而 geometrical margin 则没有这个问题，因为除上了这个分母，所以缩放 w 和 b 的时候的值是不会改变的，它只随着 hyper plane 的变动而变动，因此，这是更加合适的一个 margin 。

    通过最大化 margin ，我们使得该分类器对数据进行分类时具有了最大的 confidence，从而设计决策最优分类超平面。

1.5、到底什么是Support Vector

    上节，我们介绍了Maximum Margin Classifier，但并没有具体阐述到底什么是Support Vector，本节，咱们来重点阐述这个概念。咱们不妨先来回忆一下上节1.4节最后一张图：

    可以看到两个支撑着中间的 gap 的超平面，它们到中间的纯红线separating hyper plane 的距离相等，即我们所能得到的最大的 geometrical margin，而“支撑”这两个超平面的必定会有一些点，而这些“支撑”的点便叫做支持向量Support Vector。

   或亦可看下来自此PPT中的一张图，Support Vector便是那蓝色虚线和粉红色虚线上的点：

    很显然，由于这些 supporting vector 刚好在边界上，所以它们满足（还记得我们把 functional margin 定为 1 了吗？上节中：“处于方便推导和优化的目的，我们可以令=1”），而对于所有不是支持向量的点，也就是在“阵地后方”的点，则显然有。当然，除了从几何直观上之外，支持向量的概念也可以从下文优化过程的推导中得到。

    OK，到此为止，算是了解到了SVM的第一层，对于那些只关心怎么用SVM的朋友便已足够，不必再更进一层深究其更深的原理。

2.2、核函数Kernel

2.2.1、特征空间的隐式映射：核函数

    咱们首先给出核函数的来头：

• 在上文中，我们已经了解到了SVM处理线性可分的情况，而对于非线性的情况，SVM 的处理方法是选择一个核函数 κ(⋅,⋅) ，通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。由于核函数的优良品质，这样的非线性扩展在计算量上并没有比原来复杂多少，这一点是非常难得的。当然，这要归功于核方法——除了 SVM 之外，任何将计算表示为数据点的内积的方法，都可以使用核方法进行非线性扩展。

    也就是说，Minsky和Papert早就在20世纪60年代就已经明确指出线性学习器计算能力有限。为什么呢？因为总体上来讲，现实世界复杂的应用需要有比线性函数更富有表达能力的假设空间，也就是说，目标概念通常不能由给定属性的简单线性函数组合产生，而是应该一般地寻找待研究数据的更为一般化的抽象特征。

    而下文我们将具体介绍的核函数则提供了此种问题的解决途径，从下文你将看到，核函数通过把数据映射到高维空间来增加第一节所述的线性学习器的能力，使得线性学习器对偶空间的表达方式让分类操作更具灵活性和可操作性。因为训练样例一般是不会独立出现的，它们总是以成对样例的内积形式出现，而用对偶形式表示学习器的优势在为在该表示中可调参数的个数不依赖输入属性的个数，通过使用恰当的核函数来替代内积，可以隐式得将非线性的训练数据映射到高维空间，而不增加可调参数的个数(当然，前提是核函数能够计算对应着两个输入特征向量的内积)。

    1、简而言之：在线性不可分的情况下，支持向量机通过某种事先选择的非线性映射(核函数)将输入变量映射到一个高维特征空间，在这个空间中构造最优分类超平面。我们使用SVM进行数据集分类工作的过程首先是同预先选定的一些非线性映射将输入空间映射到高维特征空间(下图很清晰的表达了通过映射到高维特征空间，而把平面上本身不好分的非线性数据分了开来)：

    使得在高维属性空间中有可能最训练数据实现超平面的分割，避免了在原输入空间中进行非线性曲面分割计算。SVM数据集形成的分类函数具有这样的性质：它是一组以支持向量为参数的非线性函数的线性组合，因此分类函数的表达式仅和支持向量的数量有关，而独立于空间的维度，在处理高维输入空间的分类时，这种方法尤其有效，其工作原理如下图所示：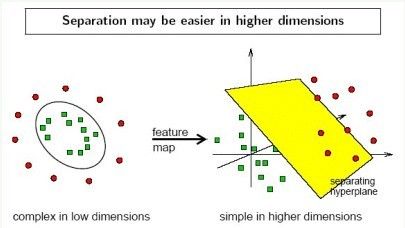

   

2.2.3、几个核函数

    通常人们会从一些常用的核函数中选择（根据问题和数据的不同，选择不同的参数，实际上就是得到了不同的核函数），例如：

• 多项式核，显然刚才我们举的例子是这里多项式核的一个特例（R = 1，d = 2）。虽然比较麻烦，而且没有必要，不过这个核所对应的映射实际上是可以写出来的，该空间的维度是，其中  是原始空间的维度。
• 高斯核，这个核就是最开始提到过的会将原始空间映射为无穷维空间的那个家伙。不过，如果选得很大的话，高次特征上的权重实际上衰减得非常快，所以实际上（数值上近似一下）相当于一个低维的子空间；反过来，如果选得很小，则可以将任意的数据映射为线性可分——当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。不过，总的来说，通过调控参数，高斯核实际上具有相当高的灵活性，也是使用最广泛的核函数之一。下图所示的例子便是把低维线性不可分的数据通过高斯核函数映射到了高维空间：
• 线性核，这实际上就是原始空间中的内积。这个核存在的主要目的是使得“映射后空间中的问题”和“映射前空间中的问题”两者在形式上统一起来了(意思是说，咱们有的时候，写代码，或写公式的时候，只要写个模板或通用表达式，然后再代入不同的核，便可以了，于此，便在形式上统一了起来，不用再分别写一个线性的，和一个非线性的)。

2.2.4、核函数的本质

         上面说了这么一大堆，读者可能还是没明白核函数到底是个什么东西？我再简要概括下，即以下三点：

1. 实际中，我们会经常遇到线性不可分的样例，此时，我们的常用做法是把样例特征映射到高维空间中去(如上文2.2节最开始的那幅图所示，映射到高维空间后，相关特征便被分开了，也就达到了分类的目的)；
2. 但进一步，如果凡是遇到线性不可分的样例，一律映射到高维空间，那么这个维度大小是会高到可怕的(如上文中19维乃至无穷维的例子)。那咋办呢？
3. 此时，核函数就隆重登场了，核函数的价值在于它虽然也是讲特征进行从低维到高维的转换，但核函数绝就绝在它事先在低维上进行计算，而将实质上的分类效果表现在了高维上，也就如上文所说的避免了直接在高维空间中的复杂计算。

.3、使用松弛变量处理 outliers 方法

    在本文第一节最开始讨论支持向量机的时候，我们就假定，数据是线性可分的，亦即我们可以找到一个可行的超平面将数据完全分开。后来为了处理非线性数据，在上文2.2节使用 Kernel 方法对原来的线性 SVM 进行了推广，使得非线性的的情况也能处理。虽然通过映射  将原始数据映射到高维空间之后，能够线性分隔的概率大大增加，但是对于某些情况还是很难处理。

    例如可能并不是因为数据本身是非线性结构的，而只是因为数据有噪音。对于这种偏离正常位置很远的数据点，我们称之为 outlier ，在我们原来的 SVM 模型里，outlier 的存在有可能造成很大的影响，因为超平面本身就是只有少数几个 support vector 组成的，如果这些 support vector 里又存在 outlier 的话，其影响就很大了。例如下图：

    用黑圈圈起来的那个蓝点是一个 outlier ，它偏离了自己原本所应该在的那个半空间，如果直接忽略掉它的话，原来的分隔超平面还是挺好的，但是由于这个 outlier 的出现，导致分隔超平面不得不被挤歪了，变成途中黑色虚线所示（这只是一个示意图，并没有严格计算精确坐标），同时 margin 也相应变小了。当然，更严重的情况是，如果这个 outlier 再往右上移动一些距离的话，我们将无法构造出能将数据分开的超平面来。

    为了处理这种情况，SVM 允许数据点在一定程度上偏离一下超平面。例如上图中，黑色实线所对应的距离，就是该 outlier 偏离的距离，如果把它移动回来，就刚好落在原来的超平面上，而不会使得超平面发生变形了

一、导入sklearn算法包

　　Scikit-Learn库已经实现了所有基本机器学习的算法，具体使用详见官方文档说明：http://scikit-learn.org/stable/auto_examples/index.html#support-vector-machines。

　　skleran中集成了许多算法，其导入包的方式如下所示，

　　逻辑回归：from sklearn.linear_model import LogisticRegression

      朴素贝叶斯：from sklearn.naive_bayes import GaussianNB

 　　K-近邻：from sklearn.neighbors import KNeighborsClassifier

 　　决策树：from sklearn.tree import DecisionTreeClassifier

 　　支持向量机：from sklearn import svm

 二、sklearn中svc的使用

（1）使用numpy中的loadtxt读入数据文件

　　loadtxt()的使用方法：

　　

　　fname:文件路径。eg：C:/Dataset/iris.txt。

　　dtype：数据类型。eg：float、str等。

　　delimiter：分隔符。eg：‘，’。

　　converters：将数据列与转换函数进行映射的字典。eg：{1:fun}，含义是将第2列对应转换函数进行转换。

　　usecols：选取数据的列。

　　以Iris兰花数据集为例子：

　　由于从UCI数据库中下载的Iris原始数据集的样子是这样的，前四列为特征列，第五列为类别列，分别有三种类别Iris-setosa， Iris-versicolor， Iris-virginica。　　　

　　

　　当使用numpy中的loadtxt函数导入该数据集时，假设数据类型dtype为浮点型，但是很明显第五列的数据类型并不是浮点型。

　　因此我们要额外做一个工作，即通过loadtxt()函数中的converters参数将第五列通过转换函数映射成浮点类型的数据。

　　首先，我们要写出一个转换函数：

def  iris_type(s):
    it  =  { 'Iris-setosa' :  0 ,  'Iris-versicolor' :  1 ,  'Iris-virginica' :  2 }
    return  it[s]

　　接下来读入数据，converters={4: iris_type}中“4”指的是第5列：

path  =  u 'D:/f盘/python/学习/iris.data'   # 数据文件路径
data  =  np.loadtxt(path, dtype = float , delimiter = ',' , converters = { 4 : iris_type})

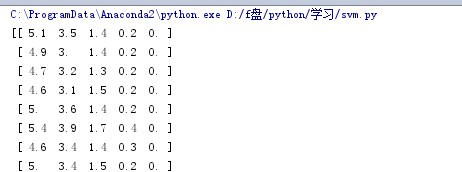
　　读入结果：

　　

（2）将Iris分为训练集与测试集

x, y  =  np.split(data, ( 4 ,), axis = 1 )
x  =  x[:, : 2 ]
x_train, x_test, y_train, y_test  =  train_test_split(x, y, random_state = 1 , train_size = 0.6 )

　　1. split(数据，分割位置，轴=1（水平分割） or 0（垂直分割）)。

　　2. x = x[:, :2]是为方便后期画图更直观，故只取了前两列特征值向量训练。

　　3. sklearn.model_selection.train_test_split随机划分训练集与测试集。train_test_split(train_data,train_target,test_size=数字, random_state=0)

　　参数解释：

　　train_data：所要划分的样本特征集

　　train_target：所要划分的样本结果

　　test_size：样本占比，如果是整数的话就是样本的数量

　　random_state：是随机数的种子。

　　随机数种子：其实就是该组随机数的编号，在需要重复试验的时候，保证得到一组一样的随机数。比如你每次都填1，其他参数一样的情况下你得到的随机数组是一样的。但填0或不填，每次都会不一样。随机数的产生取决于种子，随机数和种子之间的关系遵从以下两个规则：种子不同，产生不同的随机数；种子相同，即使实例不同也产生相同的随机数。

（3）训练svm分类器

# clf = svm.SVC(C=0.1, kernel='linear', decision_function_shape='ovr')
    clf  =  svm.SVC(C = 0.8 , kernel = 'rbf' , gamma = 20 , decision_function_shape = 'ovr' )
    clf.fit(x_train, y_train.ravel())

 　　kernel='linear'时，为线性核，C越大分类效果越好，但有可能会过拟合（defaul C=1）。

　　 kernel='rbf'时（default），为高斯核，gamma值越小，分类界面越连续；gamma值越大，分类界面越“散”，分类效果越好，但有可能会过拟合。

　　decision_function_shape='ovr'时，为one v rest，即一个类别与其他类别进行划分，

　　decision_function_shape='ovo'时，为one v one，即将类别两两之间进行划分，用二分类的方法模拟多分类的结果。

（4）计算svc分类器的准确率

print  clf.score(x_train, y_train)   # 精度
y_hat  =  clf.predict(x_train)
show_accuracy(y_hat, y_train,  '训练集' )
print  clf.score(x_test, y_test)
y_hat  =  clf.predict(x_test)
show_accuracy(y_hat, y_test,  '测试集' )

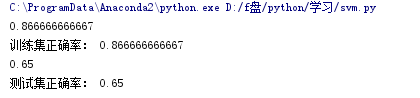
 结果为：

　　如果想查看决策函数，可以通过decision_function()实现

print  'decision_function:\n' , clf.decision_function(x_train)
print  '\npredict:\n' , clf.predict(x_train)

 结果为：

　　decision_function中每一列的值代表距离各类别的距离。

（5）绘制图像

　　1.确定坐标轴范围，x，y轴分别表示两个特征

x1_min, x1_max  =  x[:,  0 ]. min (), x[:,  0 ]. max ()   # 第0列的范围
x2_min, x2_max  =  x[:,  1 ]. min (), x[:,  1 ]. max ()   # 第1列的范围
x1, x2  =  np.mgrid[x1_min:x1_max: 200j , x2_min:x2_max: 200j ]   # 生成网格采样点
grid_test  =  np.stack((x1.flat, x2.flat), axis = 1 )   # 测试点
# print 'grid_test = \n', grid_testgrid_hat = clf.predict(grid_test)       # 预测分类值grid_hat = grid_hat.reshape(x1.shape)  # 使之与输入的形状相同

 　　这里用到了mgrid()函数，该函数的作用这里简单介绍一下：

　　 假设假设目标函数F（x，y）=x+y。x轴范围1~3，y轴范围4~6，当绘制图像时主要分四步进行：

　　【step1：x扩展】(朝右扩展)：

       [1 1 1]

　　 [2 2 2]

　　 [3 3 3]

　　【step2：y扩展】(朝下扩展)：

　　 [4 5 6]

　　 [4 5 6]

　　 [4 5 6]

　　【step3：定位（xi，yi）】：

　　 [(1,4) (1,5) (1,6)]

　　 [(2,4) (2,5) (2,6)]

　　 [(3,4) (3,5) (3,6)]

　　【step4：将（xi，yi）代入F(x,y)=x+y】

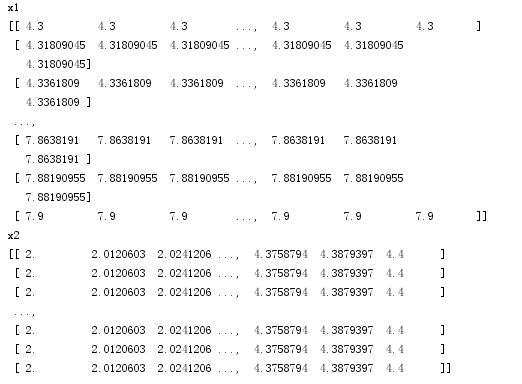
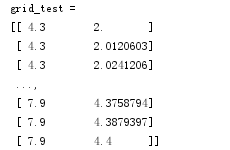
　　因此这里x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]后的结果为：

　　

　　再通过stack()函数，axis=1，生成测试点

　　

　　2.指定默认字体

mpl.rcParams[ 'font.sans-serif' ]  =  [u 'SimHei' ]
mpl.rcParams[ 'axes.unicode_minus' ]  =  False

　　3.绘制

cm_light  =  mpl.colors.ListedColormap([ '#A0FFA0' ,  '#FFA0A0' ,  '#A0A0FF' ])
cm_dark  =  mpl.colors.ListedColormap([ 'g' ,  'r' ,  'b' ])
plt.pcolormesh(x1, x2, grid_hat, cmap = cm_light)
plt.scatter(x[:,  0 ], x[:,  1 ], c = y, edgecolors = 'k' , s = 50 , cmap = cm_dark)   # 样本
plt.scatter(x_test[:,  0 ], x_test[:,  1 ], s = 120 , facecolors = 'none' , zorder = 10 )   # 圈中测试集样本
plt.xlabel(u '花萼长度' , fontsize = 13 )
plt.ylabel(u '花萼宽度' , fontsize = 13 )
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.title(u '鸢尾花SVM二特征分类' , fontsize = 15 )
# plt.grid()
plt.show()

 　　pcolormesh(x,y,z,cmap)这里参数代入x1，x2，grid_hat，cmap=cm_light绘制的是背景。

　　 scatter中edgecolors是指描绘点的边缘色彩，s指描绘点的大小，cmap指点的颜色。

　　 xlim指图的边界。

最终结果为：

 

完整代码

# -*- coding:utf-8 -*-
# -*- coding:utf-8 -*-
from  sklearn  import  svm
import  numpy as np
import  matplotlib.pyplot as plt
import  matplotlib as mpl
from  matplotlib  import  colors
from  sklearn.model_selection  import  train_test_split
def  iris_type(s):
    it  =  { 'Iris-setosa' :  0 ,  'Iris-versicolor' :  1 ,  'Iris-virginica' :  2 }
    return  it[s]
def  show_accuracy(y_hat, y_test, param):
    pass

path  =  'F:\\Test\\iris.data'  # 数据文件路径
data  =  np.loadtxt(path, dtype = float , delimiter = ',' , converters = { 4 : iris_type})

x, y  =  np.split(data, ( 4 ,), axis = 1 )
x  =  x[:, : 2 ]
x_train, x_test, y_train, y_test  =  train_test_split(x, y, random_state = 1 , train_size = 0.6 )

# clf = svm.SVC(C=0.1, kernel='linear', decision_function_shape='ovr')
clf  =  svm.SVC(C = 0.8 , kernel = 'rbf' , gamma = 20 , decision_function_shape = 'ovr' )
clf.fit(x_train, y_train.ravel())

print  clf.score(x_train, y_train)   # 精度
y_hat  =  clf.predict(x_train)
show_accuracy(y_hat, y_train,  '训练集' )
print  clf.score(x_test, y_test)
y_hat  =  clf.predict(x_test)
show_accuracy(y_hat, y_test,  '测试集' )

print  'decision_function:\n' , clf.decision_function(x_train)
print  '\npredict:\n' , clf.predict(x_train)

x1_min, x1_max  =  x[:,  0 ]. min (), x[:,  0 ]. max ()   # 第0列的范围
x2_min, x2_max  =  x[:,  1 ]. min (), x[:,  1 ]. max ()   # 第1列的范围
x1, x2  =  np.mgrid[x1_min:x1_max: 200j , x2_min:x2_max: 200j ]   # 生成网格采样点
grid_test  =  np.stack((x1.flat, x2.flat), axis = 1 )   # 测试点


mpl.rcParams[ 'font.sans-serif' ]  =  [u 'SimHei' ]
mpl.rcParams[ 'axes.unicode_minus' ]  =  False

cm_light  =  mpl.colors.ListedColormap([ '#A0FFA0' ,  '#FFA0A0' ,  '#A0A0FF' ])
cm_dark  =  mpl.colors.ListedColormap([ 'g' ,  'r' ,  'b' ])

# print 'grid_test = \n', grid_test
grid_hat  =  clf.predict(grid_test)        # 预测分类值
grid_hat  =  grid_hat.reshape(x1.shape)   # 使之与输入的形状相同

alpha  =  0.5
plt.pcolormesh(x1, x2, grid_hat, cmap = cm_light)      # 预测值的显示
# plt.scatter(x[:, 0], x[:, 1], c=y, edgecolors='k', s=50, cmap=cm_dark)  # 样本
plt.plot(x[:,  0 ], x[:,  1 ],  'o' , alpha = alpha, color = 'blue' , markeredgecolor = 'k' )
plt.scatter(x_test[:,  0 ], x_test[:,  1 ], s = 120 , facecolors = 'none' , zorder = 10 )   # 圈中测试集样本
plt.xlabel(u '花萼长度' , fontsize = 13 )
plt.ylabel(u '花萼宽度' , fontsize = 13 )
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.title(u '鸢尾花SVM二特征分类' , fontsize = 15 )
# plt.grid()
plt.show()