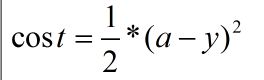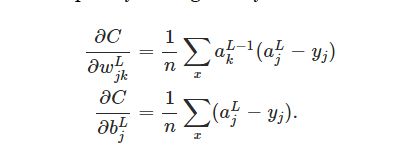Micheal Nielsen's神经网络学习之二

依然是跟着Michael Nielsen的神经网络学习，基于前一篇的学习，已经大概明白了神经网络的基本结构和BP算法，也能通过神经网络训练数字识别功能，之后我试验了一下使用神经网络训练之前的文本分类，只是简单的使用了词频来作为词向量处理过程，没有任何的其他调参过程，对于八分类，其正确率到了84%，相比于之前各种调参才能勉强达到72%的SVM分类方法而言，神经网络有无可比拟的简单和高正确率。好了，安利了这么久的神经网络，现在是时候回归正题了

这一篇以及后面的文章涉及到神经网络的调优问题，有人会说“看，神经网络也需要调参”，其实我想表达的是神经网络在不调参的时候准确度已经非常好了，调参只是为了更上一层楼，而且神经网络调参绝对比支持向量机(SVM)简单的多，这是我喜欢神经网络的原因。

神经网络调参包括三个方面：

**1. 损失函数的选取Loss Function
2. 正则化
3. 初始参数w和b的选取**

本文主要是就第一个方面来进行优化，也就是选取新的损失函数来加快学习过程。

简要回忆一下前一篇文章Michael Nielsen’s神经网络学习之一上面的损失函数，也就是二次损失函数：quadratic cost 。其基本形式是：

这个损失函数有什么问题呢，其实二次损失函数有很多的有点，比如容易求导，也能基本表征”损失“这一词的意思。现在让我们看下对于一个具体的神经元，这个损失函数的表现过程。

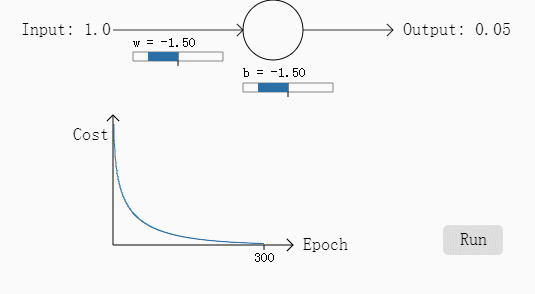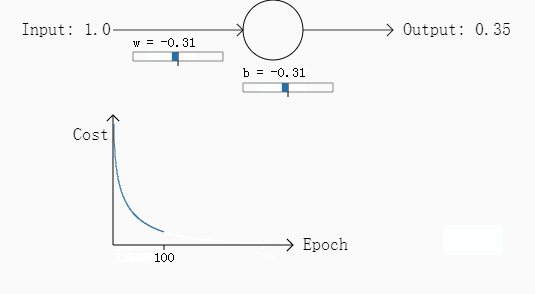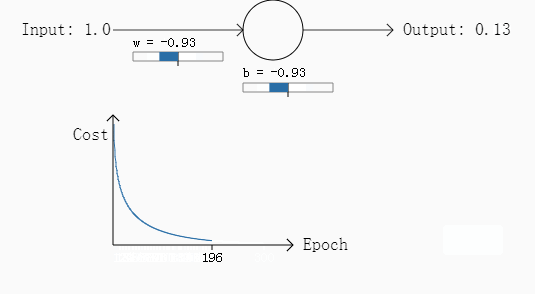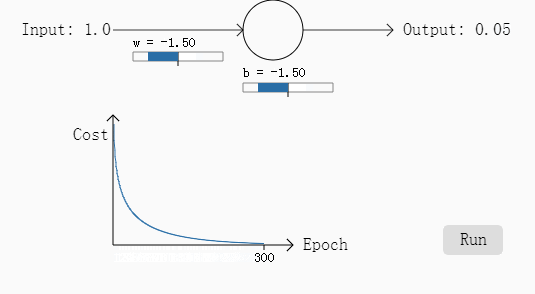
首先对于下图的单个神经元，我们假设初始化的权重w=0.6,以及偏移量b=0.9以及步长n=0.15,然后我们假设这个神经元的应该输出的结果是0.0，按照以往的神经元计算方法，我们计算出来的结果是0.82，初始的误差较大，然后我们观察在这个神经元使用梯度下降法的过程中的参数变化过程：

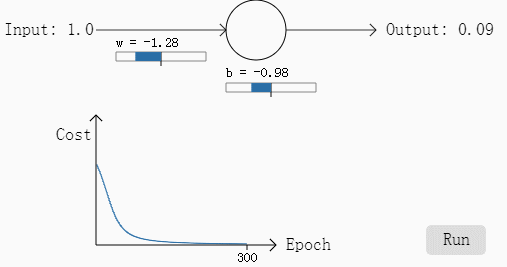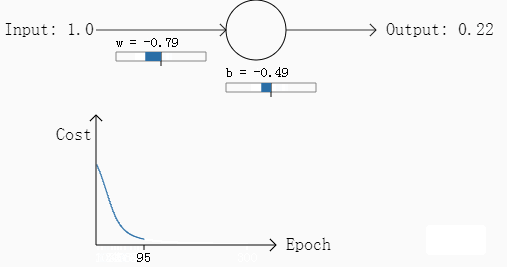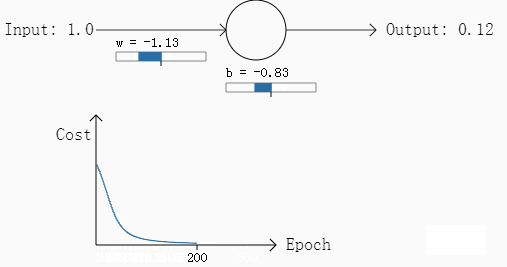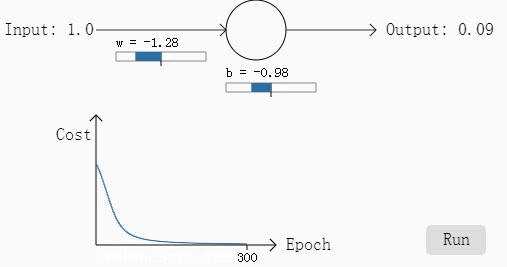
从图中可以看到结果还是很给力的，300次迭代之后结果为0.09，和结果相差也不算大，恩，这是其中一个例子。

我们再来看另一个例子，同样使用二次损失函数，但是我们把最初的权重w和b都设计为2，步长为0.15不变，应该输出的结果为0也不变，按照这个参数第一次计算的结果是0.98，相差比第一次大，同样我们看一下其参数在梯度下降过程中的变化过程：

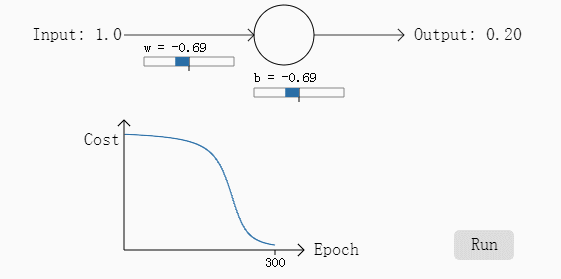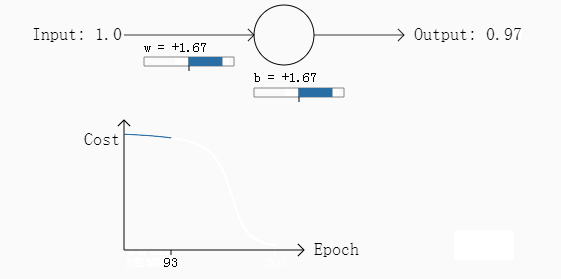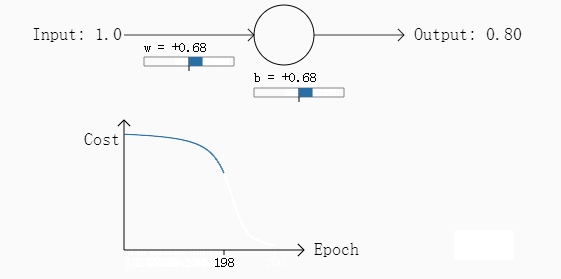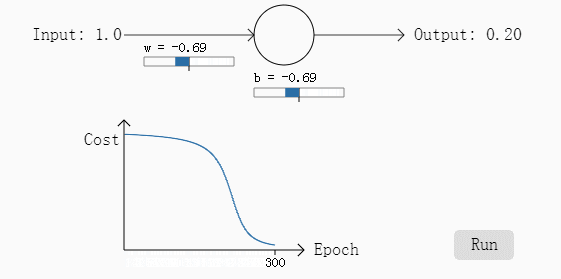
经过30次迭代之后，其输出的结果是0.2，误差较第一次变大了不少。

通过这两次的例子，我们可以发现什么，在第二个例子中，其初始参数偏差非常发，因此初始的误差非常大，但是从其变化图可以看出，其学习过程相当缓慢（曲线比较平滑），从人的角度考虑，如果给定初始的参数，一个人发现这个参数的偏差非常大，通常这个人会将参数调整的幅度变大而不是变小，但是从第二个例子来看，二次损失函数恰恰相反，这一个特性无疑降低了学习的速度。

回顾前面的神经网络，我们在最开始选取w和b的时候是使用随机的数产生，在二次损失函数的情况下，这就产生了严重的问题，如果我们随机生成的数稍微正常一点，如上面的例一，我们可以收敛的快一点，但是如果我们生成的数开始偏差就非常大，这非常容易导致最后的收敛过程过度缓慢的问题。

现在我们从数学的角度，想象为什么二次损失函数会在参数误差很大的情况下学习速度反而放缓。
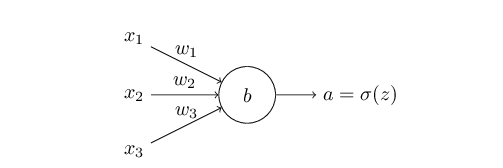
为了简要起见，我们以单个的神经元为例。
首先损失函数：

对应的其求导方法：

因为使用了sigmoid函数，那么a的取值在（0,1）之间，由上面的求导公式可以看出，当a和y相差很大的情况下，该求导值反而低，也就是说这个值得输出和误差值的大小并不是呈直接线性相关的，这也就是为什么二次损失函数容易出现学习过慢的问题

鉴于二次损失函数的上面所说的确定，这就引入了”互熵“损失函数（corss-entropy cost function），或者叫交叉熵。
还是以单个的神经元为例：

我们来看一下互熵的表示形式：

其实这个和一般的熵的形式也没什么区别，下面来说一下为什么”互熵“能够起到损失函数的作用。总结起来有一下几点好处：

1. 其值为正
2. 和输出数据之间有依赖关系

3. 对w和b求分导的结果和误差值呈正相关

   下面具体来说说具体的方面。
   对于第一点：这是显然的

对于第二点：我们可以看到，假如应该输出的结果是1的话，当我们通过神经元得到的输出也接近为1的时候其值为0，当我们通过神经元得到的输出为0的时候，其值是1，也就是基本上满足损失函数所要求的功能

对于第三点：我们容易得到：

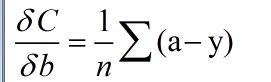
其中a为神经元的输出值
由上面的求导公式很容易得到结论：当误差值较大的时候，w和b的下降梯度也会变大，这和我们想要的功能是一样的。
现在来测试一下使用互熵作为损失函数的效果，和文章开篇测试的方法一样，只是对于单个神经元的测试：

例一：初始权重w为0.6，偏移b=0.9，需要的输出是0，步长为0.15.

例二：w和b都为2，需要输出是0，步长为0.15

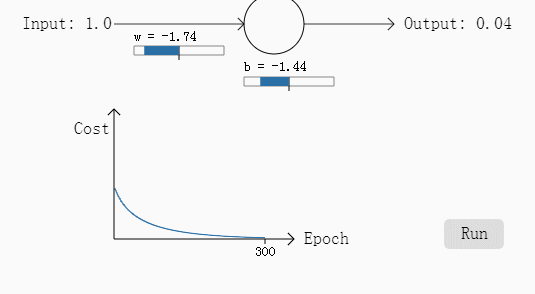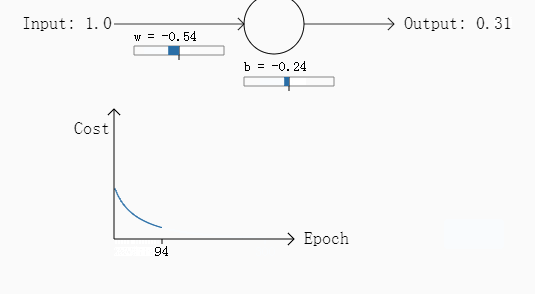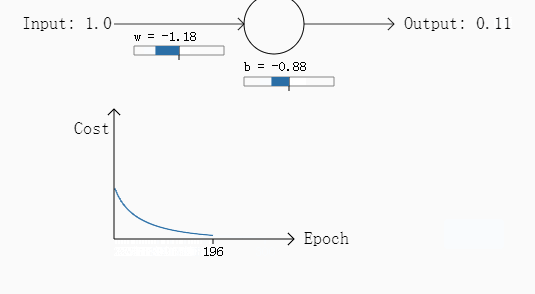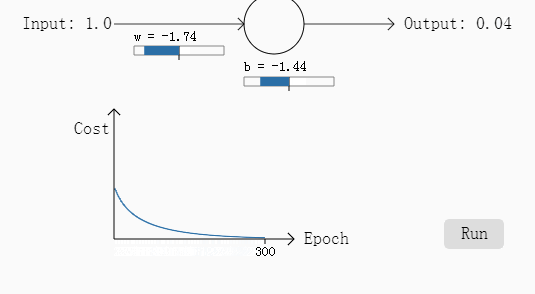
可以看出如果误差越大，其下降的梯度也就越大，也就是说学习过程加快了，达到了我们要的效果。

拓展到多层多个神经元，其求导方式是一样的，只不过多了一些参数罢了

在使用了互熵作为损失函数之后，之前的神经网络代码就需要改变了，不过只是需要改变一下在BP步骤里面的求导值即可

delta = (self.cost).delta(zs[-1], activations[-1], y) #(1)
nabla_b[-1] = delta  #(2)
nabla_w[-1] = np.dot(delta, activations[-2].transpose()) #(3)

其中在第一步中

delta计算值为：activations[-1]-y
这个和我们上面的求导结果是一样的。

END!

参考文献：《Improving the way neural networks learn》 Michael Nielsen神经网络与深度学习