李航《统计学习方法》第二版-第3章 k近邻法 浅见

3.0 k近邻简单介绍

k近邻暂时讨论分类方法，可以简单理解为我要去个地方，我找周围k个最近的人问问该走哪条路(对应类别)，告诉我最多走的那条路就是我要走的路。你选k个人，选离你多远的人，选择哪条路对应着k值选择，距离度量和分类决策规则，是k近邻法的三个基本要素。实际上这3个要素定了之后，就对样本的特征空间进行了划分，也就可以分类了。

3.1 k近邻算法

算法就是上面说到的分类决策规则，选告诉你最多的那条路，就是统计所有k个人告诉你的路，哪条路的数量最多，就认为是哪条路。

算法步骤：

输入：训练集$$T=(x_1,y_1),(x_2,y_2),...,(x_N,y_N)$$
其中$x_i\in X=R^n$为样本的特征向量$y_i\in Y=\{c_1,c_2,...,c_K\}$为样本的类别，$i=1,2,..,N$。

输出：y的类别
1.根据给定距离度量，找出距离x个最近的k个样本点，涵盖k个点的x的邻域即做$N_k(x)$.
2.在$N_k(x)$中选择类别数量最多的类别作为y的类别：
$$y=arg\underset{c_j}{\max }\sum _{x_i\in N_k(x)}I(y_i=c_i),i=1,2,...,K$$
$I$为指示函数，即$y_i=c_i$时$I=1$，否则$I=0$.
可见k近邻没有跟其他算法一样的学习过程，只是衡量周围的类别多少。
那张图来做说明，绿色的点是新来的样本，如果他根据最近3个点，而且距离度量是实线圆内的话，会发现有2个红色，一个蓝色，那红色的类别多，所以新来的应该是红色。但是如果把点扩大为5个，距离度量扩大到虚线圆内，居然发现蓝色3个比红色2个多，那就变成是蓝色的类别了，可见具体什么类别跟k值和距离度量关系很大啊：

3.2 k近邻模型

3.2.1 模型

在k近邻中，如果k值，距离度量确定，分类决策规则确定，那新的实例的类别就确定了，这相当于把特征空间进行了划分，确定了每个点的类别。

3.2.2 距离度量

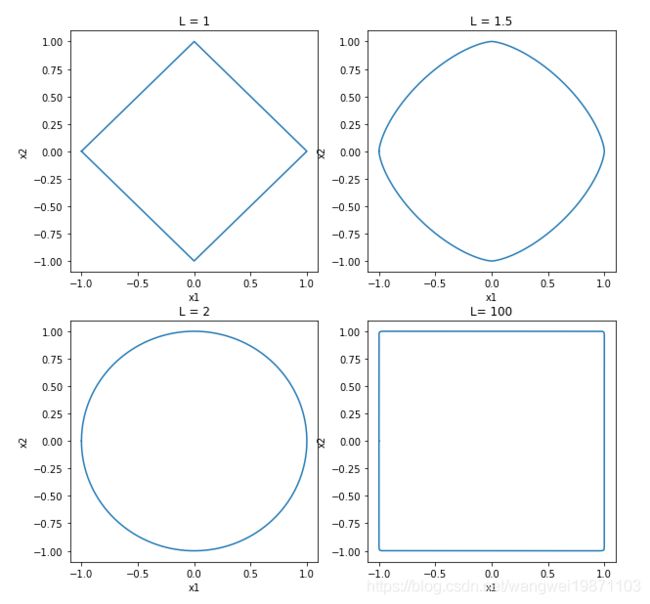
其实距离度量，就是反应出两个样本之间的相似程度，如果距离很小，就说明很相近，如果距离0就说明一样啦。一般的距离有欧氏距离，曼哈顿距离，更一般的可以归结为$L_p距离:
$$L_p(x_i,x_j)=(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^p{)}^{\frac{1}{p}}$$

其中$p \geq1 $ 。
$l表示第l维特征 $。
$x_i,x_j$表示n维实数向量 。

当$p=2 $时就是欧氏距离：
$$L_2(x_i,x_j)=\sqrt{\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^2)}$$

当$p=1 $时就是曼哈顿距离：
$$L_2(x_i,x_j)=\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}|$$

当$p=\infty $时就是各个坐标之间的距离的最大值：
$$L_{\infty }(x_i,x_j)=\underset{l}{\max }|x_i^{(l)}-x_j^{(l)}|$$

用我上次画的范数图表示下，是同一个意思：

3.2.3 k值选择

如果k很小，那训练集的误差会小，但是测试误差会大，就是过拟合了，简单可以理解为你参考的样本太少了，如果那个点刚好是噪声，那就错啦，所以你只看到了一部分，或许周围大部分都是其他类别呢。

如果k很大，最大就是整个训练集，这样训练误差会很大，每次都是同一个类别，因为每次都找数量最大的。这样就是过于简单了，可能欠拟合。

所以选k很重要，一般是下去比较小的值，然后采用交叉验证方法来选取最优的k值。

3.2.4 分类决策规则

这个就是算法，前面已经介绍过了，就不多说了，重复写公式没啥意思。只是引出了一个误分类率的概念，其实就是错分类数量除以k。

3.3 kd树

这个要写起来比较麻烦，而且本人能力有限，所以还是写个思路，如果按一般的方法就是直接计算每个点距离，这样计算量很大，所以我们可以用类似分治法的思想，先把训练集的特征空间分一下，用类似平衡二叉树的思想分，然后就可以减少计算量了，具体可以百度下。

总结

介绍了k近邻的基本思想和算法，具体实践还是需要有优化，不然计算量很大，优化的思想就是平衡二叉树和分治法的思想，降低计算量。

好了，今天就到这里了，希望对学习理解有帮助，大神看见勿喷，仅为自己的学习理解，能力有限，请多包涵，部分图片来自网络,侵删。