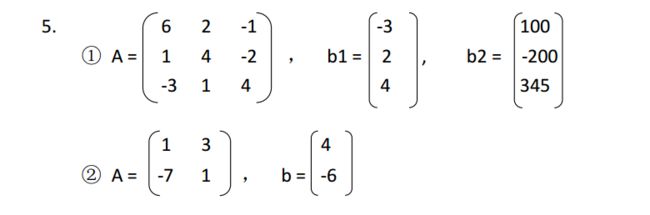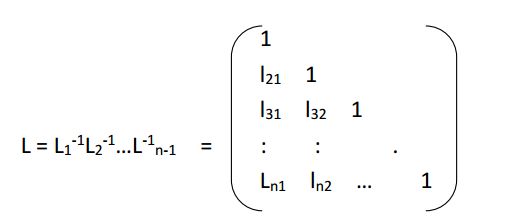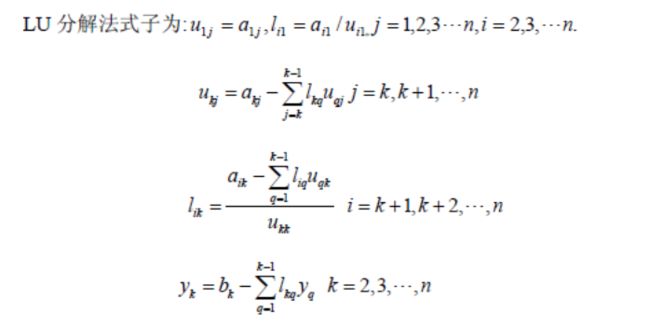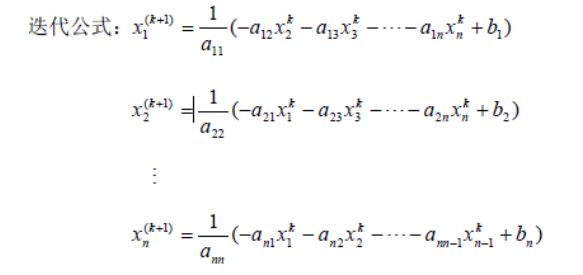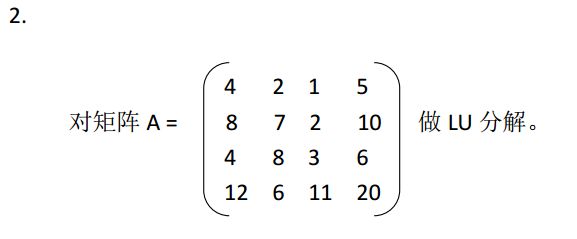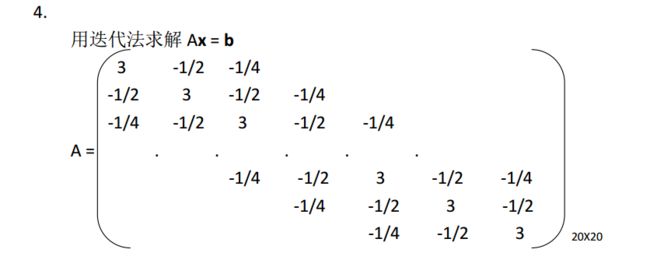数值实验报告
----------------------个人作业,如果有后辈的作业习题一致,可以参考学习,一起交流,请勿直接copy
一、 实验目的
- 了解并分析LU分解法的优点;
- 追赶法的应用与其与LU分解法的对比;
- 认识迭代法收敛的含义以及迭代法初值和方程组系数矩阵性质对收敛速度的影响。
二、 实验题目
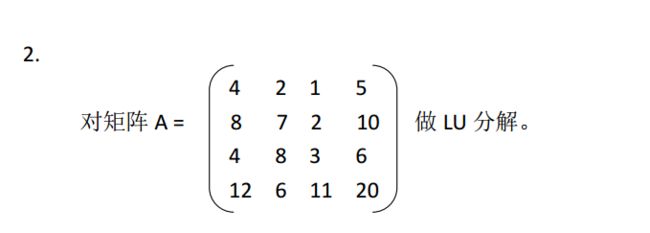
三、 实验原理
l LU分解:
- ·如果对A(0)x = b(0)施行第一次消元后化为A(1)x = b(1),则存在L1,使得
L1A(0)=A(1),L1b(0)= b(1)
一般地,进行k次消元化后为A(k)x = b(k), 则有
LkA(k-1)=A(k),Lkb(k-1)= b(k)
重复这一过程,最后得到
Ln-1…L2L1A(0) = A(n-1)
Ln-1…L2L1b(0) = b(n-1)
将上三角形矩阵A(n-1)记为U,则 A=LU ,其中
为下三角矩阵。利用高斯消元法实质上产生了一个将A分解为两个三角形矩阵相乘的因式分解,称为A的三角形分解或LU分解。
·矩阵分解不一定采用高斯消元法,以下为直接计算的计算公式:
把增广矩阵A 采用LU 分解格式,即可得到与原方程同解的方
程组。即 Ax=b ⇒ LUx = b ⇒ Ux= L−1b,由U为上三角矩阵,而后回代即可求出原方程的解。
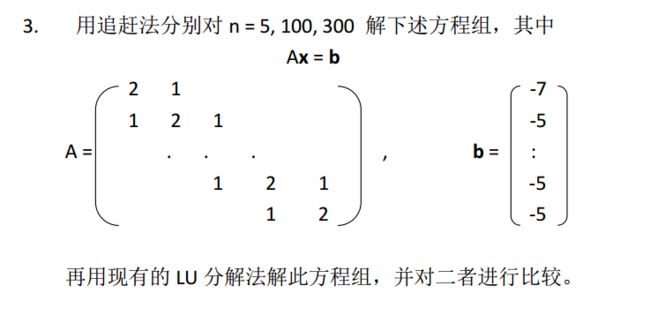
l 追赶法:
求解Ax = b 等价于解两个二对角线方程组
Ly = b
Ux =y
自上而下解方程组Ly = b 形象地被称为“追”。
y1 = b1/l11
yi =bi-lii-1yi-1/lii, i = 2, 3, … ,n
自下而上解方程组Ux = y 形象地被称为“赶”。
xn=yn
xi =yi-uii+1xi+1, i = n-1, … ,2,1
习惯上,上述求解方法称为“追赶法”。
l 迭代法:
- ·雅克比迭代雅克比迭代法基本思想与迭代法相同是一种逐次逼近的方法。首先给定一个较粗糙的初值,然后采用迭代公式,进行多次迭代,直到满足所要求的精度为止。
·高斯-赛德尔迭代法基本思想基本与雅克比迭代法相同
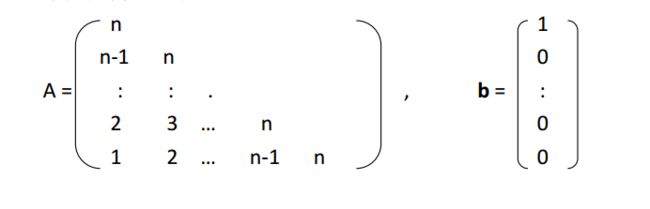
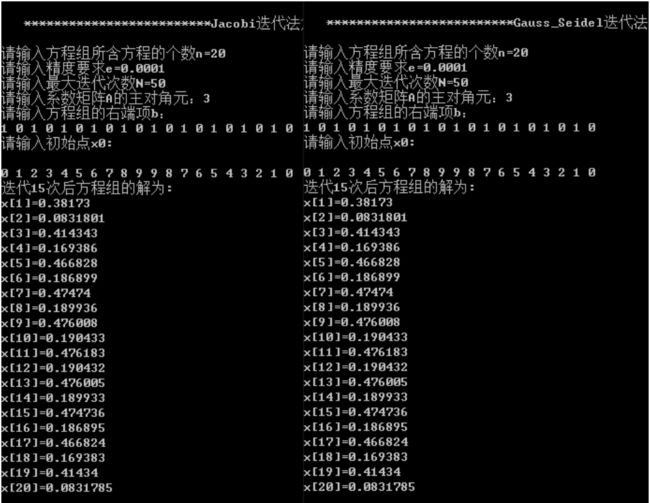
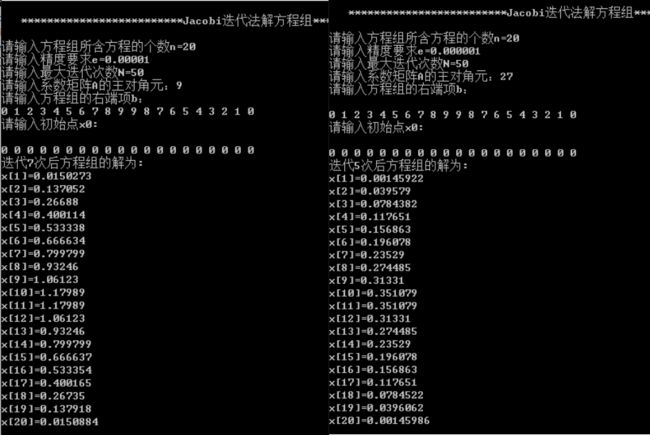
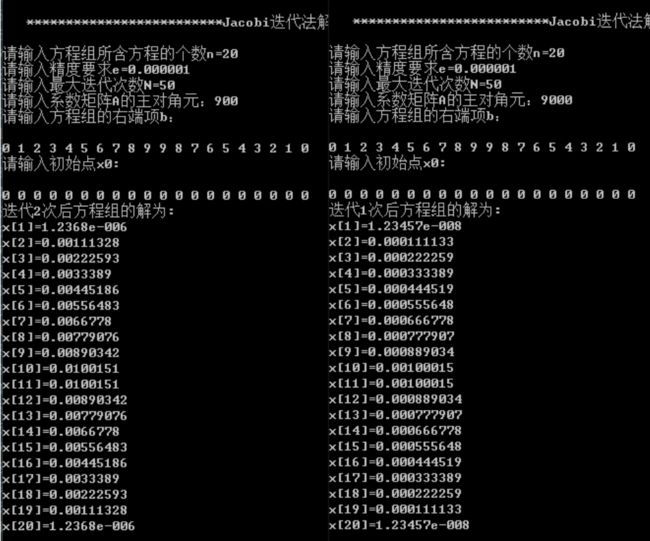
四、 实验内容
- 求矩阵A的LU分解的主函数如下:
L = new double[n];
U = new double[n];
for (int i = 0; i < s; i++)
{
for (int j = 0; j < s; j++)
{
if (i == j)
L[i*s+j] = 1;
if (i < j)
L[i*s+j] = 0;
if (i > j)
U[i*s+j] = 0;
U[0*s+j] = a[0*s+j];
L[i*s+0] = a[i*s+0] / U[0*s+0];
}
}
for (int k = 1; k < s; k++)
{
for (int j = k; j < s; j++)
{
tmp = 0;
for (int m = 0; m < k; m++)
{
tmp += L[k*s+m] * U[m*s+j];
}
U[k*s+j] = a[k*s+j] - tmp;
}
for (int i = k+1; i < s; i++)
{
tmp = 0;
for (int m = 0; m < k; m++)
{
tmp += L[i*s+m] * U[m*s+k];
}
L[i*s+k] = ( a[i*s+k] - tmp ) / U[k*s+k];
}
}
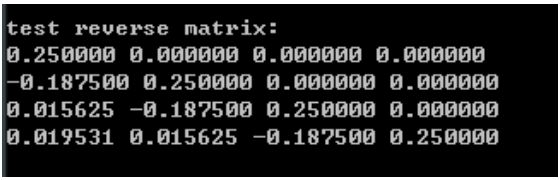
――――――LU矩阵求逆矩阵的代码如下:
//L矩阵求逆
for(int j=0;j { for(int i=j+1;i { double sum=0.0; for(int k=j;k { sum+=Lower[i][k]*ReverseLower[k][j]; } ReverseLower[i][j]=-sum/Lower[i][i]; } } //U矩阵求逆 for(int j=rank-1;j>=1;j--) { for(int i=j-1;i>=0;i--) { double sum=0.0; for(int k=i+1;k<=j;k++) { sum+=Upper[i][k]*ReverseUpper[k][j]; } ReverseUpper[i][j]=-sum/Upper[i][i]; } } void DirectLU(double a[N][N+1],double x[]) { int i,r,k,j; double s[N],t[N];//={-20,8,14,-0.8}; double max; for(r=0;r { max=0; j=r; for(i=r;i { s[i]=a[i][r]; for(k=0;k s[i]-=a[i][k]*a[k][r]; s[i]=s[i]>0?s[i]:-s[i]; //s[i]取绝对值 if(s[i]>max){ j=i; max=s[i]; } } if(j!=r) //选出的主元所在行j若不是r,则对两行相应元素进行调换 { for(i=0;i swap(a[r][i],a[j][i]); } for(i=r;i for(k=0;k a[r][i]-=a[r][k]*a[k][i]; } for(i=r+1;i { for(k=0;k a[i][r]-=a[i][k]*a[k][r]; a[i][r]/=a[r][r]; } } for(i=0;i t[i]=a[i][N]; for(i=N-1;i>=0;i--) //利用回代法求最终解 { for(r=N-1;r>i;r--) t[i]-=a[i][r]*x[r]; x[i]=t[i]/a[i][i]; } } int flag=1; cout<<"输入矩阵A的阶数:"< cin>>M; b[0]=2;c[0]=1;d[0]=-7; for(i=1;i { a[i]=1;b[i]=2;c[i]=1;d[i]=-5; } a[M-1]=1;b[M-1]=2;d[M-1]=-5; for(k=0;k { b[k+1]=b[k+1]-(a[k+1]/b[k])*c[k]; d[k+1]=d[k+1]-(a[k+1]/b[k])*d[k]; } if(flag) { x[M-1]=d[M-1]/b[M-1]; for(i=M-2;i>=0;i--) { s=d[i]; s=s-c[i]*x[i+1]; x[i]=s/b[i]; } cout<<"此方程的解为:"< for(i=0;i { if(i%2==0) cout< cout<<"x["< //system("pause"); } cout< void Jacobi::Iteration() { for(i=0;i sum=0; for(j=0;j if(j!=i) sum+=A[i][j]*x0[j]; if(A[i][i]==0) { cout<<"在迭代过程中,系数矩阵主对角线上的数出现为零的情形,无法继续迭代,程序终止!"< exit(0); } x[i]=(b[i]-sum)/A[i][i]; } Judge(); } void Gauss_Seidel::Iteration() { for(i=0;i sum=sum1=0; for(j=0;j sum+=A[i][j]*x0[j]; for(j=i+1;j sum1+=A[i][j]*x0[j]; if(A[i][i]==0) { cout<<"在迭代过程中,系数矩阵主对角线上的数出现为零的情形,无法继续迭代,程序终止!"< exit(0); } x[i]=(b[i]-sum-sum1)/A[i][i]; } Judge(); } 五、 实验结果 给定矩阵A与向量b ――求A的LU分解; --利用A的LU分解求解下列方程: -Ax = b; -A2x = b; -A3x = b 对iii.,若先求LM = A3,再解LMx = b有何缺点? -―――――――――――――――――――――――――――――――――――――― 当n=10时: ――Ax = b的解为 x =(0 .545454,-0.499999,-3.971573,2.5836,-1.444715,8.344654,-5.188799,2.407111,-3.632159,4.545457)-1 ――A2x = b 的解为 x =(0.549586,-0.772726,0.249998,8.174827,-4.631004,3.457071,-2.65427,9.026667,-2.272733,4.958682)-1 ――A3x = b的解为 x =(0.6883911,-1.172518,0.6363608,-0.1249981,-1.1815,9.874508,-7.902941,1.136398,-4.752079,6.339223)-1 ――――――――――――――――――――――――――――――――――――――― ――利用A的LU分解求解A-1,n值自己选定。 当n=4时:(先求LU分解,分别求L和U的逆矩阵,相乘得A的逆矩阵) 再用现有的LU分解法解此方程组,并对二者进行比较。 由于n=300时的解太多,故将其保存在了“追赶法n=300.txt”中,同样的,n=100时的值也保存在了“追赶法n=100.txt”中 ----选取不同初值x0和不同的b,给定迭代误差用两种迭代法计算,观测得到的迭代向量并分析计算结果给出结论 ----取定x0及b,将A的主对角线元素成倍放大,其他不变,用简单迭代法计算多次,比较收敛速度,分析计算结果并给出结论。 六、 实验结果分析 1. LU分解矩阵可以较高斯消元法更快速地求解出线性方程组 Ax = b 的解,特别对于像题目1中这样的特殊下三角形矩阵,使用LU分解可以得到一个主元为1的下三角形矩阵和一个只有主对角线有统一取值的上三角形矩阵;对于求解使其更加方便,大大减少了高斯消元法的运算量; 同时,也因为这个原因,在求解A 的逆矩阵的时候,先行求出 其LU分解的两个三角形矩阵的逆矩阵,再相乘得到A的逆矩阵,运算量得到了很大的削减,提高了计算效率。 2. 追赶法的基础是LU分解,所以仍然保持了LU分解的特性,是一种特殊的LU分解,充分利用了系数矩阵的特点,使分解变得更为简单,得到对三对角线性方程组的快速解法(随着n的取值的逐渐变大,这两种解法的差距也明显地体现了出来,速度和计算量上,LU分解明显比追赶法要花费大); 因为追赶法的特性,在求解三对角线性方程组时,利用追赶法要远优于LU分解法,可以减少运算量,有效提高计算效率。 3. 由两种不同的迭代法求解题目4中的三对角线性方程组可得,变换不同的初值x0和不同的b,结果的影响基本呈线性变换,受两者影响;固定其中某个值不变只改变另一组时,其可以明显察觉出其中的变化。但是两者迭代方法收敛的速度相差不大,高斯-赛德尔略优于雅克比迭代法; 当取定x0和b,将A的主对角线元素成倍放大,其他不变时,可以明显地看出,A的主对角元素越大,迭代法迭代的次数就越少,也就意味着收敛越快;因为主元在这个方程中起到的影响因素明显变大,其他数值的影响被削弱,更容易找到收敛的结果,迭代次数更少,速度更快; 在题目5中,由②中的特殊结果表明,对于简单的二元方程组,迭代法的实用性明显变差,而且特别依赖于初值的设定,如果初值设定的不正确或者稍有差别,结果就会非常复杂,甚至于偏差只有1,却导致迭代了近200次,结果却越来越差的计算值。所以,对于简单的线性方程组,用简单的高斯消元法反而会更加简单。 -------------------------------------- 因为直接从word实验报告中copy过来的,排版会有些奇怪,不过一些重点的部分已经用截图替换了,应该不会影响阅读 有关的算法程序关键部分已经在实验报告中展示,详细的代码,可以自行补充或者评论私信。