统计学习方法学习笔记

监督学习的两个基本策略：经验风险最小化和结构风险最小化

经验风险最小化例子：最大似然估计（当模型是条件概率分布，损失函数是对数损失函数时，经验风险最小化就等价于极大似然估计）。 但是当样本容量很小时，经验风险最小化学习的效果就未必很好，会产生后面将要叙述的“过拟合”现象。

为了防止过拟合，有了结构风险最小化。例子：最大后验概率估计（MAP）

两种常用模型选择方法：正则化与交叉验证。

学习方法的泛化能力：该方法学习到的模型对未知数据的预测能力。

分类问题：在监督学习中，当输出变量Y取有限个离散值时，预测问题便成为分类问题。

分类器：监督学习从数据中学习一个分类模型或分类决策函数，称为分类器。分类器对新的输入进行输出预测，称为分类，可能的输出称为类。

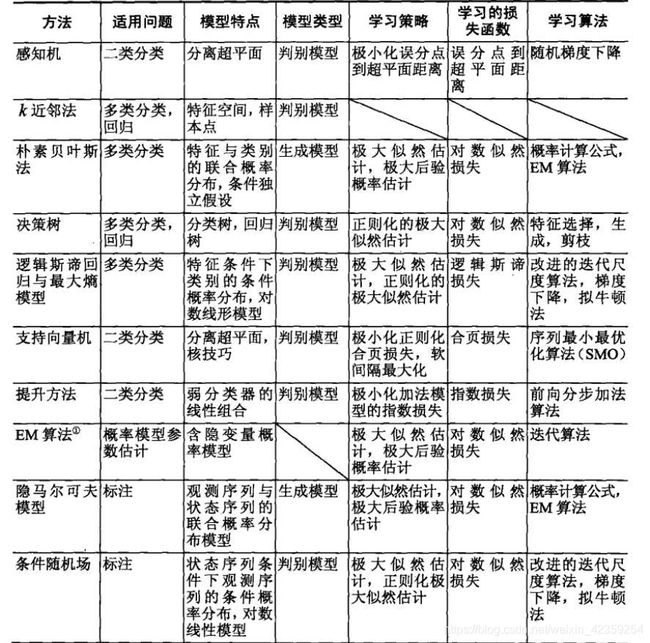
分类问题、标注问题、回归问题都是监督学习的重要问题，我主要学的统计方法包括：感知机，k近邻法，朴素贝叶斯法，决策树，逻辑斯谛回归与最大熵模型、支持向量机、提升方法、EM算法、隐马尔科夫模型和条件随机场。这些方法是主要的分类、标注以及回归方法。他们又可以归类成生成方法与判别方法。

感知机：二类分类的线性分类模型，输入为实例的特征向量，输出为实例的类别，取+1和-1的值。
感知机学习旨在求出将训练数据进行线性划分的分离超平面，所以导入损失函数利用梯度下降法对损失函数进行极小化，求得感知机模型。 感知机分为原始形式和对偶形式，是神经网络和支持向量机的基础。

感知机学习算法存在许多解，这些解及依赖于初值的选择，也依赖于迭代过程中误分类点的选择顺序。为了得到唯一的超平面，需要对分离超平面增加约束条件，这就是线性支持向量机的想法。

k近邻算法：给定一个训练数据集，对新的输入实例，在训练数据中找到与该实例最邻近的k个实例，这k个实例的多数属于某个类，就把该输入实例分为这个类。

k近邻模型由三个基本要素：距离度量、k值的选择和分类决策规则决定。

kd树是一种便于对k维空间中的数据进行快速检索的数据结构，kd树是二叉树，表示对k维空间的一个划分，其每个节点对应于k维空间划分中的一个超矩形区域。利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。

决策树是一种基本的分类与回归方法，学习时利用训练数据，根据损失函数最小化的原则建立决策树模型。预测时，对新的数据，利用决策树模型分类。步骤：特征选择，决策树的生成和决策树的修剪。

支持向量机：二类分类模型。基本模型是定义在特征空间上的间隔最大的线性分类器。间隔最大可以区别于感知机。
SVM还包括核技巧，使他成为实质上的非线性分类器，
SVM的学习策略就是间隔最大化，
SVM的学习算法是求解凸二次规划的最优化算法。
核方法是比SVM更为一般的机器学习的方法。
SVM是在特种空间上进行的。

SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面，对线性可分的训练数据集而言，线性可分分离超平面有无穷多个（等价于感知机），但是几何间隔最大的分离超平面是唯一的，这里的间隔最大化是成为硬间隔最大化。
（与训练数据集近似线性可分的软间隔最大化区分）

间隔最大化：对训练数据集找到几何间隔最大的超平面意味着以充分大的确信度对训练数据进行分类。

核技巧的想法：在学习与预测中只定义核函数而不显式地定义映射函数。

将线性SVM拓展到非线性SVM，只需将线性SVM对偶形式中的内积换成核函数。

SVM的学习问题可以形式化为求解凸二次规划问题，这样的凸二次规划问题具有全局最优解，并且有许多最优化算法可以用于这一问题的求解，但是当训练样本容量很大时，这些算法往往变得非常低效，以致无法使用。常用高效算法：序列最小最优化算法。

提升方法——Adaboost算法 提升树

EM算法是一种迭代算法，用于含有隐变量的概率模型参数的极大似然估计，或者极大后验概率估计。
每次迭代由两步组成：E步，求期望；M步，求极大。所以EM又叫期望极大算法。
隐马尔科夫模型的非监督学习也是EM算法的一个重要应用。

隐马尔科夫模型是关于时序的概率模型，描述一个隐藏的马尔科夫链随机生成不可观测的状态序列，再由各个状态随机生成一个观测而产生观测的序列的过程。