图像分类的卷积神经网络LeNet,VGG,GoogLeNet,ResNet通俗解读及其pytorch实现
在学习深度学习的过程中,曾经遇到过一位行业大佬给我分享他的一个经验。无论哪种模型,他拿到手之后,首先要做的是弄清楚数据的流入和流出形状变化,然后再去研究具体的网络架构。这个思路一直影响着我,因此,本文在讲解CNN结构时会穿插着一条支路,将数据经过每个网络层的维度变化展示出来,以帮助读者更好理解网络结构。
这篇文章有点长,共分为4个部分,分别是LeNet,VGG,GoogLeNet和ResNet,4个章节相互独立,可跳着看。
声明一下,以下图片均来自网络结构对应的原始论文,原始论文连接放在最后面,有兴趣可以自己查阅。
一 LeNet
先从LeNet讲起,是最基础的卷积神经网络。先上图。
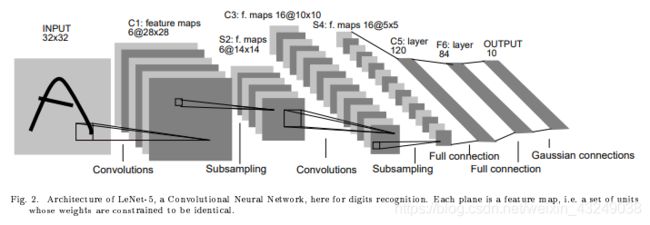
从网络结构图可看出,LeNet共有7层。假设输入为[1,3,32,32],经过 第一层卷积操作之后,形状变为[1,6,28,28]。第一层所用卷积核为filter_size=(5,5)。
第二层为降采样层,降采样层均通过最大池化(maxpooling)进行实现。经过第二层后,输出变为[1,6,14,14]。
第三层为卷积层,经过第三层后输出变为[1,16,10,10]。所用卷积核为filter_size=(5,5)。
第四层为降采样层,输出为[1,16,5,5]。
第五层为全连接层,输出变为一维,共120个神经元,输出为[1,120]。
第六、七层均为全连接层,输出神经元依次变为84,10,输出最后为[1,10]。 10可对应类别共有10类。
下面进行LeNet的实现。
import torch.nn as nn
import torch.nn.functional as F
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16*5*5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
out = F.relu(self.conv1(x))
out = F.max_pool2d(out, 2)
out = F.relu(self.conv2(out))
out = F.max_pool2d(out, 2)
out = out.view(out.size(0), -1)
out = F.relu(self.fc1(out))
out = F.relu(self.fc2(out))
out = self.fc3(out)
return out
到这里LeNet网络就结束了。
二 VGG
接下来讲VGG网络结构。
VGG网络与LeNet一样,同样是由卷积层模块后接全连接层构成。
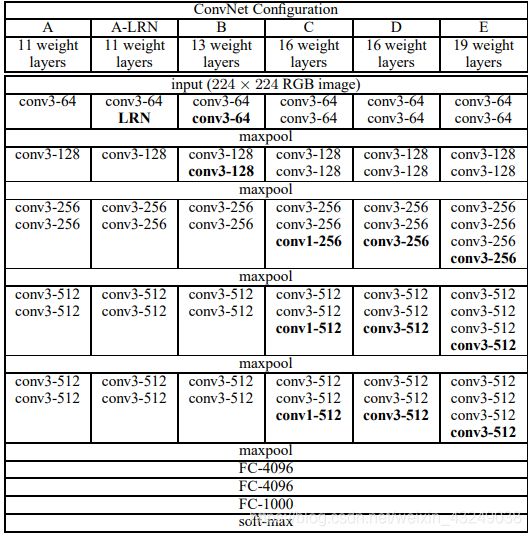
上图是VGG论文中作者贴出的原图。看起来比较复杂,这里和大家解释一下。
VGG根据网络深度不一样,有VGG-11,VGG-13,VGG-16,VGG-19四种网络结构。最初VGG的 设计思想就是通过重复堆叠简单的基础块来构建深度网络模型。记住这个设计思想,理解VGG网络结构会容易很多。
下面上代码实现VGG-11,VGG-13,VGG-16,VGGG-19的实现。
'''VGG11/13/16/19 in Pytorch.'''
import torch
import torch.nn as nn
cfg = {
'VGG11': [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'VGG13': [64, 64, 'M', 128, 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'VGG16': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M'],
'VGG19': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 256, 'M', 512, 512, 512, 512, 'M', 512, 512, 512, 512, 'M'],
}
class VGG(nn.Module):
def __init__(self, vgg_name):
super(VGG, self).__init__()
self.features = self._make_layers(cfg[vgg_name])
self.classifier = nn.Linear(512, 10)
def forward(self, x):
out = out.view(out.size(0), -1)
out = self.classifier(out)
return out
def _make_layers(self, cfg):
layers = []
in_channels = 3
for x in cfg:
if x == 'M':
layers += [nn.MaxPool2d(kernel_size=2, stride=2)]
else:
layers += [nn.Conv2d(in_channels, x, kernel_size=3, padding=1)]
in_channels = x
return nn.Sequential(*layers)
下面以输入[1,3,32,32]为例子梳理下VGG-16的网络结构(对于上图中D列)。
首先讲下_make_layers的函数功能。将cfg中的成员(设为x)依次输入函数_make_layers中,输出特征图大小不改变,通道数变为x;假如从cfg中获得"M",则进行最大池化,此时输出特征图通道数不变,宽和高均减小一半。理解完_make_layers函数的功能后,就能比较方便理解VGG-16网络。
首先
(1)cfg中的’64’进入_make_layers函数中,输出特征图:[1,64,32,32]。
(2)重复(1)步骤,输出特征图:[1,64,32,32];
(3)‘M’进入_make_layers函数中,此时进行最大池化MaxPool2d,输出通道数不变,特征图宽和高减半。输出特征图:[1,64,16,16]。
(4)-(5) '128’进入_make_layers函数中,输出特征图:[1,128,16,16];
(6)‘M’进入_make_layers函数中,此时进行最大池化MaxPool2d,输出通道数不变,特征图宽和高减半。输出特征图:[1,128,8,8]。
(7)(8)(9) '256’进入_make_layers函数中,输出特征图:[1,256,8,8];
(10)‘M’进入_make_layers函数中,此时进行最大池化MaxPool2d,输出通道数不变,特征图宽和高减半。输出特征图:[1,256,4,4]。
(11-13) '512’进入_make_layers函数中,输出特征图:[1,512,4,4];
(14)‘M’进入_make_layers函数中,此时进行最大池化MaxPool2d,输出通道数不变,特征图宽和高减半。输出特征图:[1,512,2,2]。
(15-17) '512’进入_make_layers函数中,输出特征图:[1,512,2,2];
(18)‘M’进入_make_layers函数中,此时进行最大池化MaxPool2d,输出通道数不变,特征图宽和高减半。输出特征图:[1,512,1,1]。
(19)全连接层,先将输入特征图转为一维模式,再进行全连接,输出特征图[1,10]。
这里注解一下,这里VGG-16是根据上图中的D列来实现的。D列中的16层哪里来的呢,是13个CNN卷积层+3个FC层得来的。FC层的设计根据实际情况设计。论文原文中因为要实现数据集的1000类分类,因此最后一层是FC-1000,我这里把三层FC层缩减为了FC-10,原因是我实际中做的是CIFAR数据集的10分类,这里的代码搭建的网络结构和论文中那张图并不完全一致,只需大家能理解VGG结构就行。
讲到这里,大家应该对图像分类的基本网络结构有了一定的了解了。目前为止的LeNet网络和VGG网络都是中规中矩的CNN网络,便于理解。下面开始讲解的GoogLeNet网络和ResNet网络则对普通的CNN网络做了结构上的改进。
三 GoogleNet
GoogLeNet在2014年的ImageNet比赛中表现亮眼。GoogLeNet网络中结构上的创新点在于使用了含并行连接的网络。我也一再强调过,单纯学习网络结构意义并不大,要深入理解网络中所包含的设计思想。
这里大家注意以下GoogLeNet的写法,中间那个字母’L’是大写的,是为了向LeNet致敬的原因,所以这样起名ヽ(✿゚▽゚)ノ。
老规矩,先上图,这是GoogLeNet中基础模块Inception块,并行连接的思想在Inception块中体现的淋漓尽致。
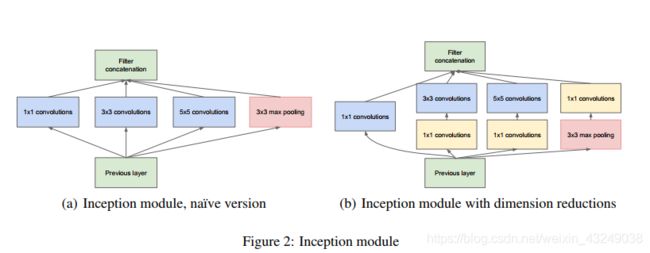
由上图可看出,Inception块(这里讲解右边的版本)共有4条并行的线路,其中前3条线路分别使用1x1,3x3,5x5的卷积层,以获取不同空间下尺寸的信息。第4条线路则采用3x3最大池化层+1x1卷积层。注意,4条线路在此过程中都使用了合适的填充来使得输入和输出的高和宽一致,这样做的目的是方便4条线路的合并。
下面是实现Inception块的代码。
class Inception(nn.Module):
def __init__(self, ch_in, n1, n3, n3_out, n5, n5_out, pool_planes):
super(Inception, self).__init__()
# 1x1 conv branch
self.b1 = nn.Sequential(
nn.Conv2d(ch_in, n1, kernel_size=1),
nn.BatchNorm2d(n1),
nn.ReLU(True),
)
# 1x1 conv -> 3x3 conv branch
self.b2 = nn.Sequential(
nn.Conv2d(ch_in, n3, kernel_size=1),
nn.BatchNorm2d(n3),
nn.ReLU(True),
nn.Conv2d(n3, n3_out, kernel_size=3, padding=1),
nn.BatchNorm2d(n3_out),
nn.ReLU(True),
)
# 1x1 conv -> 5x5 conv branch
self.b3 = nn.Sequential(
nn.Conv2d(ch_in, n5red, kernel_size=1),
nn.BatchNorm2d(n5),
nn.ReLU(True),
nn.Conv2d(n5, n5_out, kernel_size=3, padding=1),
nn.BatchNorm2d(n5x5),
nn.ReLU(True),
)
# 3x3 pool -> 1x1 conv branch
self.b4 = nn.Sequential(
nn.MaxPool2d(3, stride=1, padding=1),
nn.Conv2d(ch_in, pool_planes, kernel_size=1),
nn.BatchNorm2d(pool_planes),
nn.ReLU(True),
)
def forward(self, x):
y1 = self.b1(x)
y2 = self.b2(x)
y3 = self.b3(x)
y4 = self.b4(x)
return torch.cat([y1, y2, y3, y4], 1)
注解,这里在每一层卷积层后都进行了批量归一化(batchnorm)处理,批量归一化的优点是加速模型学习速度,缓解梯度消失问题,且具有一定的正则化效果。这里看不懂没关系,不影响本文的阅读。
接下来我们用数据流向讲解Inception块。假设前一层的输入为[1,3,32,32]。
设置参数为Inception(3,64,96,128,16,32,32)。
则第一条线路,经过1x1卷积层,输出特征图:[1,64,32,32]。
第二条线路,经过1x1卷积和3x3卷积层后,输出特征图[1,128,32,32]。
第三条线路,经过1x1和5x5卷积后,输出特征图[1,32,32,32]。
第四条线路,经过3x3最大池化和1x1卷积后,输出特征图[1,32,32,32,]。
最后四条线路相加,由于在torch.cat()中设置维度为1,因此在通道层将四条线路结果相连结,得到最后总结果:[1,64+128+32+32,32,32]=[1,256,32,32]。
总结以下Inception函数对数据维度改变的作用:输出特征图通道数是Inception输入参数第2个,第4个,第6个,第7个之和。
看到这里应该对Inception块有了充分的认识了。
接下来,上GoogLeNet网络主题结构图。有点长,此处感谢qq提供的长截图功能。
在讲完Inception模块后,我们继续讲解GoogLeNet模块。
下面上GoogLeNet的实现代码。
class GoogLeNet(nn.Module):
def __init__(self):
super(GoogLeNet, self).__init__()
self.pre_layers = nn.Sequential(
nn.Conv2d(3, 192, kernel_size=3, padding=1),
nn.BatchNorm2d(192),
nn.ReLU(True),
)
self.a3 = Inception(192, 64, 96, 128, 16, 32, 32)
self.b3 = Inception(256, 128, 128, 192, 32, 96, 64)
self.maxpool = nn.MaxPool2d(3, stride=2, padding=1)
self.a4 = Inception(480, 192, 96, 208, 16, 48, 64)
self.b4 = Inception(512, 160, 112, 224, 24, 64, 64)
self.c4 = Inception(512, 128, 128, 256, 24, 64, 64)
self.d4 = Inception(512, 112, 144, 288, 32, 64, 64)
self.e4 = Inception(528, 256, 160, 320, 32, 128, 128)
self.a5 = Inception(832, 256, 160, 320, 32, 128, 128)
self.b5 = Inception(832, 384, 192, 384, 48, 128, 128)
self.avgpool = nn.AvgPool2d(8, stride=1)
self.linear = nn.Linear(1024, 10)
def forward(self, x):
out = self.pre_layers(x)
out = self.a3(out)
out = self.b3(out)
out = self.maxpool(out)
out = self.a4(out)
out = self.b4(out)
out = self.c4(out)
out = self.d4(out)
out = self.e4(out)
out = self.maxpool(out)
out = self.a5(out)
out = self.b5(out)
out = self.avgpool(out)
out = out.view(out.size(0), -1)
out = self.linear(out)
return out
虽然网络结构看起来非常复杂,然而代码实现就简单多了。
从网络结构图中可看出,共有9个Inception模块。在代码中分别是a3,b3,a4,b4,c4,d4,e4,a5,b5。
我们将GoogLeNet共分为五个部分。假设输入维度[1,3,32,32]。
GoogLeNet模块第一部分为代码中的pre_layers,由一个卷积层和1个BatchNorm组成,输出特征图[1,192,32,32]
GoogLeNet模块第二部分串联了2个完整的Inception模块个一个最大池化层,第一个Inception模块的输出通道数为64+128+32+32=256,4条线路的输出通道数之比为2:4:1:1。第二个Inception模块的输出通道数为128+192+96+64=480,4条线路的输出通道数之比为4:6:3:2。
经过第一部分后,输出特征图[1,480,16,16]
第三部分串联了5个Inception和一个最大池化层。
其输出通道数分别是192+208+48+64=512,160+224+64+64=512,128+256+64+64=512,112+288+64+64=528,256+320+128+128=832。
经过第二部分之后,输出特征图[1,832,8,8]。
第四部分串联了2个Inception块和一个平均池化层。输出通道数分别为256+320+128+128=832,384+384+128+128=1024。
输出特征图[1,1024,1,1]
第五部分为1个全连接层,输出特征图[1,10]。10为分类类别数。(注意,这里同样没有按照论文中的结构图搭建,主要是让大家明白GoogLeNet的设计特点和实现方法就行)。
四 ResNet
终于讲到ResNet了,也是这个系列的完结篇。
ResNet的应用非常广泛,除了在图像分类领域大放异彩之外,还在目标检测领域中也被广泛使用,例如著名的YOLO模型就用到了它。
ResNet的引出,我们可以先思考一个问题:神经网络的层数越深,是否意味这训练误差会更小。即我们是否能够通过不断叠加神经网络层数的方式来取得更好的效果。
ResNet论文中也给出了相应的答案,如下图:
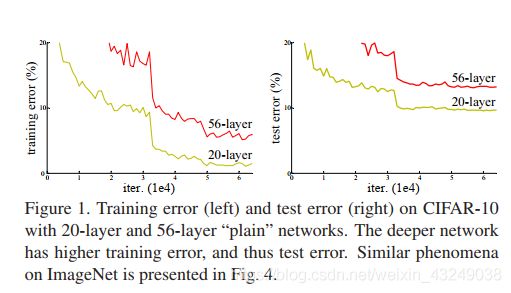
可以看出答案是否定的。56层的网络无论训练误差还是测试误差均大于20层的网络。正是为了解决这个退化问题,ResNet网络结构被提出。
下面再看下ResNet 设计思想。
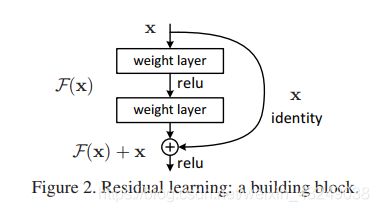
ResNet网络的精髓就在于加了一条从输入到输出的捷径,也是残差网络名字的由来。
再上ResNet整体网络结构图与VGG的对比。
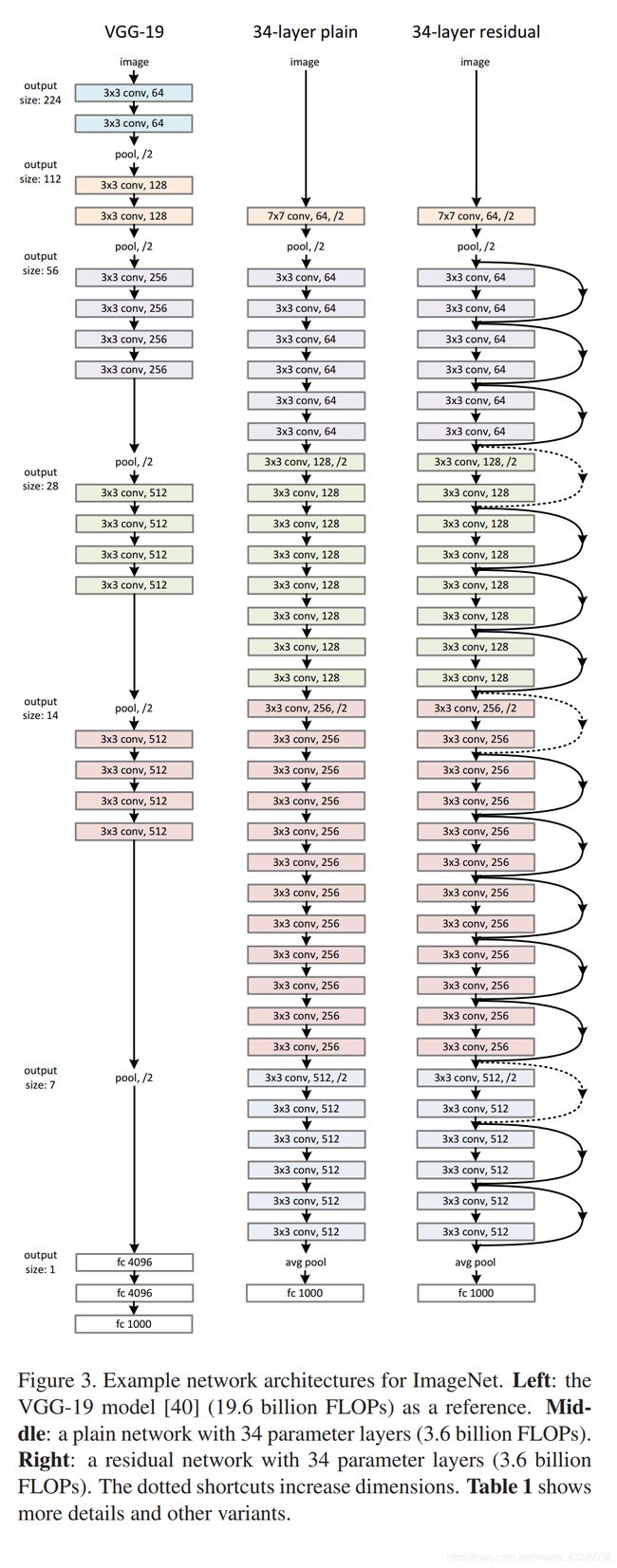 左边是VGG-19的网络结构,中间是与ResNet层数相同的靠数量堆积的CNN结构。右边是我们的主角,一个34层的ResNet结构。下面上ResNet网络结构BasicBlock模块,即残差块代码:
左边是VGG-19的网络结构,中间是与ResNet层数相同的靠数量堆积的CNN结构。右边是我们的主角,一个34层的ResNet结构。下面上ResNet网络结构BasicBlock模块,即残差块代码:
import torch
import torch.nn as nn
import torch.nn.functional as F
class BasicBlock(nn.Module):# tow 3*3 filters conv
expansion = 1
def __init__(self, in_planes, planes, stride=1):
super(BasicBlock, self).__init__()
self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=3, stride=stride, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(planes)
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes)
self.shortcut = nn.Sequential()
if stride != 1 or in_planes != self.expansion * planes:
self.shortcut = nn.Sequential(
nn.Conv2d(in_planes, self.expansion * planes, kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(self.expansion * planes)
)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.bn2(self.conv2(out))
out += self.shortcut(x)
out = F.relu(out)
return out
一个基本的BasicBlock块首先有两个相同输出通道的3x3卷积层。每个卷积层后接一个批量归一化层和ReLU激活函数。经过两层卷积后,直接加上为经过卷积的输入。注意,这样的设计则要求两层卷积层不会改变输入与输出特征图的宽和高。
更重要的一点是,ResNet结构中原始输入和卷积层的相加和GoogLeNet中不同线路的连结有着本质区别。在GoogLeNet中,不同线路的连结仅仅是在通道,即第二个维度将特征图连接起来,而ResNet中则是在特征图的宽和高上进行加法运算。
BasicBlock输入参数共有两个,in_planes和planes,作用可以看作是将输入通道数为in_planes的特征图转换成通道数为planes的特征图,其中特征图宽和高并不改变。
定义完残差块后便可直接定义ResNet网络了。
class ResNet(nn.Module):
def __init__(self, num_blocks, num_classes=10):
super(ResNet, self).__init__()
self.in_planes = 64
self.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(64)
self.layer1 = self._make_layer(64, num_blocks[0], stride=1)
self.layer2 = self._make_layer(128, num_blocks[1], stride=2)
self.layer3 = self._make_layer(256, num_blocks[2], stride=2)
self.layer4 = self._make_layer( 512, num_blocks[3], stride=2)
self.linear = nn.Linear(512 * BasicBlock.expansion, num_classes)
def _make_layer(self, planes, num_blocks, stride):
strides = [stride] + [1] * (num_blocks - 1)
layers = []
for stride in strides:
layers.append(BasicBlock(self.in_planes, planes, stride))
self.in_planes = planes * BasicBlock.expansion
return nn.Sequential(*layers)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.layer1(out)
out = self.layer2(out)
out = self.layer3(out)
out = self.layer4(out)
out = F.avg_pool2d(out, 4)
out = out.view(out.size(0), -1)
out = self.linear(out)
return out
这里先讲下代码中的_make_layer函数功能,否则会影响对代码的解读。我们可以看到,_make_layer函数共有3个输入参数,planes,num_blocks,stride。strides是一个list,将stride的初始值和num_blocks-1个1组合成一个list。例如,假设stride=2,num_blocks=3,则第一次执行_make_layer函数时,strides=[2,1,1]。layers则是将num_blocks个BasicBlock叠加到一起的网络结构。注意,若strides中含有元素2时,输出特征图宽和高均减半。
下面来解析ResNet网络结构。假设输入维度[1,3,32,32]。
首先,将原始输入经过一个filter_size=3x3,stride=1,padding=1的卷积层,随后进行批量归一化处理。输出特征图[1,64,32,32]。
接下来,则来到了layer1层。这一层将通过3个BasicBlock模块,每个BaiscBlock中的stride均为1。
输出特征图[1,64,32,32]。
layer2层,通过4个BasicBlock模块,strides [2,1,1,1]。输出特征图[1,128,16,16]
layer3层,通过6个BasicBlock模块,strides [2,1,1,1,1,1]
输出特征图[1,256,8,8]
layer4层,4个BasicBlock模块,strides[2,1,1,1]
输出特征图[1,512,4,4]。
再经过平均池化层处理输出特征图[1,512,1,1]。
最后全连接FC层处理,输出特征图[1,10],用于分类。
注意,这里所搭建网络结构同样与原论文不一致,重在促进对ResNet设计思想的理解和框架构建。
文章中如有不对的地方,希望大家留言改正。作者和大家一起进步。
参考资料:
- LeNet论文,http://yann.lecun.com/exdb/publis/pdf/lecun-98.pdf。
- VGG论文,https://arxiv.org/pdf/1409.1556.pdf。
- GoogLeNet论文,https://arxiv.org/abs/1409.4842.pdf
- ResNet论文,https://arxiv.org/abs/1512.03385.pdf
- 参考代码原自这个网址:https://github.com/karanchahal/distiller/tree/51da39a359d7604fcfadf6dc42fe3cd8a894418e/models/cifar10