非线性方程的数值解法
设有一个单变量的非线性方程 f ( x ) = 0 f(x) = 0 f(x)=0,往往这样的方程没有直接的求根公式,因此没有直接方法计算,只能使用迭代法来求数值解,二分法就是这样的一种方法,这里介绍一下其他的几种方法
不动点迭代法
我们可以将非线性方程 f ( x ) = 0 f(x) = 0 f(x)=0改写为 x = ϕ ( x ) x = \phi(x) x=ϕ(x),满足这样式子的x称作 ϕ ( x ) \phi(x) ϕ(x)的一个不动点,求 f ( x ) f(x) f(x)的零点就等价于求 ϕ ( x ) \phi(x) ϕ(x)的不动点,可以选定一个初始值 x 0 x_0 x0代入等式的右侧,然后一直以 x k + 1 = ϕ ( x k ) x_{k+1} = \phi(x_k) xk+1=ϕ(xk)的方式迭代下去,这样可以获得一个序列,如果序列 { x k } \{x_k\} {xk}有极限: lim k − > ∞ x k = x ∗ \lim_{k->\infty}x_k = x^* k−>∞limxk=x∗则称该迭代法为不动点迭代法。
我们可以用几何图像来表达不动点迭代法的思想:
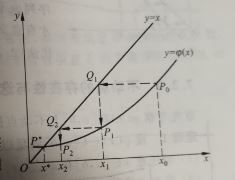
如图,选定了初始值 x 0 x_0 x0,然后计算出 ϕ ( x 0 ) \phi(x_0) ϕ(x0)得到了 P 0 P_0 P0,然后再过 ( x 0 , P 0 ) (x_0,P_0) (x0,P0)引一条与x轴平行的直线,它与直线 y = x y=x y=x交于点 Q 1 ( P 0 , P 0 ) Q_1(P_0,P_0) Q1(P0,P0),然令 x 1 = P 0 x_1 = P_0 x1=P0,沿着图上的路径继续走下去,可以发现最终点列 { P k } \{P_k\} {Pk}会收敛到 P ∗ P^* P∗,也就是最终迭代的值 x k x_k xk会收敛到想要的 x ∗ x^* x∗。
尽管在这个图上最终的结果是收敛的,但是这并不意味着采用不动点迭代法一定是收敛的
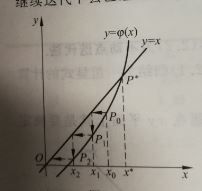
例如在这个图上,用不动点迭代法就是不收敛的,点列 { P k } \{P_k\} {Pk}会一直往偏离 P ∗ P^* P∗的方向移动。
不动点的存在性和迭代的收敛性
首先考虑 ϕ ( x ) \phi(x) ϕ(x)在 [ a , b ] [a,b] [a,b]上不动点的存在性和唯一性:
定理1:若 ϕ ( x ) \phi(x) ϕ(x)在 [ a , b ] [a,b] [a,b]上满足:
(1)对于任意的 x ∈ C [ a , b ] x∈C[a,b] x∈C[a,b],都有 a < = ϕ ( x ) < = b a<=\phi(x)<=b a<=ϕ(x)<=b
(2)存在正常数 L < 1 L < 1 L<1,使对任意的 x , y ∈ [ a , b ] x,y∈[a,b] x,y∈[a,b],都有 ∣ ϕ ( x ) − ϕ ( y ) ∣ < = L ∣ x − y ∣ |\phi(x)-\phi(y)|<=L|x-y| ∣ϕ(x)−ϕ(y)∣<=L∣x−y∣
那么 ϕ ( x ) \phi(x) ϕ(x)在 [ a , b ] [a,b] [a,b]上存在唯一的不动点 x ∗ x^* x∗
证:
若 ϕ ( a ) = a \phi(a) = a ϕ(a)=a或 ϕ ( b ) = b \phi(b) = b ϕ(b)=b 那么不动点显然存在
若 ϕ ( a ) > a \phi(a) > a ϕ(a)>a且 ϕ ( b ) < b \phi(b) < b ϕ(b)<b,则设函数 f ( x ) = ϕ ( x ) − x f(x) = \phi(x) - x f(x)=ϕ(x)−x
由已知有 f ( a ) = ϕ ( a ) − a > 0 f(a) = \phi(a) - a > 0 f(a)=ϕ(a)−a>0, f ( b ) = ϕ ( b ) − b < 0 f(b) = \phi(b) - b < 0 f(b)=ϕ(b)−b<0,由连续函数的性质可知,存在 x ∗ ∈ ( a , b ) x^*∈(a,b) x∗∈(a,b)使得 f ( x ∗ ) = 0 f(x^*) = 0 f(x∗)=0
因此不动点一定存在,下面证其唯一性:
设 x 1 ∗ , x 2 ∗ x_1^*,x_2^* x1∗,x2∗都是 ϕ ( x ) \phi(x) ϕ(x)在 ( a , b ) (a,b) (a,b)上的不动点,则由条件(2)可知: ∣ x 1 ∗ − x 2 ∗ ∣ = ∣ ϕ ( x 1 ∗ ) − ϕ ( x 2 ∗ ) ∣ < L ∣ x 1 ∗ − x 2 ∗ ∣ < ∣ x 1 ∗ − x 2 ∗ ∣ |x_1^*-x_2^*| = |\phi(x_1*) - \phi(x_2*)| < L|x_1^*-x_2^*| <|x_1^*-x_2^*| ∣x1∗−x2∗∣=∣ϕ(x1∗)−ϕ(x2∗)∣<L∣x1∗−x2∗∣<∣x1∗−x2∗∣ ,矛盾
因此不动点唯一。
定理2:
设 ϕ ( x ) ∈ C [ a , b ] \phi(x)∈C[a,b] ϕ(x)∈C[a,b]满足定理1中的两个条件,则对于任意选定的 x 0 ∈ [ a , b ] x_0∈[a,b] x0∈[a,b],得到的迭代序列 { x k } \{x_k\} {xk}均收敛到 ϕ ( x ) \phi(x) ϕ(x)的不动点 x ∗ x^* x∗,并且有误差估计: ∣ x k − x ∗ ∣ < = L k 1 − L ∣ x 1 − x 0 ∣ |x_k - x^*| <= \frac{L^k}{1-L}|x_1 - x_0| ∣xk−x∗∣<=1−LLk∣x1−x0∣
证:由条件1可知: { x k } ⊂ [ a , b ] \{x_k\}\subset[a,b] {xk}⊂[a,b] ∣ x k − x ∗ ∣ = ∣ ϕ ( x k − 1 ) − ϕ ( x ∗ ) ∣ < = L ∣ x k − 1 − x ∗ ∣ < = L k ∣ x 0 − x ∗ ∣ |x_k-x^*|=|\phi(x_{k-1})-\phi(x^*)| <= L|x_{k-1} - x^*| <=L^k|x_0-x^*| ∣xk−x∗∣=∣ϕ(xk−1)−ϕ(x∗)∣<=L∣xk−1−x∗∣<=Lk∣x0−x∗∣因为 0 < L < 1 0<L<1 0<L<1,因此当 k − > ∞ k->\infty k−>∞时, { x k } \{x_k\} {xk}收敛到 x ∗ x^* x∗
下面再证明误差估计: ∣ x k + 1 − x k ∣ = ∣ ϕ ( x k ) − ϕ ( x k − 1 ) ∣ < = L ∣ x k − x k − 1 ∣ |x_{k+1}-x_k| = |\phi(x_k) - \phi(x_{k-1})|<=L|x_k-x_{k-1}| ∣xk+1−xk∣=∣ϕ(xk)−ϕ(xk−1)∣<=L∣xk−xk−1∣如此反复地递推有 ∣ x k + 1 − x k ∣ < = L k ∣ x 1 − x 0 ∣ |x_{k+1}-x_k|<=L^k|x_1-x_0| ∣xk+1−xk∣<=Lk∣x1−x0∣
于是对于任意的正整数P都有: ∣ x k + p − x k ∣ < = ∣ x k + p − x k + p − 1 ∣ |x_{k+p}-x_k|<=|x_{k+p}-x_{k+p-1}| ∣xk+p−xk∣<=∣xk+p−xk+p−1∣ + ∣ x k + p − 1 − x k + p − 2 ∣ + ⋅ ⋅ ⋅ + ∣ x k + 1 − x k ∣ +|x_{k+p-1}-x_{k+p-2}|+···+|x_{k+1}-x_k| +∣xk+p−1−xk+p−2∣+⋅⋅⋅+∣xk+1−xk∣ < = ( L k + p − 1 + L k + p − 2 + ⋅ ⋅ ⋅ + L k ) ∣ x 1 − x 0 ∣ < = L k 1 − L ∣ x 1 − x 0 ∣ <=(L^{k+p-1}+L^{k+p-2}+···+L^k)|x_1-x_0|<=\frac{L^k}{1-L}|x_1-x_0| <=(Lk+p−1+Lk+p−2+⋅⋅⋅+Lk)∣x1−x0∣<=1−LLk∣x1−x0∣
在上式中将 p − > ∞ p->\infty p−>∞,由于 x k + p − > x ∗ x_{k+p}->x^* xk+p−>x∗,即可得误差估计式。
在实际计算中往往需要按照精度要求来控制迭代的次数,上述误差估计式原则上是可以用来确定迭代次数的,但是由于其带有信息 L L L,而 L L L往往是不容易确定的,因此我们可以考察相邻两次迭代的偏差: ∣ x k + p − x k ∣ < = ( L p − 1 + L p − 2 + ⋅ ⋅ + 1 ) ∣ x k + 1 − x k ∣ < = 1 1 − L ∣ x k + 1 − x k ∣ |x_{k+p}-x_k|<=(L^{p-1}+L^{p-2}+··+1)|x_{k+1}-x_k|<=\frac{1}{1-L}|x_{k+1}-x_{k}| ∣xk+p−xk∣<=(Lp−1+Lp−2+⋅⋅+1)∣xk+1−xk∣<=1−L1∣xk+1−xk∣
因此只需要确保相邻两次迭代结果的偏差 ∣ x k + 1 − x k ∣ |x_{k+1}-x_k| ∣xk+1−xk∣,如果它足够小的话就可以确保近似值 x k x_k xk具有足够的精度。
还有一个问题就是上述定理所需要的条件往往也不容易确定,如果说 ϕ ( x ) ∈ C [ a , b ] \phi(x) ∈C[a,b] ϕ(x)∈C[a,b],且对于任意的 x ∈ [ a , b ] x∈[a,b] x∈[a,b]都有 ∣ ϕ ′ ( x ) ∣ < = L < 1 |\phi'(x)|<=L<1 ∣ϕ′(x)∣<=L<1则由中值定理可知:对于任意 x , y ∈ [ a , b ] x,y∈[a,b] x,y∈[a,b]有 ∣ ϕ ( x ) − ϕ ( y ) ∣ = ∣ ϕ ′ ( c ) ( x − y ) ∣ < = L ∣ x − y ∣ ( c ∈ ( a , b ) ) |\phi(x)-\phi(y)|=|\phi'(c)(x-y)|<=L|x-y|(c∈(a,b)) ∣ϕ(x)−ϕ(y)∣=∣ϕ′(c)(x−y)∣<=L∣x−y∣(c∈(a,b))
因此在定理中的条件(2)可以用上式来代替。
局部收敛性与收敛阶
上面给出了 x 0 x_0 x0取自区间 [ a , b ] [a,b] [a,b]上时所产生的迭代序列 { x k } \{x_k\} {xk}的收敛性,通常称为全局收敛性,而在实际应用中,往往只需要不动点 x ∗ x^* x∗的邻近的某个区间内的收敛性,即局部收敛性。
设 ϕ ( x ) \phi(x) ϕ(x)具有不动点 x ∗ x^* x∗,如果存在 x ∗ x^* x∗的某个邻域 R : ∣ x − x k ∣ < = δ R:|x-x_k|<=\delta R:∣x−xk∣<=δ,对于任意的 x 0 ∈ R x_0∈R x0∈R,用不动点迭代法产生的序列 { x k } ⊂ R \{x_k\}\subset R {xk}⊂R,且收敛到 x ∗ x^* x∗,则称不动点迭代法局部收敛。
不难得出,如果 x ∗ x^* x∗为 ϕ ( x ) \phi(x) ϕ(x)的不动点, ϕ ′ ( x ) \phi'(x) ϕ′(x)在 x ∗ x^* x∗的某个邻域内连续,且 ∣ ϕ ′ ( x ∗ ) ∣ < 1 |\phi'(x^*)|<1 ∣ϕ′(x∗)∣<1,则迭代法收敛。
来看一个具体的不动点迭代法的例子:求方程 x 2 − 3 = 0 x^2-3=0 x2−3=0的根
我们要对这个方程做变换,转化为 x = ϕ ( x ) x=\phi(x) x=ϕ(x)的形式,显然我们有很多种变换的手段:
(1) x k + 1 = x k 2 + x k − 3 x_{k+1}=x_k^2+x_k-3 xk+1=xk2+xk−3
(2) x k + 1 = 3 x k x_{k+1}=\frac{3}{x_k} xk+1=xk3
(3) x k + 1 = x k − 1 4 ( x k 2 − 3 ) x_{k+1} = x_k - \frac{1}{4}(x_k^2-3) xk+1=xk−41(xk2−3)
(4) x k + 1 = 1 2 ( x k + 3 x k ) x_{k+1} =\frac{1}{2}(x_k+\frac{3}{x_k}) xk+1=21(xk+xk3)
但是要注意到(1)(2)都是不满足上述收敛条件的,因此如果采用(1)(2)的方法是得不到最终的结果的,而对于(3)(4),经过实际运算可以发现,它们收敛到最终结果 x ∗ = 3 x^*=\sqrt{3} x∗=3的速度有差异,现在来考察使用不动点迭代法的收敛速度问题。
设迭代过程 x k + 1 = ϕ ( x ) x_{k+1} = \phi(x) xk+1=ϕ(x)收敛,如果当 k − > ∞ k->\infty k−>∞时迭代误差 e k = x k − x ∗ e_k=x_k-x^* ek=xk−x∗满足渐进关系式: e k + 1 e k p − > C , C ≠ 0 \frac{e_{k+1}}{e_k^p}->C,C≠0 ekpek+1−>C,C̸=0。
则称该迭代过程是P阶收敛的,特别地当 p = 1 ( ∣ C ∣ < 1 ) p=1(|C|<1) p=1(∣C∣<1)时,称为线性收敛, p > ! p>! p>!时为超线性收敛。
定理对于迭代过程 x k + 1 = ϕ ( x k ) x_{k+1}=\phi(x_k) xk+1=ϕ(xk)及正整数p,如果 ϕ ( p ) ( x ) \phi^{(p)}(x) ϕ(p)(x)在锁求根 x ∗ x^* x∗附近连续,并且 ϕ ′ ( x ∗ ) = ϕ ′ ′ ( x ∗ ) = ⋅ ⋅ ⋅ = ϕ ( p − 1 ) ( x ∗ ) = 0 , ϕ ( p ) ( x ∗ ) ≠ 0 \phi'(x^*)=\phi''(x^*)=···=\phi^{(p-1)}(x^*)=0,\phi^{(p)}(x^*)≠0 ϕ′(x∗)=ϕ′′(x∗)=⋅⋅⋅=ϕ(p−1)(x∗)=0,ϕ(p)(x∗)̸=0
则该迭代过程是P阶收敛的。
证:由于 ϕ ′ ( x ∗ ) = 0 \phi'(x^*)=0 ϕ′(x∗)=0,因此可以断定迭代过程具有局部收敛性。
ϕ ( x k ) = ϕ ( x ∗ ) + ϕ ( p ) ( c ) P ! ( x k − x ∗ ) p , c ∈ ( x k , x ∗ ) \phi(x_k)=\phi(x^*)+\frac{\phi^{(p)}(c)}{P!}(x_k-x^*)^p,c∈(x_k,x^*) ϕ(xk)=ϕ(x∗)+P!ϕ(p)(c)(xk−x∗)p,c∈(xk,x∗)
注意到 ϕ ( x k ) = x k + 1 , ϕ ( x ∗ ) = x ∗ \phi(x_k)=x_{k+1},\phi(x^*)=x^* ϕ(xk)=xk+1,ϕ(x∗)=x∗,由上式得: x k + 1 − x ∗ = ϕ p ( c ) P ! ( x k − x ∗ ) p x_{k+1}-x^*=\frac{\phi^{p}(c)}{P!}(x_k-x^*)^p xk+1−x∗=P!ϕp(c)(xk−x∗)p因此 e k + 1 e k p − > ϕ ( p ) ( c ) P ! \frac{e_{k+1}}{e_k^p}->\frac{\phi^{(p)}(c)}{P!} ekpek+1−>P!ϕ(p)(c),这表明迭代过程是P阶收敛的。
可以发现在上面的例子中,(3)是线性收敛的,而(4)是二阶收敛的,因此(4)要快于(3)。
牛顿法
对于线性方程的求根是非常容易的,可以将非线性方程近似地看做线性方程,这就是牛顿法的思想:将 f ( x ) f(x) f(x)在 x k x_k xk处泰勒展开, f ( x ) ≈ f ( x k ) + f ′ ( x k ) ( x − x k ) f(x)≈f(x_k)+f'(x_k)(x-x_k) f(x)≈f(xk)+f′(xk)(x−xk)于是 f ( x ) = 0 f(x)=0 f(x)=0就可以近似地表示为 f ( x k ) + f ′ ( x k ) ( x − x k ) = 0 f(x_k)+f'(x_k)(x-x_k)=0 f(xk)+f′(xk)(x−xk)=0这是一个线性方程,其根为 x k + 1 = x k − f ( x k ) f ′ ( x k ) x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)} xk+1=xk−f′(xk)f(xk)
于是可以将其转化为不动点迭代法,迭代函数为: ϕ ( x ) = x − f ( x ) f ′ ( x ) \phi(x)=x-\frac{f(x)}{f'(x)} ϕ(x)=x−f′(x)f(x)
由于 ϕ ′ ( x ) = f ( x ) f ′ ′ ( x ) [ f ′ ( x ) ] 2 \phi'(x)=\frac{f(x)f''(x)}{[f'(x)]^2} ϕ′(x)=[f′(x)]2f(x)f′′(x),假设 x ∗ x^* x∗是 f ( x ) f(x) f(x)的一个单根,即 f ( x ∗ ) = 0 , f ′ ( x ∗ ) ≠ 0 f(x^*)=0,f'(x^*)≠0 f(x∗)=0,f′(x∗)̸=0,因此 ϕ ′ ( x ∗ ) = 0 \phi'(x^*)=0 ϕ′(x∗)=0,而由于 x ∗ x^* x∗仅是一个单根,因此 f ′ ′ ( x ∗ ) ≠ 0 f''(x^*)≠0 f′′(x∗)̸=0,于是 ϕ ′ ′ ( x ∗ ) = f ′ ′ ( x ∗ ) f ′ ( x ∗ ) ≠ 0 \phi''(x^*)=\frac{f''(x^*)}{f'(x^*)}≠0 ϕ′′(x∗)=f′(x∗)f′′(x∗)̸=0,即牛顿法在 x ∗ x^* x∗邻近是平方收敛的。
牛顿下山法
尽管牛顿法的收敛速度很快,但其收敛性依赖于初值 x 0 x_0 x0的选取,如果 x 0 x_0 x0偏离 x ∗ x^* x∗比较远的话,牛顿法很有可能会发散,为了防止发散,可以在迭代过程中附加一项要求: ∣ f ( x k + 1 ) ∣ < ∣ f ( x k ) ∣ |f(x_{k+1})|<|f(x_k)| ∣f(xk+1)∣<∣f(xk)∣注意是 f ( x ) f(x) f(x),不是 ϕ ( x ) \phi(x) ϕ(x)。
为此将牛顿法的计算结果: x k + 1 ‾ = x k − f ( x k ) f ′ ( x k ) \overline{x_{k+1}}=x_k-\frac{f(x_k)}{f'(x_k)} xk+1=xk−f′(xk)f(xk)与前一步的近似值 x k x_k xk适当加权平均作为新的改进值: x k + 1 = λ x k + 1 ‾ + ( 1 − λ ) x k ( 0 < λ < = 1 ) x_{k+1} = \lambda\overline{x_k+1}+(1-\lambda)x_k(0<\lambda<=1) xk+1=λxk+1+(1−λ)xk(0<λ<=1)选择从 λ = 1 \lambda=1 λ=1开始,如果不满足这个上述附加条件,则将 λ \lambda λ减半,如此就能确保收敛性。
重根情形
设 f ( x ) = ( x − x ∗ ) m g ( x ) , g ( x ∗ ) ≠ 0 f(x)=(x-x^*)^mg(x),g(x^*)≠0 f(x)=(x−x∗)mg(x),g(x∗)̸=0,则 x ∗ x^* x∗为方程 f ( x ) = 0 f(x) = 0 f(x)=0的m重根,此时有: f ( x ∗ ) = f ′ ( x ∗ ) = ⋅ ⋅ ⋅ = f ( m − 1 ) ( x ∗ ) = 0 , f ( m ) ( x ∗ ) ≠ 0 f(x^*)=f'(x^*)=···=f^{(m-1)}(x^*)=0,f^{(m)}(x^*)≠0 f(x∗)=f′(x∗)=⋅⋅⋅=f(m−1)(x∗)=0,f(m)(x∗)̸=0
迭代函数 ϕ ( x ) = x − f ( x ) f ′ ( x ) \phi(x)=x-\frac{f(x)}{f'(x)} ϕ(x)=x−f′(x)f(x)的导数满足 ϕ ′ ( x ∗ ) = 1 − 1 m ≠ 0 \phi'(x^*)=1-\frac{1}{m}≠0 ϕ′(x∗)=1−m1̸=0,此时用牛顿法只是线性收敛,如果还想要平方收敛速度,就可以采用迭代法: x k + 1 = x k − m f ( x k ) f ′ ( x k ) x_{k+1}=x_k-m\frac{f(x_k)}{f'(x_k)} xk+1=xk−mf′(xk)f(xk)