中南大学自动化学院“智能控制与优化决策”课题组-第八章集成学习任务小结

1． 谈谈集成学习的概念和思想。

集成学习(ensemble learning)通过构建并结合多个学习器来完成学习任务，有时也被称为多分类器系统(multi-classifier system) 、基于委员会的学习(committee-based learning) 等. 集成学习的示意图如下所示：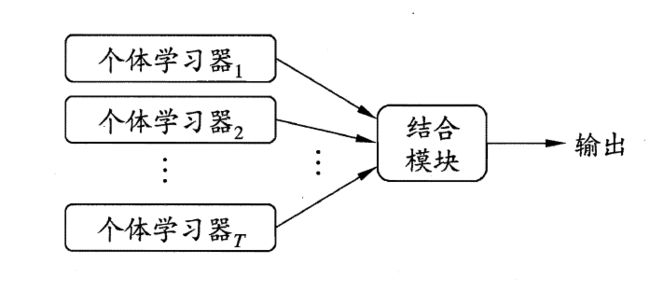
它的主要思想是通过将多个学习器进行结合，常可获得比单一学习器显著优越的泛化性能。由于基学习器的误差相互独立. 在现实任务中，个体学习器是为解决同一个问题训练出来的，它们显然不可能相互独立! 事实上，个体学习器的"准确性"和"多样性"本身就存在冲突. 一般的，准确性很高之后，要增加多样性就需牺牲准确性. 由于最终结果由各个学习器投票产生，因此，如何产生并结合"好而不同"的个体学习器，恰是集成学习研究的核心.

2． 集成学习方法可以分为哪几类，并且分别阐述它们的特点。

根据个体学习器的生成方式，目前的集成学习方法大致可分为两大类?即个体学习器问存在强依赖关系、必须串行生成的序列化方法? 以及个体学习器间不存在强依赖关系、可同时生成的并行化方法; 前者的代表是Boosting， 后者的代表是Bagging 和"随机森林" (Random Forest).

• Boosting方法
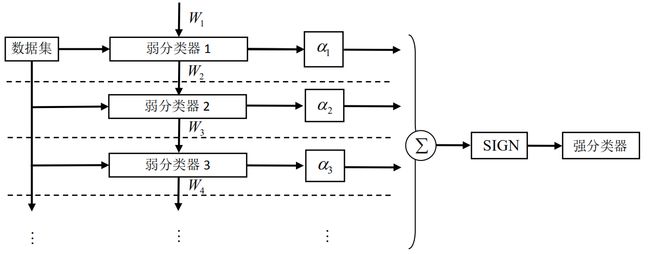
  先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本的分布进行调整，使得先前基学习器做错的训练样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器；如此重复进行，直至基学习器数目达到事先指定的值 $T$，最后将这 $T$ 个基学习器进行加权结合。流程图如下图所示：
  
  特点:每一轮训练都要检查当前生成的基学习器是否满足基本条件（如是否比随机猜测要好），若条件不满足，则当前学习器被抛弃，学习过程终止。若因学习轮数未达到$T$而导致效果不佳，可使用重采样法重新启动学习。
• Bagging
  这类方法是从初始训练数据集中采样出 $T$ 个含 $m$ 个训练样本的采样集，然后基于每个采样集训练出一个基学习器，再将这些基学习器根进行结合。该方法的流程图如下所示：
  
  特点：自助采样由于只使用了初始训练集的部分样本，而剩下的样本则可用作验证集来对泛化性能进行包外估计（在基学习器是决策树时可以辅助剪枝，当基学习器是神经网络时，可以减少过拟合的风险）。

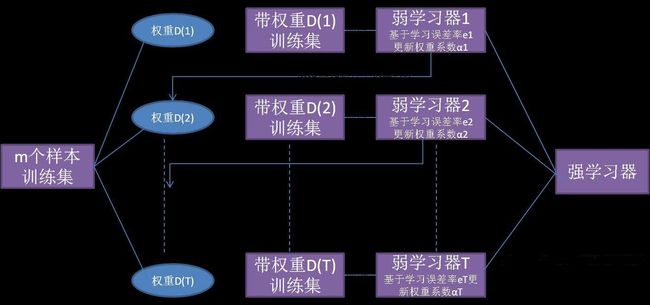
3． 在集成学习中，阐述针对二分类问题的AdaBoost算法实现过程。思考AdaBoost算法在每一轮如何改变训练数据的权值或概率分布?

3.1 Adaboost算法流程

迭代过程：
图解：

3.2主要步骤：

1.初始化训练数据的权值分布。

其中$D_1$表示第一次迭代每个样本的权值，$w_{11}$表示第一次迭代时第一个样本的权值，$N$为样本总数。
2.进行M次迭代
a）使用拥有权值分布$D_m(m=1,2,...,N)$的训练样本进行学习，得到弱分类器：$G_m(x):x\to$ {$-1,1$}.
弱分类器的性能指标通过以下误差函数的值${ϵ}_m$来衡量：

b)计算弱分类器$G_m$的话语权${\alpha }_m$(即是权值)，它表示$G_m$在最终分类器中的重要程度。计算方法如下：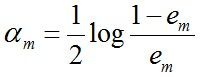
随着$e_m$减小，${\alpha }_m$逐渐增大。该式表明，误差率小的分类器在最终分类器中的重要程度大。
c）更新训练样本的权值分布，用于下一轮迭代，被错误分类的样本权值增加，被正确分类的样本权值减小。计算方法如下：


其中，$D_{m+1}$是用于下次迭代时的样本值，$w_{m+1，1}$是下一次迭代时，第$i$个样本的权值。$y_i$代表第$i$个样本对应的类别（1 或 -1），$G_m(x_i)$表示弱分类器对样本$x_i$的分类。若分类正确，则$G_m(x_i)$的值为1，反之为-1。其中$Z_m)$是归一化因子，计算方法如下：

第三步:组合弱分类器，获得强分类器
首先,对所有迭代过的分类器加权求和：
接着，将sign函数作用于求和结果，得到最终的强分类器$G(x)$:

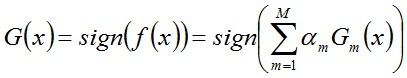
sign函数：是一个逻辑函数，用于判断实数的正负号。其定义为：

4．随机森林与集成学习之间有什么样的关系？

随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，而它的本质属于集成学习方法。
随机森林的名称中有两个关键词，一个是“随机”，一个就是“森林”。“森林”我们很好理解，一棵叫做树，那么成百上千棵就可以叫做森林了，这也是随机森林的主要思想–集成思想的体现。然而，bagging的代价是不用单棵决策树来做预测，具体哪个变量起到重要作用变得未知，所以bagging改进了预测准确率但损失了解释性。

学习完决策树后，了解决策树简单直观，易于理解，数据还不用预处理的同时对异常点容错率还异常的高。然而应用实际中，决策树容易过于拟合，性能不稳定，这就是需要集成来解决。理论依据是：大数定律，在试验不变的条件下，重复试验多次，随机事件的频率近似于它的概率。偶然中包含着某种必然。

集成是什么？类似于你随机问几千个人复杂的问题，然后汇总他们的答案，此时你会发现他们的答案比专家更为详细、精准。在机器学习里面，我们都是利用某一中估算器训练模型，现在聚合多个估算器去训练拟合数据，我们成为集成学习，这种方法称为集成方法。随机森林就是集成学习的产物，是由一组决策树构成的，每棵树基于训练集中不同的三分之二随机子集进行训练，每棵树的生长不再是基于最好的特征，随机森林在树的生长上引入了更多的随机性，而是在一个随机生成的特征子集中选择最好的特征，这样随机森林用更高的偏差换取更低的方差。这样的话，随机森林也不会像决策树重要的特征出现在跟节点附近，不重要的特征出现在叶节点未知。对于随机森林我们需要计算一个特征在所有决策树上的平均深度去估算 特征的重要性（特征在很多方面能够得到应用,例如在银行贷款业务中能否正确的评估一个企业的信用度,关系到是否能够有效地回收贷款。但是信用评估模型的数据特征有很多,其中不乏有很多噪音,所以需要计算出每一个特征的重要性并对这些特征进行一个排序,进而可以从所有特征中选择出重要性靠前的特征）。这一点是随机森林的重要特点，应用于特征选择。最后只要统计每棵树的结果就可以得出相应的结论。

5. 用python实现基于单层决策树的AdaBoost算法。

代码：

// An highlighted block
var foo ='bar'';

# -*- coding: utf-8 -*-

import numpy as np

def loadSimData():
    '''
    输入：无
    功能：提供一个两个特征的数据集
    输出：带有标签的数据集
    '''
    datMat = np.matrix([[1. ,2.1],[2. , 1.1],[1.3 ,1.],[1. ,1.],[2. ,1.]])
    classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
    return datMat, classLabels

def stumpClassify(dataMatrix,dimen,thresholdValue,thresholdIneq):
    '''
    输入：数据矩阵，特征维数，某一特征的分类阈值，分类不等号
    功能：输出决策树桩标签
    输出：标签
    '''
    returnArray =  np.ones((np.shape(dataMatrix)[0],1))
    if thresholdIneq == 'lt':
        returnArray[dataMatrix[:,dimen] <= thresholdValue] = -1
    else:
        returnArray[dataMatrix[:,dimen] > thresholdValue] = -1
    return returnArray

def buildStump(dataArray,classLabels,D):
    '''
    输入：数据矩阵，对应的真实类别标签，特征的权值分布
    功能：在数据集上，找到加权错误率（分类错误率）最小的单层决策树，显然，该指标函数与权重向量有密切关系
    输出：最佳树桩（特征，分类特征阈值，不等号方向），最小加权错误率，该权值向量D下的分类标签估计值
    '''
    dataMatrix = np.mat(dataArray); labelMat = np.mat(classLabels).T
    m,n = np.shape(dataMatrix)
    stepNum = 10.0; bestStump = {}; bestClassEst = np.mat(np.zeros((m,1)))
    minError = np.inf
    for i in range(n):
        rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max()
        stepSize = (rangeMax - rangeMin)/stepNum
        for j in range(-1, int(stepNum)+1):
            for thresholdIneq in ['lt', 'gt']:
                thresholdValue =  rangeMin + float(j) * stepSize
                predictClass = stumpClassify(dataMatrix,i,thresholdValue,thresholdIneq)
                errArray =  np.mat(np.ones((m,1)))
                errArray[predictClass == labelMat] = 0
                weightError = D.T * errArray
                #print "split: dim %d, thresh: %.2f,threIneq:%s,weghtError %.3F" %(i,thresholdValue,thresholdIneq,weightError)
                if weightError < minError:
                    minError = weightError
                    bestClassEst = predictClass.copy()
                    bestStump['dimen'] = i
                    bestStump['thresholdValue'] = thresholdValue
                    bestStump['thresholdIneq'] = thresholdIneq
    return bestClassEst, minError, bestStump

def adaBoostTrainDS(dataArray,classLabels,numIt=40):
    '''
    输入：数据集，标签向量，最大迭代次数
    功能：创建adaboost加法模型
    输出：多个弱分类器的数组
    '''
    weakClass = []#定义弱分类数组，保存每个基本分类器bestStump
    m,n = np.shape(dataArray)
    D = np.mat(np.ones((m,1))/m)
    aggClassEst = np.mat(np.zeros((m,1)))
    for i in range(numIt):
        print ("i:",i)
        bestClassEst, minError, bestStump = buildStump(dataArray,classLabels,D)#step1:找到最佳的单层决策树
        print ("D.T:", D.T)
        alpha = float(0.5*np.log((1-minError)/max(minError,1e-16)))#step2: 更新alpha
        print ("alpha:",alpha)
        bestStump['alpha'] = alpha
        weakClass.append(bestStump)#step3:将基本分类器添加到弱分类的数组中
        print ("classEst:",bestClassEst)
        expon = np.multiply(-1*alpha*np.mat(classLabels).T,bestClassEst)
        D = np.multiply(D, np.exp(expon))
        D = D/D.sum()#step4:更新权重，该式是让D服从概率分布
        aggClassEst += alpha*bestClassEst#steo5:更新累计类别估计值
        print ("aggClassEst:",aggClassEst.T)
        print (np.sign(aggClassEst) != np.mat(classLabels).T)
        aggError = np.multiply(np.sign(aggClassEst) != np.mat(classLabels).T,np.ones((m,1)))
        print ("aggError",aggError)
        aggErrorRate = aggError.sum()/m
        print ("total error:",aggErrorRate)
        if aggErrorRate == 0.0: break
    return weakClass

def adaTestClassify(dataToClassify,weakClass):
    dataMatrix = np.mat(dataToClassify)        
    m =np.shape(dataMatrix)[0]
    aggClassEst = np.mat(np.zeros((m,1)))
    for i in range(len(weakClass)):
        classEst = stumpClassify(dataToClassify,weakClass[i]['dimen'],weakClass[i]['thresholdValue']\
                                 ,weakClass[i]['thresholdIneq'])
        aggClassEst += weakClass[i]['alpha'] * classEst
        print (aggClassEst)
    return np.sign(aggClassEst)
if __name__  ==  '__main__':
    D =np.mat(np.ones((5,1))/5)
    dataMatrix ,classLabels= loadSimData()
    bestClassEst, minError, bestStump = buildStump(dataMatrix,classLabels,D)
    weakClass = adaBoostTrainDS(dataMatrix,classLabels,9)            
    testClass = adaTestClassify(np.mat([0,0]),weakClass)

结果：

// An highlighted block
i: 0
D.T: [[0.2 0.2 0.2 0.2 0.2]]
alpha: 0.6931471805599453
classEst: [[-1.]
 [ 1.]
 [-1.]
 [-1.]
 [ 1.]]
aggClassEst: [[-0.69314718  0.69314718 -0.69314718 -0.69314718  0.69314718]]
[[ True]
 [False]
 [False]
 [False]
 [False]]
aggError [[1.]
 [0.]
 [0.]
 [0.]
 [0.]]
total error: 0.2
i: 1
D.T: [[0.5   0.125 0.125 0.125 0.125]]
alpha: 0.9729550745276565
classEst: [[ 1.]
 [ 1.]
 [-1.]
 [-1.]
 [-1.]]
aggClassEst: [[ 0.27980789  1.66610226 -1.66610226 -1.66610226 -0.27980789]]
[[False]
 [False]
 [False]
 [False]
 [ True]]
aggError [[0.]
 [0.]
 [0.]
 [0.]
 [1.]]
total error: 0.2
i: 2
D.T: [[0.28571429 0.07142857 0.07142857 0.07142857 0.5       ]]
alpha: 0.8958797346140273
classEst: [[1.]
 [1.]
 [1.]
 [1.]
 [1.]]
aggClassEst: [[ 1.17568763  2.56198199 -0.77022252 -0.77022252  0.61607184]]
[[False]
 [False]
 [False]
 [False]
 [False]]
aggError [[0.]
 [0.]
 [0.]
 [0.]
 [0.]]
total error: 0.0
[[-0.69314718]]
[[-1.66610226]]
[[-2.56198199]]