LeetCode -- 877.石子游戏(解决博弈问题的动态规划通用思路) java
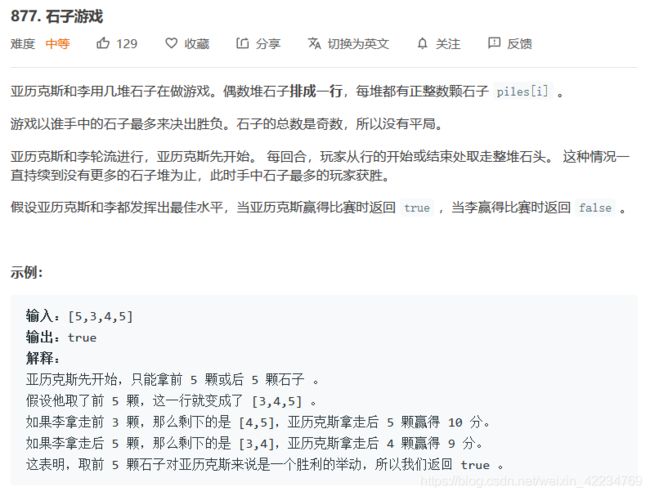

亚里克斯先开始,他赢返回true。
都最佳水平。
石子有偶数堆,奇数个。
此题堆数是偶数先手必胜,return true即可。
来自作者labuladong, 侵删。
解决博弈问题的动态规划通用思路:
博弈类问题的套路都差不多,下文举例讲解,其核心思路是在二维 dpdpdp 的基础上使用元组分别存储两个人的博弈结果。掌握了这个技巧以后,别人再问你什么俩海盗分宝石,俩人拿硬币的问题,你就告诉别人:我懒得想,直接给你写个算法算一下得了。
博弈问题的前提一般都是在两个聪明人之间进行,编程描述这种游戏的一般方法是二维 dp 数组,数组中通过元组分别表示两人的最优决策。博弈问题的前提一般都是在两个聪明人之间进行,编程描述这种游戏的一般方法是二维 dp 数组,数组中通过元组分别表示两人的最优决策。
之所以这样设计,是因为先手在做出选择之后,就成了后手,后手在对方做完选择之后,就变成了先手。这种角色转换使得我们可以重用之前的结果,是典型的动态规划标志。



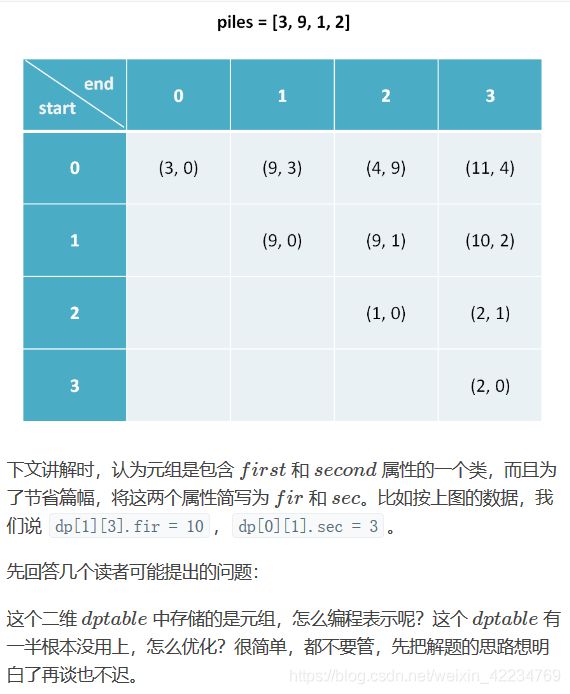
以下是对 dp 数组含义的解释:
dp[i][j].fir 表示,对于 piles[i...j] 这部分石头堆,先手能获得的最高分数。
dp[i][j].sec 表示,对于 piles[i...j] 这部分石头堆,后手能获得的最高分数。
举例理解一下,假设 piles = [3, 9, 1, 2],索引从 0 开始
dp[0][1].fir = 9 意味着:面对石头堆 [3, 9],先手最终能够获得 9 分。
dp[1][3].sec = 2 意味着:面对石头堆 [9, 1, 2],后手最终能够获得 2 分。
dp[i][j][fir or sec]
其中:
0 <= i < piles.length
i <= j < piles.length
对于这个问题的每个状态,可以做的选择有两个:选择最左边的那堆石头,或者选择最右边的那堆石头。 我们可以这样穷举所有状态:
n = piles.length
for 0 <= i < n:
for j <= i < n:
for who in {fir, sec}:
dp[i][j][who] = max(left, right)
# 解释:我作为先手,面对 piles[i...j] 时,有两种选择:
# 要么我选择最左边的那一堆石头,然后面对 piles[i+1...j]
# 但是此时轮到对方,相当于我变成了后手,要两步之和最大;
# 要么我选择最右边的那一堆石头,然后面对 piles[i...j-1]
# 但是此时轮到对方,相当于我变成了后手。
dp[i][j].fir = max(piles[i]+dp[i+1][j].sec, piles[j]+dp[i][j-1].sec)
#dp[i][j].fir = max( 选择最左边的石头堆 , 选择最右边的石头堆 )
# 解释:我作为后手,要等先手先选择,有两种情况:
# 如果先手选择了最左边那堆,给我剩下了 piles[i+1...j]
# 此时轮到我,我变成了先手;
# 如果先手选择了最右边那堆,给我剩下了 piles[i...j-1]
# 此时轮到我,我变成了先手。
if 先手选择左边:
dp[i][j].sec = dp[i+1][j].fir
if 先手选择右边:
dp[i][j].sec = dp[i][j-1].fir
根据 dp数组的定义,我们也可以找出 base case,也就是最简单的情况:
dp[i][j].fir = piles[i]
dp[i][j].sec = 0
其中 0 <= i == j < n
# 解释:i 和 j 相等就是说面前只有一堆石头 piles[i]
# 那么显然先手的得分为 piles[i]
# 后手没有石头拿了,得分为 0
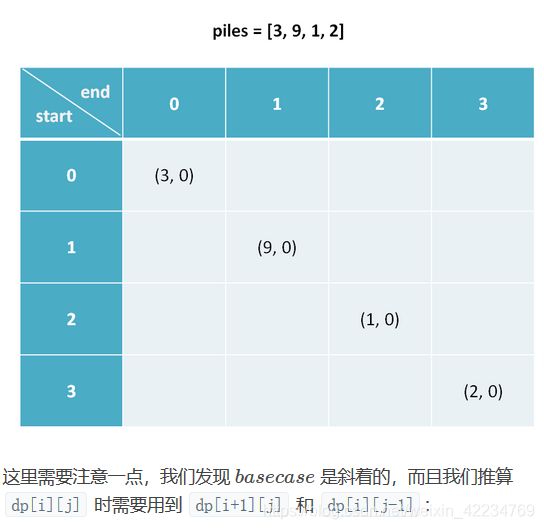
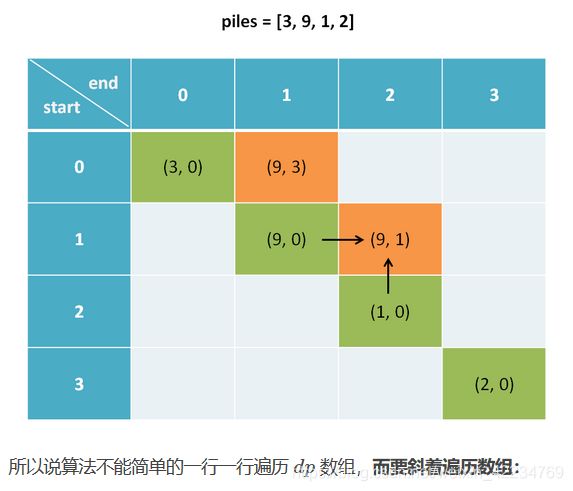
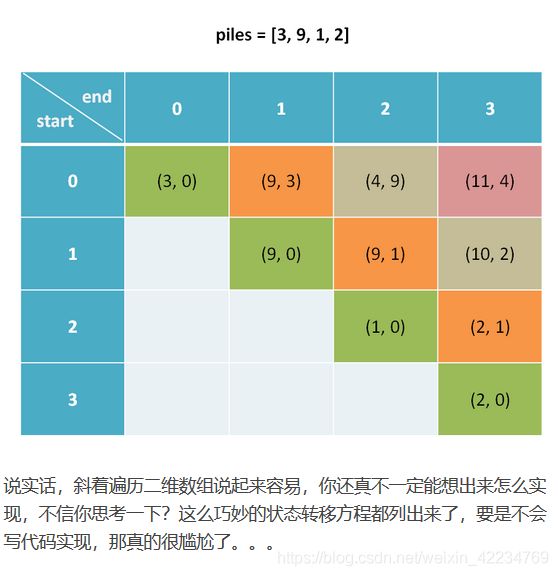
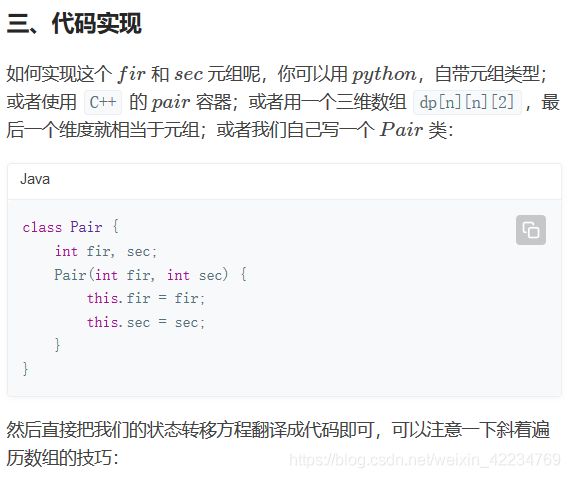
然后直接把我们的状态转移方程翻译成代码即可,可以注意一下斜着遍历数组的技巧:
/* 返回游戏最后先手和后手的得分之差 */
int stoneGame(int[] piles) {
int n = piles.length;
// 初始化 dp 数组
Pair[][] dp = new Pair[n][n];
for (int i = 0; i < n; i++)
for (int j = i; j < n; j++)
dp[i][j] = new Pair(0, 0);
// 动态规划的base case:ij相等,即只有一堆石头,先手选择
for (int i = 0; i < n; i++) {
dp[i][i].fir = piles[i];
dp[i][i].sec = 0;
}
// 动态转移:
// 斜着遍历数组
for (int l = 2; l <= n; l++) {
for (int i = 0; i <= n - l; i++) { // 行是0~n-1
int j = l + i - 1; // 列是行+1, 还需要加
// 状态转移方程:对dp[i, j]
int left = piles[i] + dp[i+1][j].sec;
int right = piles[j] + dp[i][j-1].sec;
// 套用状态转移方程:
if (left > right) {
dp[i][j].fir = left;
dp[i][j].sec = dp[i+1][j].fir;
} else {
dp[i][j].fir = right;
dp[i][j].sec = dp[i][j-1].fir;
}
}
}
Pair res = dp[0][n-1];
return res.fir - res.sec;
}



