【C++ 枚举问题入门】两个难度规模,N从20 -> 40
C++ 枚举问题入门
- Easy 规模,N=20
- 方法1:二进制枚举
- 例题 Petr and a Combination Lock
- 方法2:dfs枚举
- Hard 规模,N=40
- 例题:Circuit Counting
【枚举问题】
指的是 从N个数(或者元素)中,选择k个(k可以是指定,也可以是任意,0
求这样的 方案数,我们把这类问题叫做枚举问题。
Easy 规模,N=20
因为220 = 1 048 576 ,所以O(2N) 的复杂度规模可行!
方法1:二进制枚举
优点:对于不同题目写法差不多,好懂,新手友好向。
缺点:代码复杂,容易写错。
\ 原理 /
我们要从N个数字选择k个,那我们可以类比到二进制中去。
比如当N=3时,所有的二进制排列方案为:
如果我们看第i位,如果val[i]=1则表示我们选择i号元素;为0我们则不选
000 都不选
001 选择第三个元素
010 选择第二个元素
011 选择第二、第三个元素
100 选择第一个元素
101 选择第一、第三个元素
110 选择第一、第二个元素
111 都选
可以看到,十进制从0到2N-1 我们就把所有可能的情况都列举起来了。
例题 Petr and a Combination Lock
Petr has just bought a new car. He’s just arrived at the most known Petersburg’s petrol station to refuel it when he suddenly discovered that the petrol tank is secured with a combination lock! The lock has a scale of 360 degrees and a pointer which initially points at zero:
Petr called his car dealer, who instructed him to rotate the lock’s wheel exactly n times. The ii-th rotation should be ai degrees, either clockwise or counterclockwise, and after all n rotations the pointer should again point at zero.
This confused Petr a little bit as he isn’t sure which rotations should be done clockwise and which should be done counterclockwise. As there are many possible ways of rotating the lock, help him and find out whether there exists at least one, such that after all n rotations the pointer will point at zero again.
翻译:
n次已给操作度数,问你能否选择每次操作是顺时针或者逆时针,使得一开始指向0度的指针最后也会指向0度(一圈360度),只需输出YES or NO
思路:
我们二进制枚举,设每位1为顺时针旋转,0为逆时针旋转,二进制枚举即可
(代码为几个月前写的,有很多拙劣的地方hh)
#include
{
ans=0;
//cout << "cnt is " << cnt << " ";
now=i;
for(j=0;j<n;j++)///枚举每一位
{
//cout << now%2 << " ";
if(now%2)ans+=a[j];///当前位为1,顺时针
else ans-=a[j]; ///当前位为0,逆时针
if(ans<0)ans+=360; ///转过一圈了的话要重新调整一下度数
ans%=360;
now/=2; //计算now的下一位
}
if(ans==0) //ans=0表示有符合条件
{
pd=1;
break;
}
//cout << endl;
}
if(pd)cout << "YES";
else cout << "NO";
return 0;
}
方法2:dfs枚举
这里之前的博客已经多次提到啦!参考这篇,写的很详细!
DFS 排列与组合的简单搜索.
Hard 规模,N=40
今天遇到了一题规模比较大的题目。
首先思考一下为什么之前的方法不能用吧!
O(2n)=O(240)=1 099 511 627 776 >1e12
这计算结果得算到明年了!。
简单的思路:
我之前在某挑战程序设计竞赛书上看到过一题二分搜索
(不全是binary_search的那个二分搜索)
N个数选择4个,使得四个和为k。四重循环明显复杂度为O(N4)
如果N个中选择四个的话,我们可以先枚举其中选择两个的,再利用二分搜索,把O(N4)降到了O(N2logN)
例题:Circuit Counting
链接:
Circuit Counting.
题意:
有N个不相同的向量(没有0向量)。
选择其中的k个(0
(N<=40)
思路:
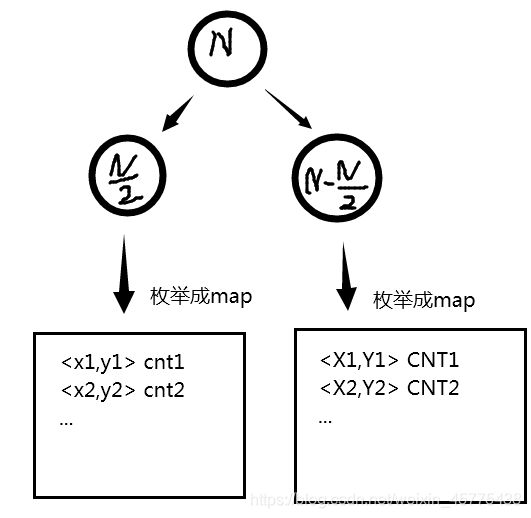
我先试着把N个元素分为两堆。(二分)
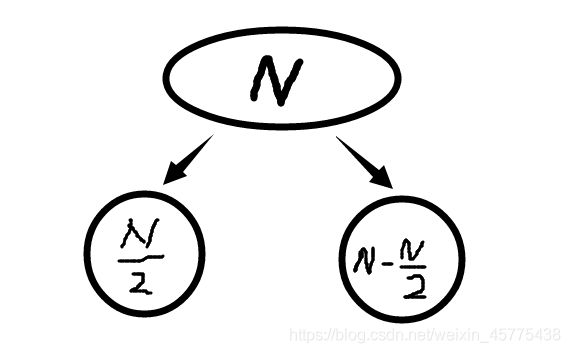
这样,前面的N/2个元素和后面的N-N/2个元素都是可以二进制枚举的。
每次选择好其中的几个元素之后,我们需要把这几个向量的和存储起来。这里我选择使用很方便的map映射
这里的代码不是很困难:
map<pair<int,int> ,ll>M1; ///表示的和向量枚举的方案数有k个
map<pair<int,int> ,ll>M2;
int pos=n/2;
int all = (1<<(pos));
for(int i=0;i<all;++i){ ///枚举前一半
int t=i;
int xx=0,yy=0;
for(int j=1;j<=pos;++j){
if(t&1==1){
xx+=aa[j];
yy+=bb[j];
}
t/=2;
}
///show(xx);show(yy);
M1[make_pair(xx,yy)]++;
///show(M1[make_pair(xx,yy)]);
}
all = (1<<(n-pos));
for(int i=1;i<all;++i){ ///枚举后一半
int t=i;
int xx=0,yy=0;
for(int j=1;j<=n-pos;++j){
if(t&1==1){
xx+=aa[pos+j];
yy+=bb[pos+j];
}
t/=2;
}
///show(xx);show(yy);
M2[make_pair(xx,yy)]++;
///show(M2[make_pair(xx,yy)]);
}
接下来怎么得出答案呢?
首先,我们可以简单地想到,选取某些向量使得向量和为0向量,这些向量分布有三种情况:
1. 都在A堆中枚举过了
2. 都在B堆中枚举过了
3. A堆中有几个,B堆中有几个
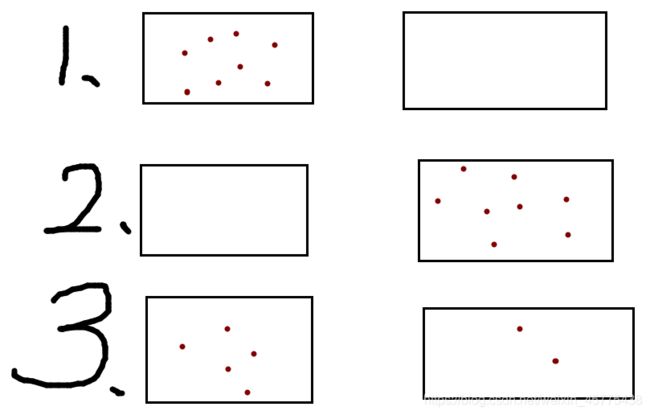
而一和二的情况很简单,答案就是两个堆中<0,0>的数量和就行了。
关键是如果两个堆中都有的点怎么选择呢?
如果堆A中
那么我们的答案很明显就是需要增加c1 * c2 (全排列方案数)
然后我们再进行化简修改一下。因为原题没有0向量,我们在A堆中额外增加一个0向量,那么最终答案为以下相加:(搜索)
1. map1 中<0,0>的cnt -1 (我们增加了一个0向量,减去它!)
2. map1
【为什么省略了一种情况嘞?】
情况1是只选择堆1的
情况2中去除x=0 , y=0的点,
情况2中,如果x=0 , y=0 ,那么表示有两种:
【一种是两个堆都选择的,但是两个堆中选择的向量和都为0向量】
【一种是只选择堆2的点,堆一选择了我们额外插入的0向量】
很晕?细品!
代码复杂度O(2N/2 *logN)
AC代码:
#include