服务计算第4周:用go维护一个最小堆
课程网址:服务计算 - 云应用开发方法、技术与架构
项目传送门: week-4
环境:win10, vscode
文章目录
- 1. 作业要求
- 2. 堆、二叉树等基础数据结构
- 2.1 完全二叉树
- 2.2 堆
- 2.3 结构性和堆序性
- 2.4 最大堆和最小堆
- 3. 堆排序算法
- 4. 最小堆实现
- 4.1 数据结构
- 4.1 初始化最小堆
- 4.2 增加元素
- 4.3 删除元素
- 4.4 总结
- 4.5 所有代码如下
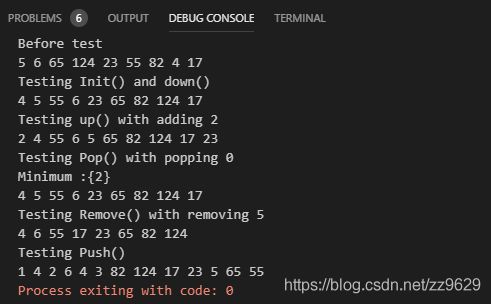
- 4.6 实验结果
- 5. 参考资料
- 6. 总结
1. 作业要求
2. 堆、二叉树等基础数据结构
由于数据结构学的不太好,参考了 排序方法(五)堆排序
这里整理一下我学到的东西,方便以后复习。
这里的内容90%来自这篇博客。
2.1 完全二叉树
完全二叉树是增加了限定条件的二叉树。假设一个二叉树的深度为n。为了满足完全二叉树的要求,该二叉树的前n-1层必须填满,第n层也必须按照从左到右的顺序被填满,比如下图:
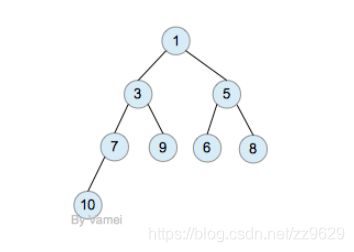
2.2 堆
(最小堆/最小堆的原理相同)
堆的一个经典的实现是完全二叉树(complete binary tree)。这样实现的堆成为二叉堆(binary heap)。
本篇博客讲的堆就是按顺序存储的完全二叉树。
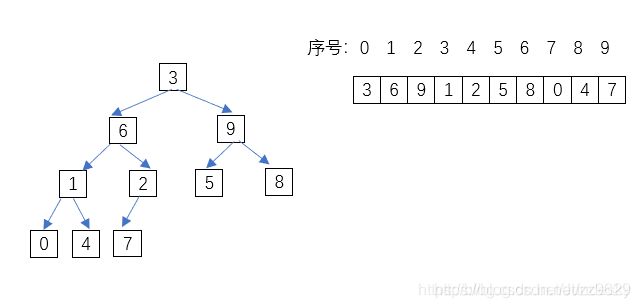
2.3 结构性和堆序性
这很重要,因为我们在实现堆的函数操作时,需要利用一个index求出这个节点的父节点以及左右孩子节点。
- 结构性:二叉堆是一颗完全二叉树,完全二叉树可以用一个数组表示,不需要指针,所以效率更高。当用数组表示时,数组中任一位置
i上的元素,其左儿子在位置2i+1上,右儿子在位置2i + 2上,其父节点在位置i / 2 - 1(n/2向下取整)上。
如6的序号为1;
那么它的左孩子序号为3,值为1;
右孩子序号为4,值为2;
父节点序号为(1-1)/ 2 =0,值为3 - 堆序性质:堆的最小值或最大值在根节点上,所以可以快速找到最大值或最小值。
最后一个有孩子的结点序号为n/2-1(n/2向下取整),其中n为元素个数;它前面的所有结点都有孩子;比如上图,最后一个有孩子的结点序号为:10/2-1 = 4。
2.4 最大堆和最小堆
最大堆和最小堆是二叉堆的两种形式。
最大堆:根结点的键值是所有堆结点键值中最大者的堆。
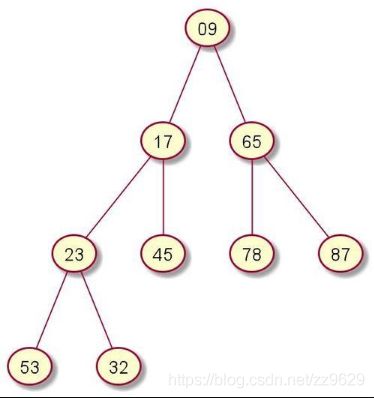
最小堆:根结点的键值是所有堆结点键值中最小者的堆。
最小堆如下:
3. 堆排序算法
接下来可以开始进入正题了。以从小到大排序为例,堆排序的基本思想是:
(1)把数据按顺序填入堆;
(2)构造大根堆(原因见下文);具体步骤为:
- 从
最后一个有孩子的结点开始,向前遍历所有结点; - 对于一个结点k,若k的值小于孩子的值,交换k和值最大的孩子的位置;交换完成后,一定注意检查k与新孩子是否满足大根堆;
- 遍历完成,就形成了初始大根堆。
(3)第一个元素现在是值最大的。交换第一个元素和最后一个元素的位置。交换完成后,最大的元素就固定在数组末尾。不管最后一个元素,将前面的所有元素再次构造大根堆,重复执行本步骤,直到构造的大根堆只剩一个元素,排序就完成了。
仍然以上图为例子:
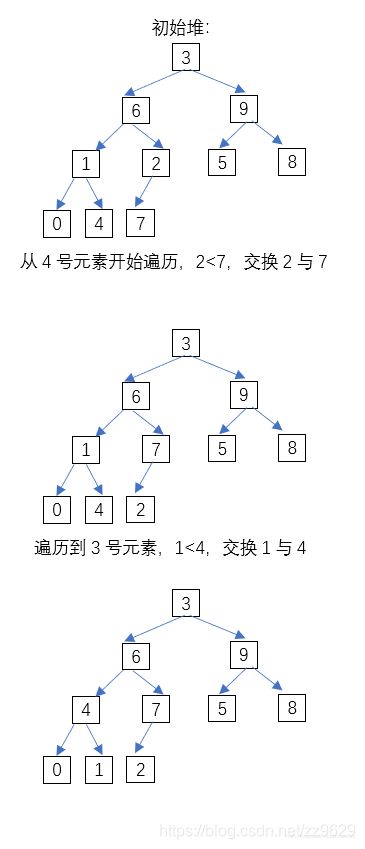 |
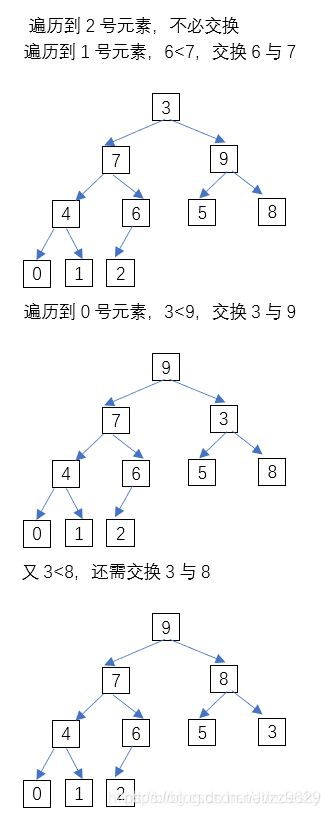 |
|---|
这样初始大根堆就构造完毕了。接下来,交换9和2的位置,忽略9建立大根堆:
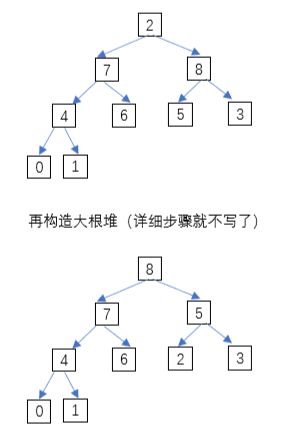 |
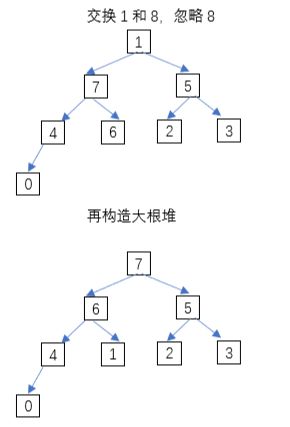 |
|---|---|
后续步骤不再详细描述。 注:构建大根堆的原因是,可以将最大的元素排到后面,即实现从小到大排序。所以,如果要从大到小排序,就用小根堆。
4. 最小堆实现
作业要求仅仅是实现一个最小堆,并没有要求排序。
要先实现最小堆才能进行排序。
因此我们要先实现一个最小堆,仅仅是保证最小节点是堆顶。也就是前面堆排序算法中所涉及到的初始堆。不过例子用的是最大堆,代码中所实现的是最小堆,原理都一样。
4.1 数据结构
这里用到的是结构体Node.
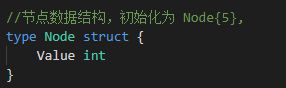
主函数中,创建一个node的数组,初始化如下,并用自己写的函数display输出。
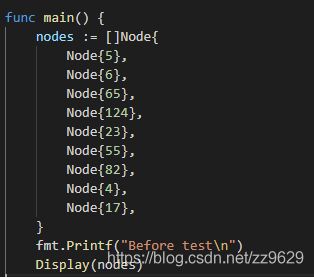
堆的遍历输出 (PS: 这个实现其实是有问题的,因为我们的node结构体只有一个int类型素以可以直接输出,关于结构体的数据输出,我把这个搞完再研究研究。
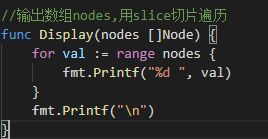
4.1 初始化最小堆
init()
init()函数用于一个堆的初始化,也就是将一个无须的数组整合成一个最小堆,仅仅是将最小元素放在了堆顶。
仅仅是初步的整合,因此直接从有最后一个有孩子的节点开始,也就是i / 2 - 1
向前遍历所有的节点。均用到了down函数。
- 调用
down函数,需要down(下沉)的元素在切片中的索引为i,n为heap的长度,将该元素下沉到该元素对应的子树合适的位置,从而满足该子树为最小堆的要求。
4.2 增加元素
push()
push()函数包括append() 和 up()两个过程。
调用append()函数,即可增加新元素,这个时候的新元素位于数组的末端,因此需要将这个新元素上浮,调整至合适的位置,调用up()函数;
4.3 删除元素
pop() 函数弹出最小元素,remove(带参数)弹出指定数据
pop()
- 先把最小的元素也就是序号为0的节点放到最后,和最后一个元素交换数据。
- 然后维护长度减一的堆(0~n-1),也就是把新的堆首元素down下沉,维护顺序。
- 最后一个元素才是最小的,需要输出的数据
remove()
其实原理相同,只不过pop()弹出的节点的序号是0,用down维护堆时调用的参数从0开始,remove()需要遍历数组找到数据,弹出节点的序号为index,维护堆时调用的参数从index开始即可。
4.4 总结
其实up和down都只是中间调用的辅助函数,如果要编写一个类的话,大概pop/push/remove都是外部可调用的函数,而up/down都是类的私有函数。不过go语言是面向过过程的,目前我还不知道怎么封装函数。
4.5 所有代码如下
package main
import (
"fmt"
// "reflect"
)
//输出数组nodes,用slice切片遍历.node结构体只有一个int数据,所以可以直接输出
func Display(nodes []Node) {
for val := range nodes {
fmt.Printf("%d ", val)
}/*
//对于每一个node结构,输出其不同成员
for i := range nodes {
val := reflect.ValueOf(i)
for j := 0; j < val.NumField(); j++ {
fmt.Printf("%v ", val.Field(j))
}
}
*/
fmt.Printf("\n")
}
//节点数据结构,初始化为 Node{5},果果有两个成员变量,比如Node{5, "Jim"}
type Node struct {
Value int
}
/*
用于构建结构体切片为最小堆,需要调用down函数。
从最后一个有孩子的结点开始,向前遍历所有结点;
最后一个有孩子的结点序号为:n/2-1 ,n为元素个数
对于一个结点k,若k的值大于孩子的值,交换k和值最大的孩子的位置;
交换完成后,一定注意检查k与新孩子是否满足小根堆;
*/
func Init(nodes []Node) {
for i := len(nodes)/2 - 1; i >= 0; i-- {
down(nodes, i, len(nodes))
}
}
/*
需要down(下沉)的元素在切片中的索引为i,n为heap的长度,将该元素下沉到该元素对应的子树合适的位置,从而满足该子树为最小堆的要求
在这里完成该节点和他的孩子的大小比较
对于一个结点k,若k的值大于孩子的值,交换k和值最小的孩子的位置;
此时这个孩子的值放在了高处
而k成为孩子,这时有了新的孩子。继续比较。
到最后满足它的孩子都比他大的条件,交换完成后,一定注意检查k与新孩子是否满足小根堆;
*/
func down(nodes []Node, i, n int) {
parent := i
child := 2*parent + 1
temp := nodes[parent].Value
for {
if child < n {
//左右孩子中最小孩子为child
if child+1 < n && nodes[child].Value > nodes[child+1].Value {
child++
}
//temp比child还小,说明已经是最小值,停止。
if temp <= nodes[child].Value {
break
}
//temp比最小的孩子大,说明需要交换temp和值最小的孩子的位置。还要继续向下,比如9 > 5
//所以先把parent的值换成它的孩子中最小的值,将5放在上面,9放在下面继续沉
nodes[parent].Value = nodes[child].Value
//向下继续寻找,这时它已经是新的节点的父母,要维护以前的顺序,比如本来是5 78,但是现在是9 78,明显需要重排
parent = child
child = child*2 + 1
} else {
break
}
}
//最后找到一种稳定的次序,这时把最小的孩子赋值为之前的temp,也就是temp找到了自己的位置
nodes[parent].Value = temp
}
// 用于保证插入新元素(j为元素的索引,切片末尾插入,堆底插入)的结构体切片之后仍然是一个最小堆
//j的父节点为i,j = 2*i + 1 或者 j = 2*i + 2.因此i = (j-1)/2
func up(nodes []Node, j int) {
child := j
parent := (j - 1) / 2
for {
if child == 0 {
break
}
if nodes[parent].Value < nodes[child].Value {
break
}
//新插入的堆底元素比他的父节点小,因此要交换数据,并且继续向上维护,所以叫数据的上浮
temp := nodes[child].Value
nodes[child].Value = nodes[parent].Value
nodes[parent].Value = temp
child = parent
parent = (parent - 1) / 2
}
}
/*
弹出最小元素,并保证弹出后的结构体切片仍然是一个最小堆,第一个返回值是弹出的节点的信息,第二个参数是Pop操作后得到的新的结构体切片
先把最小的元素放到最后,和最后一个元素交换数据。
然后维护长度减一的堆,也就是把新的堆首元素down下沉,维护顺序。
最后一个元素才是最小的,需要输出的堆
*/
func Pop(nodes []Node) (Node, []Node) {
min := nodes[0]
//将堆顶元素换成堆底元素
nodes[0].Value = nodes[len(nodes)-1].Value
//切片,堆的长度--
nodes = nodes[:len(nodes)-1]
//维护新的堆,将堆顶元素下沉
down(nodes, 0, len(nodes)-1)
return min, nodes
}
/*
保证插入新元素时,结构体切片仍然是一个最小堆,需要调用up函数
调用append函数实现增加节点,然后up函数让数据上浮,重新排序维护最小堆
返回最后的node数组
*/
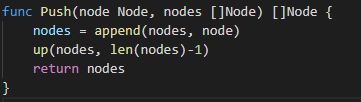
func Push(node Node, nodes []Node) []Node {
nodes = append(nodes, node)
up(nodes, len(nodes)-1)
return nodes
}
// Removing 移除切片中指定索引的元素,保证移除后结构体切片仍然是一个最小堆
/*
和pop函数原理相同,只不过pop是要把堆顶元素放到末尾,remove需要把指定的元素放到末尾,然后对于新的值进行下沉
新的值必然大于他的父节点,所以不需要再从堆首往下维护,直接从i开始往下维护即可
*/
func Remove(nodes []Node, node Node) []Node {
for i := 0; i < len(nodes); i++ {
if node.Value == nodes[i].Value {
nodes[i].Value = nodes[len(nodes)-1].Value
nodes = nodes[0 : len(nodes)-1]
down(nodes, i, len(nodes)-1)
break
}
}
return nodes
}
func main() {
nodes := []Node{
Node{5},
Node{6},
Node{65},
Node{124},
Node{23},
Node{55},
Node{82},
Node{4},
Node{17},
}
fmt.Printf("Before test\n")
Display(nodes)
fmt.Printf("Testing Init() and down()\n")
Init(nodes)
Display(nodes)
fmt.Printf("Testing up() with adding 2\n")
add := Node{2}
nodes = append(nodes, add)
up(nodes, len(nodes)-1)
Display(nodes)
fmt.Printf("Testing Pop() with popping 0\n")
min, nodes := Pop(nodes)
fmt.Printf("Minimum :%d\n", min)
Display(nodes)
fmt.Printf("Testing Remove() with removing 5\n")
remove := Node{5}
nodes = Remove(nodes, remove)
Display(nodes)
fmt.Printf("Testing Push()\n")
node5 := Node{5}
node4 := Node{4}
node3 := Node{3}
node2 := Node{2}
node1 := Node{1}
nodes = Push(node5, nodes)
nodes = Push(node4, nodes)
nodes = Push(node3, nodes)
nodes = Push(node2, nodes)
nodes = Push(node1, nodes)
Display(nodes)
}
4.6 实验结果
5. 参考资料
尤其感谢go语言实现最小堆并测试这个博客,基础知识的图片写得很明白。代码也是参考了部分,但是自己添加了很多注释,并对remove和display函数做了改进。
- 最大堆和最小堆 golang实现
- Go语言中怎么实现一个小根堆
- 纸上谈兵: 堆 (heap)
- 如何遍历结构体
6. 总结
- 通过此次的编程学到了堆、堆排序、复习了数据结构的增删元素
- 堆排序并没有要求,但是我觉得算法如下:
- 在init函数初始化一个最小堆之后,将最小元素放到堆底
- 维护n-1数量的堆,继续选出最小元素,放到堆底
… - 最后可以实现从大到小的排序。
- 关于display函数显示一串结构体的元素
我的代码的确可以把节点的值显示出来,但是仅仅是因为这个结构体只有一个元素。如果有多个元素,比如node节点有两个元素(比如一个int,一个string)比如这样:
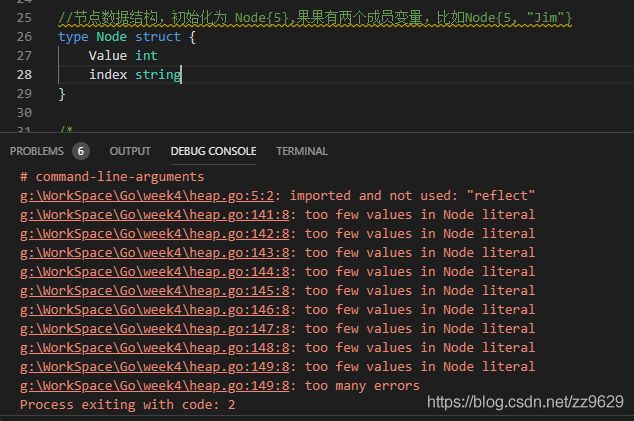
我在网上查询的方法是调用reflect库,但是我试着写了一下,会报错panic。
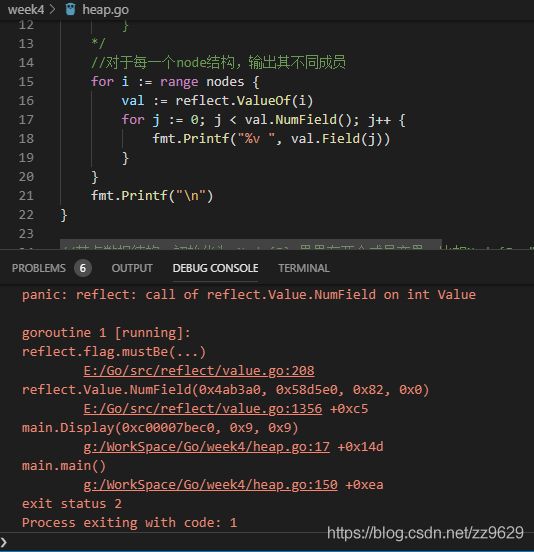
还未解决。
更新一下关于输出一串结构体的数据,这样可以输出Value成员的数据。
这个range切片应该是是单个的node结构体。原理我还没有搞清楚,以后再看看go的语法。
但是正确用法如下:
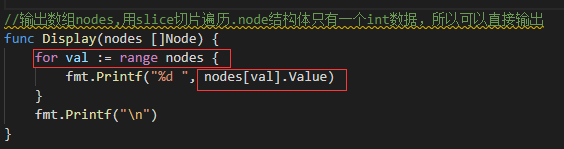
如果直接输出val的话,这个是节点的序号。输出会是这个样子:
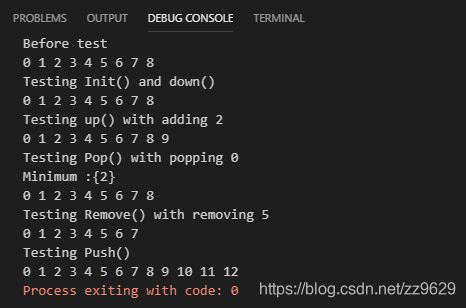
输出nodes[val].Value实验结果如下: