Focal Loss for Dense Object Detection整体介绍及部分细节讲解
目录
- 一、整体总结
- 二、Focal loss原理及推导
- 1. 多类别交叉熵
- 2. focal loss推导
- 2.1 平衡交叉熵
- 2.2 focal loss定义
- 三、 类别不平衡和模型初始化
- 四、RetinaNet检测器
- 1. 网络结构
- 2. 分类子网络
- 3. 候选框回归子网络
- 五、论文细节
一、整体总结
主要是针对类别不平衡设计了初始化和loss函数。
初始时将rare类的prior设置的比较低。
引入了alpha和gamma参数,分别用于平衡正负例和难易例。
设计了RetinaNet检测器来考察以上设置效果。
二、Focal loss原理及推导
1. 多类别交叉熵
给定两个概率分布:p(理想结果即正确标签向量)和q(神经网络输出结果即经过softmax转换后的结果向量),则通过q来表示p的交叉熵为:
H ( p , q ) = − ∑ x p ( x ) l o g q ( x ) H(p,q)=−∑_xp(x)logq(x) H(p,q)=−x∑p(x)logq(x)
注意:既然p和q都是一种概率分布,那么对于任意的x,应该属于[0,1]并且所有概率和为1
∀ x , p ( X = x ) ∈ [ 0 , 1 ] 且 ∑ x p ( X = x ) = 1 ∀x,p(X=x)\in[0,1]且∑_xp(X=x)=1 ∀x,p(X=x)∈[0,1]且x∑p(X=x)=1
交叉熵刻画的是通过概率分布q来表达概率分布p的困难程度,其中p是正确答案,q是预测值,也就是交叉熵值越小,两个概率分布越接近。
2. focal loss推导
在本篇论文中,所用的交叉熵公式是二分类的交叉熵,可以类比着上一节的多类别交叉熵进行查看。
C E ( p , y ) = { − l o g ( p ) y = 1 − l o g ( 1 − p ) o t h e r w i s e . CE(p, y)= \begin{cases} −log(p) & y =1\\ −log(1 − p) & otherwise. \end{cases} CE(p,y)={−log(p)−log(1−p)y=1otherwise.
其中 y ∈ { ± 1 } y \in\{±1\} y∈{±1}代表正确类别, p ∈ [ 0 , 1 ] p \in [0, 1] p∈[0,1]代表着模型预测出的y=1的概率。
为了公式的简洁,做如下定义。
p t = { p y = 1 1 − p o t h e r w i s e . p_t =\begin{cases} p& y =1\\ 1-p & otherwise. \end{cases} pt={p1−py=1otherwise.
这样上述的二分类交叉熵公式就可以表示为: C E ( p , y ) = C E ( p t ) = − l o g ( p t ) CE(p, y)=CE(p_t)=-log(p_t) CE(p,y)=CE(pt)=−log(pt)
然而这个loss有一个问题:即使有些例子能被很容易的归类( p t ≫ 0.5 p_t\gg 0.5 pt≫0.5),这些例子的loss也不是很小。当把很多的easy例的loss加起来的时候,这些小loss值可能会影响rare类的loss值。
2.1 平衡交叉熵
普遍使用的方式是引入权值参数 α ∈ [ 0 , 1 ] \alpha\in [0,1] α∈[0,1],类别1的loss乘上 α \alpha α,类别-1的loss乘上 1 − α 1-\alpha 1−α。实践中 α \alpha α可以被设置为类别频数的逆或者被当作超参数通过交叉验证得到。为了更好的表示,定义了 α t \alpha_t αt。
α t = { α y = 1 1 − α o t h e r w i s e . \alpha_t =\begin{cases} \alpha & y=1\\ 1-\alpha & otherwise. \end{cases} αt={α1−αy=1otherwise.
这样 α − b a l a n c e \alpha-balance α−balance的CE损失就可以表示为:
C E ( p t ) = − α t l o g ( p t ) CE(p_t)=-\alpha_t log(p_t) CE(pt)=−αtlog(pt)
2.2 focal loss定义
α − b a l a n c e \alpha-balance α−balance的CE损失在一定程度上处理了类别数量不平衡,但是其没有平衡easy例和hard例。也就是大量的概率高的easy例会占了loss中的大部分,从而主导了梯度。所以本文引入了参数来降低easy例的权重,从而更集中训练hard negatives.。
引入了调节参数 ( 1 − p t ) γ , γ ≥ 0 (1-p_t)^\gamma, \gamma\ge 0 (1−pt)γ,γ≥0。定义focal loss为:
F L ( p t ) = − ( 1 − p t ) γ l o g ( p t ) FL(p_t)=-(1-p_t)^\gamma log(p_t) FL(pt)=−(1−pt)γlog(pt)
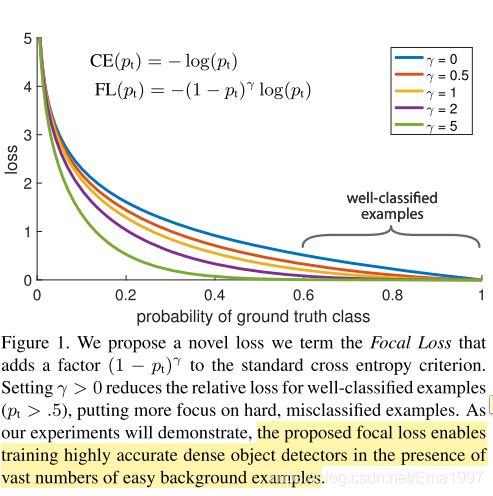
focal loss的可视化如图, γ \gamma γ使得被很好分类的实例的loss降低,从而能更加关注不好分类的实例的训练。当一个实例被误分类,那么其 p t p_t pt会很小,那么调节参数 ( 1 − p t ) γ (1-p_t)^\gamma (1−pt)γ接近于1,所以此时loss几乎不受影响。 γ \gamma γ很好的调节了easy例被降低权重的比例。(在实验中 γ = 2 \gamma=2 γ=2效果最好)
在实验中使用 α − b a l a n c e \alpha-balance α−balance的focal loss:
F L ( p t ) = − α t ( 1 − p t ) γ l o g ( p t ) FL(p_t)=-\alpha_t(1-p_t)^\gamma log(p_t) FL(pt)=−αt(1−pt)γlog(pt)
三、 类别不平衡和模型初始化
二分类模型默认被初始化为y=-1和1的类别有相同的初始概率。然而由于类别不平衡,整体的loss会被比较多的类别主导。所以引入了“prior”概念来表示在训练初始化时rare类的概率,用 π \pi π表示。初始时将rare类的 π \pi π设置的比较低。(此处我理解是将概率设置的比较低之后,loss就会相应变大,从而使得rare类更加主导训练过程。不是十分确定)
四、RetinaNet检测器
1. 网络结构
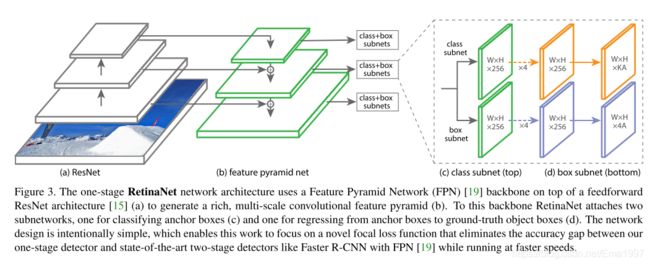
检测器的结构如图,由backbone网络和两个subnet组成,backbone用于得到特征图,两个自网络分别用于目标分类和候选框回归(矫正)。
其中backbone由ResNet+FPN组成。结构如下:

这个结构和Feature pyramid networks for object detection一文中有些不同,然而具体是哪里不同并不是此文的重点,所以不在此赘述。
在本文中,利用P3、P4、P5、P6、P7层得到的金字塔特征图,图中的C1到C5分别是ResNet的5个阶段的最后一层输出,圆圈之间进行的是2x上采样。(附录中有ResNet的网络结构,如果不理解C1到C5是什么,可以看一下那个网络结构。)每个金字塔层都有 C = 256 C=256 C=256个通道。
2. 分类子网络

每层的特征图(P3到P7)共享参数,但是和候选框回归网络不共享参数。在实验中设置通道数C=256,每个位置锚框数A=9,目标类别数K。
3. 候选框回归子网络
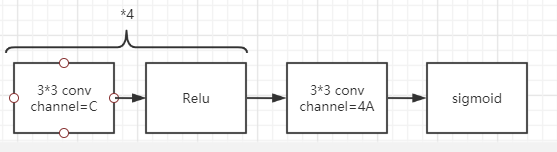
为每个位置的A=9个锚框生成4个回归结果,这部分和RCNN系列相似。如果想要了解原理可以看一文读懂Faster RCNN的2.4节bounding box regression原理。
五、论文细节
- γ \gamma γ越大,loss下降的越快。
- 提出的focal loss使得在有大量easy背景数据时,训练高准确度的密集物体检测器变成可能。
- 前景背景类的不平衡导致one-stage的效果差。
- 改进标准交叉熵损失函数,使其在比较好分类的例子上减低权重。
- 在RCNN系列中,类别不平衡被两阶段处理和样例选择解决(先提出候选框,再选出一定数量的ROI用于后续的检测网络训练与预测,其中正例与负例的比值可以在选择时固定,这样就很好的解决了类别不平衡的问题)。
- 2阶段的检测器(RCNN系列)能够通过减少输入图像resolution和proposal数量来提升速度。
- focal loss中设置了 α \alpha α超参数来平衡正负例loss, γ \gamma γ来平衡难/易例。
- imbalance带来的问题:
A. 训练不充分:大部分位置都是easy negatives(比较好分类的负例,如大量背景),这些例子没有贡献有用的学习信号。
B. easy negtives可能会影响训练,从而导致退化的模型。 - 常见的解决imbalance的方法是hard negative mining。
- 解决类别不平衡问题的robust loss减低error大的hard example的权值,而本文提出的focal loss减低easy example的权值。focal loss和robust loss的处理方式相反,focal loss更关注于在难例上的稀疏集上训练。
- p t p_t pt越大, ( 1 − p t ) (1-p_t) (1−pt)越小,从而使得 p t p_t pt大的在loss中占比变小。
- 两阶段的方法用pooling或align的方法可以归类任何位置、大小、比例的框,然而单阶段的方法只用了固定大小的grid,所以比较流行的方式是用不同的anchor来归类不同大小、比例、位置的框。
- 两阶段的方法,虽然可以归类不同类型框,但是由于饱和,所以效果不是特别明显。
- resolution为600pixel的RetinaNet的准确率和Faster RCNN持平,且更快。而如果图片尺寸更大,RetinaNet的效果会超过所有two-stage网络,同时还是很快。
- 锚框设置:
每层{1:2, 2:1, 1:1}的长宽比
每层加上size{ 2 0 , 2 1 3 , 2 2 3 2^0, 2^{\frac{1}{3}},2^{\frac{2}{3}} 20,231,232}的框(此处不是很理解,所以打算看看代码之后再确定什么意思)
所以每层共9个锚框,这些锚框的尺度从32 pixels到813 pixels。
为每一个锚框设置长度为K的one-hot检测向量,每个向量中只有一个位置是1,也就是只能被归为1类,其他位置都是0。 - 如果anchors与真值框的IoU大于等于0.5则为正例,如果[0, 0.4)则为背景类,也就是负例。如果IoU在[0.4, 0.5),那么训练时忽略该框。
- 为了提升速度,用0.05的阈值筛选出是前景的框,再再每个FPN层中选出分数最高的1000个预测进行处理。之后再将每一层的1000个预测合起来组成一个集合,再用阈值为0.5的non-maximum suppression(NMS,非极大值抑制)来产生最后的结果。
- γ = 2 \gamma=2 γ=2时效果好,鲁棒区间是 γ ∈ [ 0.5 , 5 ] \gamma\in [0.5, 5] γ∈[0.5,5]。
- 训练过程中focal loss应用于每张图的所有约等于100k个锚框上(与其他的只选一部分锚框进行loss计算的方法不同)。
- 一张图的整体focal loss: ∑ F L ( a n c h o r ) 真 值 锚 框 数 量 \frac{\sum{FL(anchor)}}{真值锚框数量} 真值锚框数量∑FL(anchor)
- α \alpha α要和 γ \gamma γ配套, γ \gamma γ越大, α \alpha α要适当降低, γ = 2 , α = 0.25 \gamma=2, \alpha=0.25 γ=2,α=0.25时效果最好。
- 初始化:
A. backbone选用ResNet-50-FPN和ResNet-101-FPN,这两个模型的参数用预训练的ImageNet1k参数初始化
B. FPN模型的初始化和Feature pyramid networks for object detection一文中相同。
C. 两个子网络中,除了最后一层之外的其他层用 σ = 0.01 \sigma=0.01 σ=0.01的高斯权值初始化,bias b=0。
D. 分类子网络的最后一层的 b = − l o g ( ( 1 − π ) / π ) b=-log((1-\pi)/\pi) b=−log((1−π)/π),使得训练初所有anchor以约等于 π \pi π的confidence被标记为前景类。 π \pi π设置为0.01。

- 优化:
A. SGD,weight decay=0.0001,momentum=0.9
B. 每个GPU训练两张图,共8个GPU。
C. lr:0.01(60k)→0.001(20k)→0.0001(10k)总共90k iter
D. 数据增强采用了水平的翻转
E. 训 练 l o s s = ∑ F L + L 1 训练loss=\sum{FL}+L_1 训练loss=∑FL+L1,其中 L 1 L_1 L1是候选框回归的loss。
F. 模型的训练时间大概10到35小时。 - 实验:
A. 训练:COCO trainval35k
B. 损害和准确率(lesion & sensitivity)研究:minival
C. 主要结果显示:test-dev(测评服务器上的)
参考:
- https://www.cnblogs.com/always-fight/p/10370412.html
- https://www.jianshu.com/p/596e4171f7ad