机器学习入门介绍

1. 机器学习介绍

1.1 基本术语

机器学习：利用经验、通过计算、构建模型，来改善系统自身的性能。
属性（特征）：描述事物在特定方面的表现或性质的事项。
属性值：属性上的取值。
属性空间（输入空间）：属性的所有可能取值构成的集合，若属性为多维特征则是由多维属性张成的空间，属性空间$\mathcal{X}$。

记录（样本、实例）：一个具体事物的属性描述，由属性向量表示。

例如：第$j$个记录${\mathbf{x}}_j$的属性向量，表示如下
$${\mathbf{x}}_j={\left(x_j^{(1)},x_j^{(2)},\cdots ,x_j^{(i)},\cdots ,x_j^{(n)}\right)}^{\top },j=1,2,\cdots ,Ni=1,2,\cdots ,n{\mathbf{x}}_j\in \mathcal{X}$$

其中，$x_j^{\left(i\right)}$为第$j$个记录的第$i$个属性。（这里为啥要用$\top$转置是因为机器学习中默认向量为列向量，由于列向量太占空间，所以这里用行向量加$\top$转置表示列向量）

标记：描述事物某个特性或结果的事项。
标记值：标记上的取值。
标记空间（输出空间）：标记的所有取值构成的集合，标记空间$\mathcal{Y}$。

样例：拥有了对应标记的记录，由（记录，标记）对表示。第$j$个样例
$$\left({\mathbf{x}}_j,y_j\right),j=1,2,\dots ,N,{\mathbf{x}}_j\in \mathcal{X},y_j\in \mathcal{Y}。$$

数据集：
记录的集合（无监督学习数据集），$D=\{{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_N\}$；
样例的集合（有监督学习数据集），$D=\{\left({\mathbf{x}}_1,y_1\right),\left({\mathbf{x}}_2,y_2\right),\dots ,\left({\mathbf{x}}_N,y_N\right)\}$。

有监督学习：

1. 回归学习：有监督学习中，标记为连续值，$\mathcal{Y}=\mathbb{R}$。
2. 分类学习：有监督学习中，标记为离散值。其中，
   若$|\mathcal{Y}|=2,\mathcal{Y}=\{0,1\}$或$\mathcal{Y}=\{+1,-1\}$，则为二分类；
   若$|\mathcal{Y}|>2,\mathcal{Y}=\{c_1,c_2,\dots ,c_m\}$，则为多分类。

训练数据集：用以训练模型的数据集的子集，$D_{training}\subseteq D$。
验证数据集：用以选择模型的数据集的子集，$D_{verification}\subseteq D$。
测试数据集：应用测试模型的数据集的子集，$D_{testing}\subseteq D$。

1.2 假设空间与参数空间

有监督学习的目的在于学习一个从输入空间$\mathcal{X}$到输出空间$\mathcal{Y}$的映射$f$，或是条件概率$P\left(Y|X\right)$。

决策函数（非概率模型）：从输入空间$\mathcal{X}$到输出空间$\mathcal{Y}$的映射$f:\mathcal{X}\to \mathcal{Y}$。
假设空间$\mathcal{F}$定义为决策函数的集合
$$\mathcal{F}=\left\{f|Y=f\left(\mathbf{X}\right)\right\}$$
其中，$\mathbf{X}$是定义在输入空间$\mathcal{X}$上的变量，$\mathbf{X}\in \mathcal{X}$；$Y$是定义在输出空间$\mathcal{Y}$上的变量，$Y\in \mathcal{Y}$。

假设空间$\mathcal{F}$通常是由一个参数向量决定的函数族
$$\mathcal{F}=\left\{f|Y=f_{\mathbf{w}}\left(\mathbf{X}\right),\mathbf{w}\in {\mathbb{R}}^n\right\}$$
其中，参数向量$\mathbf{w}={\left(w^{\left(1\right)},\cdots ,w^{\left(n\right)}\right)}^{\top }$取值于$n$维向量空间${\mathbb{R}}^n$，称为参数空间。

概率模型：假设空间$\mathcal{F}$定义为条件概率的集合
$$\mathcal{F}=\left\{P|P\left(Y|\mathbf{X}\right)\right\}$$
其中，$\mathbf{X}$是定义在输入空间$\mathcal{X}$上的随机变量，$Y$是定义在输出空间$\mathcal{Y}$上的随机变量。

假设空间$\mathcal{F}$通常是由一个参数向量决定的概率分布族
$$\mathcal{F}=\left\{P|P_{\mathbf{w}}\left(Y|\mathbf{X}\right),\mathbf{w}\in {\mathbb{R}}^n\right\}$$
其中，参数向量$\mathbf{w}$取值于$n$维向量空间${\mathbb{R}}^n$，称为参数空间。

1.3 模型策略

1.3.1 损失函数

损失函数：度量模型预测错误的程度，是模型的预测输出$f\left(\mathbf{X}\right)$和实际输出$Y$的非负实值函数，记作$L\left(Y,f\left(\mathbf{X}\right)\right)$。

$0-1$ 损失函数表示如下
$$\begin{array}{rl}L\left(Y,f\left(\mathbf{X}\right)\right)& =\{\begin{array}{rl}& 1,Y\ne f\left(\mathbf{X}\right)\\ & 0,Y=f\left(\mathbf{X}\right)\end{array}\\ & =I\left(Y\ne f\left(\mathbf{X}\right)\right)\end{array}$$
其中，$I\left(\cdot \right)$是指示函数，当括号中条件成立返回$1$，否则返回$0$。

1.3.2 平方损失函数

$$\begin{array}{r}L\left(Y,f\left(\mathbf{X}\right)\right)={\left(Y-f\left(\mathbf{X}\right)\right)}^2\end{array}$$

1.3.3 绝对值损失函数

$$\begin{array}{r}L\left(Y,f\left(\mathbf{X}\right)\right)=\left|Y-f\left(\mathbf{X}\right)\right|\end{array}$$

1.3.4 对数似然损失函数

$$\begin{array}{r}L\left(Y,P\left(Y|\mathbf{X}\right)\right)=-\log P\left(Y|\mathbf{X}\right)\end{array}$$

1.3.5 经验损失

经验风险（经验损失）是模型$f$关于训练数据集$D$
$$\begin{array}{rl}& \\ & D=\left\{\left({\mathbf{x}}_1,y_1\right),\left({\mathbf{x}}_2,y_2\right),\cdots ,\left({\mathbf{x}}_N,y_N\right)\right\}\end{array}$$
的平均损失
$$\begin{array}{r}{R}_{emp}\left(f\right)=\frac{1}{N}\sum _{i=1}^{N}L\left(y_i,f\left({\mathbf{x}}_i\right)\right)\end{array}$$

学习目标：经验风险最小化
$$f^{\ast }=\underset{f\in \mathcal{F}}{\mathrm{argmin}}{R}_{emp}\left(f\right)$$
其中，$\mathcal{F}$是假设空间。

1.3.6 过拟合

学习时选择的模型复杂，所包含的参数过多，以至于出现对已知数据预测得很好，但对未知数据预测得很差的现象。

1.3.7 欠拟合

学习时选择的模型简单，所包含的参数过少，以至于出现不能对数据预测很好的现象。

1.3.8 泛化能力

学习得到的模型对未知数据的预测能力。

1.3.8 结构风险

在经验风险上增加表示模型复杂度的正则化项。
$$\begin{array}{r}{R}_{str}=\frac{1}{N}\sum _{i=1}^{N}L\left(y_i,f\left({\mathbf{x}}_i\right)\right)+\lambda J\left(f\right)\end{array}$$
其中，$J\left(f\right)$是模型复杂度，是正则化项，是定义在假设空间$\mathcal{F}$上的泛函；$\lambda \ge 0$是系数，用以权衡风险和模型复杂度。

学习目标：结构风险最小化
$$f^{\ast }={\mathrm{argmin}}_{f\in \mathcal{F}}{R}_{str}\left(f\right)$$
其中，$\mathcal{F}$是假设空间。

正则化项可以是参数向量的$L_2$范数
$$J_2=\frac{1}{2}\Vert \mathbf{w}{\Vert }_2^2=\frac{1}{2}{\left(\sqrt{{\left(w^{\left(1\right)}\right)}^2+\cdots +{\left(w^{\left(n\right)}\right)}^2}\right)}^2=\frac{1}{2}\left({\left(w^{\left(1\right)}\right)}^2+\cdots +{\left(w^{\left(n\right)}\right)}^2\right)$$
其中，$\Vert \mathbf{w}{\Vert }_2$表示参数向量$\mathbf{w}$的$L_2$范数。
正则化项可以是参数向量的$L_1$范数
$$J_1=\Vert \mathbf{w}{\Vert }_1=|w^{\left(1\right)}|+\cdots +|w^{\left(n\right)}|$$
其中，$\Vert \mathbf{w}{\Vert }_1$表示参数向量$\mathbf{w}$的$L_1$范数。

1.4 优化算法

机器学习的训练过程就是使用训练数据集$D$，按照模型策略在假设空间$\mathcal{F}$中寻找最优模型$f^{\ast }$的最优化求解过程
$$f^{\ast }={\mathrm{argmin}}_{f\in \mathcal{F}}{R}_{str}\left(f\right)$$或者在参数空间中寻找最优参数${\mathbf{w}}^{\ast }$的最优化求解过程
$${\mathbf{w}}^{\ast }={\mathrm{argmin}}_{f_{\mathbf{w}}\in \mathcal{F}}{R}_{str}\left(f_{\mathbf{w}}\right)。$$

梯度下降法：通过迭代的方法来计算训练集$D$上的风险函数最小值
$$\begin{array}{rl}{\mathbf{w}}_{t+1}& ={\mathbf{w}}_t-\alpha \frac{\partial R_D\left(\mathbf{w}\right)}{\partial \mathbf{w}}\\ & ={\mathbf{w}}_t-\alpha \frac{1}{N}\sum _{i=1}^N\frac{\partial L\left(y_i,f_{\mathbf{w}}\left({\mathbf{x}}_i\right)\right)}{\partial \mathbf{w}}\end{array}$$
其中，${\mathbf{w}}_t$为第$t$次迭代的参数值，$\alpha$为学习率。

1.5 性能度量与评估方法

1.5.1 训练误差

模型$Y=f\left(X\right)$关于训练数据集的平均损失
$$\begin{array}{r}{R}_{emp}\left(f\right)=\frac{1}{N}\sum _{i=1}^{N}L\left(y_i,f\left({\mathbf{x}}_i\right)\right)\end{array}$$
其中，$N$是训练样本容量。

1.5.2 测试误差

模型$Y=f\left(X\right)$关于测试数据集的平均损失
$$\begin{array}{r}{e}_{test}=\frac{1}{N^{\prime }}\sum _{i=1}^{N^{\prime }}L\left(y_i,f\left({\mathbf{x}}_i\right)\right)\end{array}$$
其中，$N^{\prime }$是测试样本容量。

当损失函数是$0-1$损失，测试误差就是测试集上的误差率
$$\begin{array}{r}{e}_{test}=\frac{1}{N^{\prime }}\sum _{i=1}^{N’}I\left(y_i\ne f\left({\mathbf{x}}_i\right)\right)\end{array}$$
其中，$I$是指示函数，即$y\ne f\left(\mathbf{x}\right)$时为1，否则为0。

测试集上的准确率
$$\begin{array}{r}{r}_{test}=\frac{1}{N^{\prime }}\sum _{i=1}^{N’}I\left(y_i=f\left({\mathbf{x}}_i\right)\right)\end{array}$$
则，$r_{test}+e_{test}=1$。

分类中，模型的预测结果可分为：

1. 真正例（True Positive，TP）：将正类预测为正类；
2. 假负类（False Negative，FN）：将正类预测为负类；
3. 假正类（False Positive，FP）：将负类预测为正类；
4. 真负类（True Negative，TN）：将负类预测为负类。

1.5.3 精确率（查准率）

$$\begin{array}{r}P=\frac{TP}{TP+FP}\end{array}$$

1.5.4 召回率（查全率）

$$\begin{array}{r}R=\frac{TP}{TP+FN}\end{array}$$

$F_1$值是精确率和召回率的调和均值
$$\begin{array}{rl}& \\ & \frac{2}{F_1}=\frac{1}{P}+\frac{1}{R}\\ & F_1=\frac{2TP}{2TP+FP+FN}\end{array}$$

真正率
$$TPR=\frac{TP}{TP+FN}$$
假正率
$$FPR=\frac{FP}{TN+FP}$$

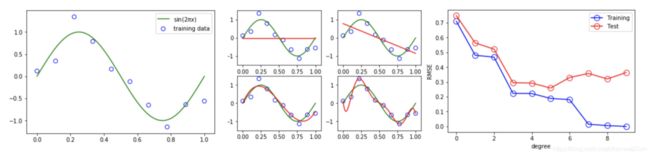
1.6 欠拟合与过拟合实例

import numpy as np
import scipy as sp
from scipy.optimize import leastsq
import matplotlib.pyplot as plt

%matplotlib inline

def real_func(x):
    return np.sin(2 * np.pi * x)

def fit_func(p, x):
    f = np.poly1d(p)
    return f(x)

def residuals_func(p, x, y):
    ret = fit_func(p, x) - y
    return ret

x = np.linspace(0, 1, 10)
x_points = np.linspace(0, 1, 1000)

y_ = real_func(x)
y = [np.random.normal(0, 0.1) + y1 for y1 in y_]

def fitting(M=0):
    p_init = np.random.rand(M + 1)
    p_lsq = leastsq(residuals_func, p_init, args=(x, y))
    print('Fitting Parameters:', p_lsq[0])
    
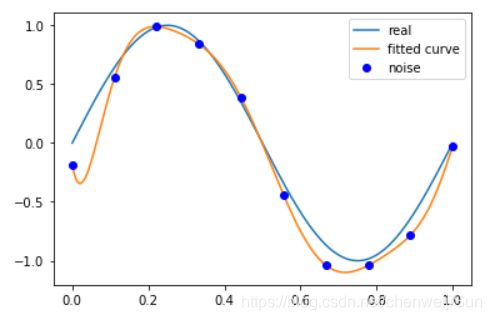
    plt.plot(x_points, real_func(x_points), label='real')
    plt.plot(x_points, fit_func(p_lsq[0], x_points), label='fitted curve')
    plt.plot(x, y, 'bo', label='noise')
    plt.legend()
    return p_lsq

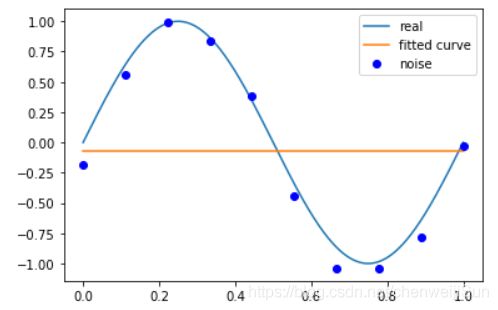
p_lsq_0 = fitting(M=0)

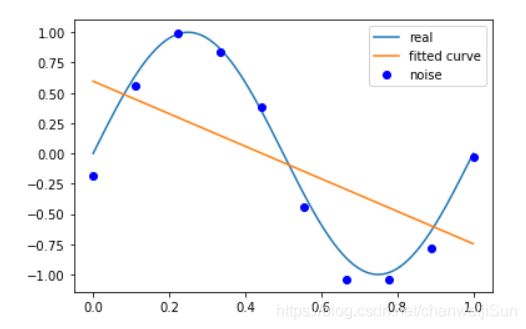
p_lsq_1 = fitting(M=1)

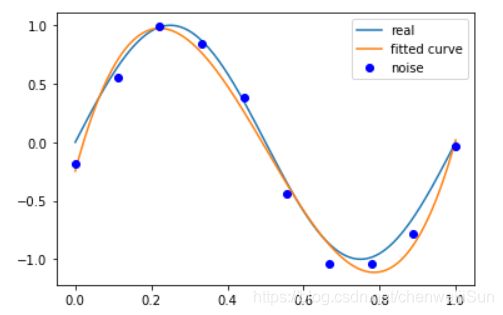
p_lsq_3 = fitting(M=3)

p_lsq_9 = fitting(M=9)

regularization = 0.0001

def residuals_func_regularization(p, x, y):
    ret = fit_func(p, x) - y
    ret = np.append(ret, np.sqrt(0.5 * regularization * np.square(p)))
    return ret

p_init = np.random.rand(9+1)
p_lsq_regularization = leastsq(residuals_func_regularization, p_init, args=(x, y))

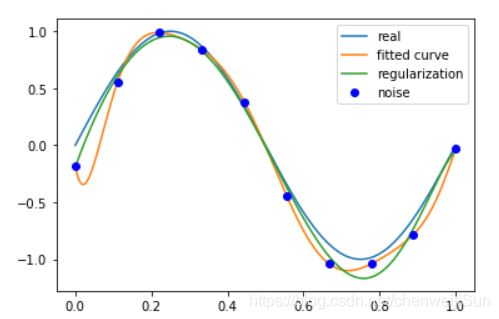
plt.plot(x_points, real_func(x_points), label='real')
plt.plot(x_points, fit_func(p_lsq_9[0], x_points), label='fitted curve')
plt.plot(x_points, fit_func(p_lsq_regularization[0], x_points), label='regularization')
plt.plot(x, y, 'bo', label='noise')
plt.legend()

print(p_lsq_regularization[0])

[ -5.13841552  -2.86712381   1.52815237   6.55153915   9.28063603
5.58868868  -6.8006399  -17.16663939   9.17580857  -0.19034247]