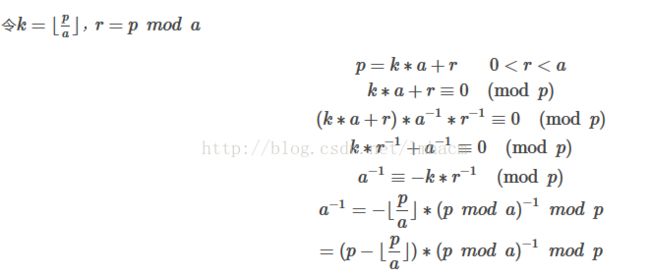求组合数取模（杨辉三角打表 & 求逆元（扩展欧几里得、费马小定理、欧拉定理、线性求法） & Lucas）
在acm竞赛中，组合数取模的题目还是经常会见到的，所以这是有必要掌握的一个算法。我本人就因为这个东西而被坑了很多次了= =之前的博客也都扯过了，就不多说了，下面进入正题。
（1）杨辉三角求组合数
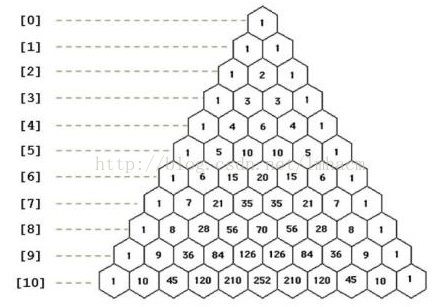
杨辉三角这个东西应该都不陌生，三角的两边始终为一，之后向下累加，组成杨辉三角。
而同样的，这个三角也可以看作一个组合数的表格，比如第三行中，依次可看作为C(3,0)，C(3,1)，C(3,2)，C(3,3)。而通过这个，我们也可以发现一个组合数的规律，即是C(n,m)=C(n-1,m-1)+C(n-1,m)。所以，对于一些数据比较小的题目，我们可以通过用杨辉三角打表求组合数的方法得到需要的数。
int Combination(int n)
{
int i,j;
a[0][0]=1;
for(i=0;i<=n;i++)
{
a[i][0]=a[i][i]=1;
for(j=1;j博客题目链接：http://blog.csdn.net/lmhacm/article/details/52704938
（2）逆元求组合数
而对于一些题目，给出的数据范围很大，就不能用打表的方式来做，需要直接求出组合数才行，我们根据组合数的定义，可以知道组合数的直接求法。
但是这种求法也存在着一定的问题，假如数字太大，可能会爆出long long的内存范围，但是取模处理对于除法并不适用，我们无法将
直接看作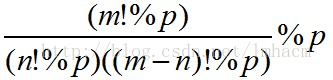
，所以，我们这里需要用求逆元的方式，将这个除法式子改为乘法式子，才可以进行分配开的取模运算。
这里逆元指乘法逆元，假设b存在乘法逆元，即与m互质（充要条件）。设c是b的逆元，即b∗c≡1(mod p)，那么有a/b=(a/b)∗1=(a/b)∗b∗c=a∗c(mod p)，即，除以一个数取模等于乘以这个数的逆元取模。这样就可以将除法计算变为乘法计算，进而进行取模就可以避开出现精度的问题。
如何求逆元也有很多方法：
1、当a和p互质时，逆元求解一般利用扩展欧几里得算法。
2、当p为质数的时候直接使用费马小定理，p为非质数使用欧拉函数。
3、当p为质数的时候，也可使用线性求[1,p-1]所有数逆元的方法。
1、扩展欧几里得
欧几里得算法都很熟悉，就是gcd(a,b)，扩展欧几里得则是一定能找到x和y，使得a*x+b*y=gcd(a,b)，当a与b互质的时候，我们可以得到gcd(a,b)=1，a*x+b*y=1，等式两边同时mod b，即可得到a*x≡1(mod b)，因此x是a%b的逆元。
而用扩展欧几里得求出乘法逆元则是求出最小的x非负整数解，对于x有通解x0+(b/gcd)*t，因此对于最后的结果%b的绝对值便可得到（以防b为负），如果结果为负，则加上abs(b)便可得到最小的结果。
long long exgcd(long long a,long long b,long long &x,long long &y)
{
if(!b)
{
x=1;
y=0;
return a;
}
long long ans=exgcd(b,a%b,x,y);
long long temp=x;
x=y;
y=temp-a/b*y;
return ans;
}
long long cal(long long a,long long b)
{
long long x,y;
long long g=exgcd(a,b,x,y);
if(g!=1)
return -1;
long long ans=x%abs(b);
if(ans<=0)
ans+=abs(b);
return ans;
}2、费马小定理
费马小定理是数论中的一个重要定理，在1636年提出，其内容为： 假如p是质数，且gcd(a,p)=1，那么a(p-1)≡1（mod p），即：假如a是整数，p是质数，且a,p互质(即两者只有一个公约数1)，那么a的(p-1)次方除以p的余数恒等于1。
根据这个公式，进行一下变形可以得到a(p-2)≡a-1（mod p），所以我们可以说a(p-2)为a的乘法逆元。
在求组合数取模的时候，可以对阶乘先进行预处理，之后再通过费马小定理来进行计算便可得到要求的逆元。
int getfac()
{
int i;
fac[0]=1;
for(i=1;i>=1;
a=(a*a)%mod;
}
return ans;
}
long long inv(long long a)
{
return Pow(a,mod-2);
}
long long C(long long n,long long m)
{
if(n 博客题目链接：http://blog.csdn.net/lmhacm/article/details/75923673
3、欧拉定理
在数论，对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目（φ(1)=1）。例如φ(8)=4，因为1,3,5,7均和8互质。
而欧拉定理表明，若a,p为正整数，且a,p互质，则aφ(p)≡1（mod p）。
和前面的费马小定理一样，对这个式子进行变形，可以得到aφ(p)-1≡a-1（mod p），即aφ(p)-1为a的逆元。
当出现p不为质数不能用费马小定理时可以使用，但一般比较少见。
long long euler(int p)
{
long long ans=p,a=p;
long long i;
for(i=2;i*i<=a;i++)
{
if(a%i==0)
{
ans=ans/i*(i-1);
while(a%i==0)
a/=i;
}
}
if(a>1)
ans=ans/a*(a-1);
return ans;
}
long long eu=euler(mod)-1;
long long inv(long long a)
{
return Pow(a,eu);
}
long long C(long long n,long long m)
{
if(n4、线性求逆元
除了上面几种方法还有线性求逆元的方法，通过公式变形得到递推式子然后一次性打出[1,p-1]所有数的逆元，方法转自博客：http://blog.csdn.net/outer_form/article/details/51509360
inv[1]=1;
for(int i=2;i<=n;i++)
inv[i]=(p-p/i)*inv[p%i]%p;
/*递归
int Get_inv(int n){
if(n==1)
return 1;
return (p-p/n)*(Get_inv(p%n))%p;
}*/（3）Lucas定理求组合数
求逆元的方式只适用于较小的数，若数据过大的情况就要用Lucas定理来进行求解。
具体的定理公式如下：
所以在求组合数的时候可以通过Lucas定理来递归求值，具体的证明过程和转化表示我也没看懂= =先记住公式吧......
long long Pow(long long a,long long b)
{
long long ans=1;
while(b)
{
if(b&1)
{
b--;
ans=(ans*a)%p;
}
b>>=1;
a=(a*a)%p;
}
return ans;
}
long long C(long long n,long long m)
{
if(n博客题目链接：http://blog.csdn.net/lmhacm/article/details/54609352
（4）注意
对于大组合数取模C(n,m)，n,m不大于10^5的话，用逆元的方法解决。
对于n,m大于10^5的话，那么要求p<10^5，这样就是Lucas定理了，将n,m转化到10^5以内解。