【数据结构&图论】BZOJ1095Hide 捉迷藏
题目大意
给出一颗树,每个点都是黑/白色,初始状态每个点都是白色的,
有两种操作:
1,翻转某个点的颜色
2,询问整个图中最远的两个白色点的距离(若没有白色点输出-1,只有一个输出0)
分析
本题有 动态点分治/线段树储存括号序列 两种做法。
这里只介绍动态点分治的方法。
这个思路其实非常的淳朴,我们考虑对于单次询问,我们需要的操作:
按重心拆分树,对于每个重心,找到能经过该点的最大路径,最后将每个重心找到的值取最大。
现在考虑将这个过程变成动态的,很容易想到,因为保证最多在logn次以内将一棵树分完,所以如果将重心组成一颗树,如下图:
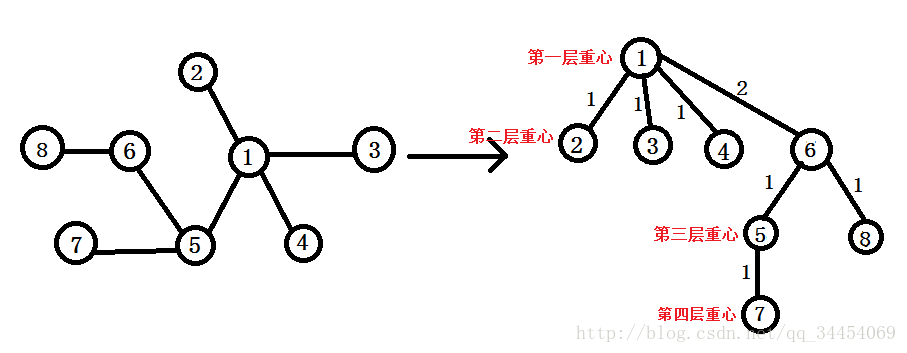
所以,在这颗树中,每个点最多有logn的祖先,也就是说,当我们修改了某个点,它能造成影响的也就只有logn个,所以我们只要依次修改这些点就可以了,
不可避免的就要用到一些神奇的数据结构,(这里我选用了multiset)。
由于LCC表示以上这些看了并不知道怎么实现,所以这道题再介绍一下具体实现。
我们用动态数组存储每个点在更改后的树中的某个祖先,以及到该祖先的距离。
首先,我们对每个重心的每个子树,依次遍历一遍,用当前重心更新每个点的祖先信息,这个过程中,我们就可以按照深度来得到距离信息,没必要之后再写LCA。
整体时间复杂度 O(nlogn)
现在整个树的信息已经处理完了,接下来要动态维护。
这里我们用三个multiset来维护。
第一个:t,表示所有点作为重心时能到找的最大值。
第二个:t2,表示所有点作为重心时某个子树上最远的白色点,因为总子树的个数即为边数,所以这一层有n个multiset,我们需要预先开空间,动态存储的方式实现。
第三个:t3,表示所有点作为重心时,每个子树白色点深度(即t2存储的信息)的最大值,这一层也为n个。
简单地说,我们用t2维护t3,t3维护t,t中最大值就是答案。
这三个multiset之间的维护详见代码。
#include >::iterator
#define MAXN 100010
using namespace std;
multiset<int,greater<int> > t,t2[MAXN],t3[MAXN];
vector<int> rootx[MAXN],len[MAXN],id[MAXN],a[MAXN];
int n,cnt,tot;
int foc[MAXN],sumx[MAXN],sumy[MAXN];
bool vis[MAXN],del[MAXN],delx[MAXN];
int dp(int x,int fa){
vis[x]=1;
for(int i=0;iif(a[x][i]!=fa&&del[a[x][i]]==0)
sumx[x]+=dp(a[x][i],x)+1;
return sumx[x];
}
int dp0(int x,int fa,int root){
sumy[x]=sumx[root]-sumx[x];
for(int i=0;iif(a[x][i]!=fa&&del[a[x][i]]==0)
sumy[x]=max(sumx[a[x][i]]+1,sumy[x]);
int x1=x;
for(int i=0;iif(a[x][i]==fa||del[a[x][i]]==1)
continue;
int x2=dp0(a[x][i],x,root);
if(sumy[x2]return x1;
}
void find_foc(){
cnt=0;
memset(sumx,0,sizeof sumx);
memset(sumy,0,sizeof sumy);
memset(vis,0,sizeof vis);
for(int i=1;i<=n;i++){
if(del[i]==1){
foc[++cnt]=i;
continue;
}
if(vis[i]==0){
dp(i,0);
foc[++cnt]=dp0(i,0,i);
}
}
}
void dfs(int x,int fa,int root,int idx,int sum){
t2[idx].insert(sum);
rootx[x].push_back(root);
len[x].push_back(sum);
id[x].push_back(idx);
for(int i=0;iif(a[x][i]==fa||del[a[x][i]]==1)
continue;
dfs(a[x][i],x,root,idx,sum+1);
}
}
void update(int x){
sit it=t3[x].begin();
if(it==t3[x].end()){
if(delx[x]==1)
return ;
t.insert(0);
}
else{
int maxx=*it;
it++;
if(it==t3[x].end()){
if(delx[x]==1)
return ;
t.insert(maxx);
}
else{
t.insert(maxx+(*it));
}
}
}
void pushdown(int x){
sit it=t3[x].begin();
sit dele;
if(it==t3[x].end()){
if(delx[x]==1)
return ;
dele=t.find(0);
t.erase(dele);
}
else{
int maxx=*it;
it++;
if(it==t3[x].end()){
if(delx[x]==1)
return ;
dele=t.find(maxx);
t.erase(dele);
}
else{
dele=t.find(maxx+(*it));
t.erase(dele);
}
}
}
void push_in(int x){
pushdown(x);
delx[x]^=1;
update(x);
for(int i=0;iint y=rootx[x][i];
int idx=id[x][i];
pushdown(y);
if(t2[idx].empty()==0){
sit dele=t3[y].find(*t2[idx].begin());
t3[y].erase(dele);
}
t2[idx].insert(len[x][i]);
t3[y].insert(*t2[idx].begin());
update(rootx[x][i]);
}
}
void push_out(int x){
pushdown(x);
delx[x]^=1;
update(x);
for(int i=0;iint y=rootx[x][i];
int idx=id[x][i];
pushdown(y);
sit dele=t3[y].find(*t2[idx].begin());
t3[y].erase(dele);
dele=t2[idx].find(len[x][i]);
t2[idx].erase(dele);
if(t2[idx].empty()==0)
t3[y].insert(*t2[idx].begin());
update(rootx[x][i]);
}
}
int u,v,x,m;
char s[10];
int main(){
//freopen("data.in","r",stdin);
//freopen("w.txt","w",stdout);
//freopen("1.txt","w",stdout);
SF("%d",&n);
for(int i=1;i"%d%d",&u,&v);
a[u].push_back(v);
a[v].push_back(u);
}
find_foc();
while(1){
for(int i=1;i<=cnt;i++){
x=foc[i];
if(del[x]==1)
continue;
del[x]=1;
for(int j=0;jif(del[a[x][j]]==1)
continue;
dfs(a[x][j],x,x,++tot,1);
t3[x].insert(*t2[tot].begin());
}
update(x);
}
if(cnt==n)
break;
find_foc();
}
t.insert(-1);
SF("%d",&m);
for(int i=1;i<=m;i++){
SF("%s",&s);
if(s[0]=='G'){
PF("%d\n",*t.begin());
}
else{
SF("%d",&x);
if(delx[x]==1)
push_in(x);
else
push_out(x);
}
}
}