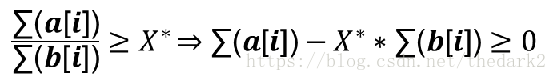图论知识点总结

图的存储

• 链式前向星

const int maxn = 1005;
int head[maxn], cnt;
struct node
{
	int to;		//这条边的终点 
	int next;	//上一条边的存储下标
	int w;		//权值 
}edge[50005];

//加边 
void add(int u, int v, int w)	//起点u，终点v，权值w 
{
	//cnt从0开始计数，即给边编号 
	edge[cnt].to = v;		//存储该边的终点 
	edge[cnt].next = head[u];	//存储以u为起点的上一条边的编号 
	edge[cnt].w = w;		//存储该边的权值 
	head[u] = cnt++;	//head[u]表示以u为起点的至此出现的最后一条边的编号 
}

//遍历（实际是倒序）
for(int i = head[u]; i; i = edge[i].next)
{
	...... 
} 

• 邻接矩阵

• 邻接表

---

种类并查集

• 给定多个集合之间的关系，以及多个个体之间的信息；根据这些信息，我们来判断信息的正确与矛盾，或者将个体进行分类。
• 具体方法是将并查集的容量扩大n倍，用于容纳这多个集合。由于每个元素可能存在于每个集合中，我们关心的只是相对关系，所以具体在哪一个集合中是无关紧要的。(思想类似离散化)

const int maxn = 2010;
struct NODE
{
	int fa;	//father--根节点 
	int rel;//relation--关系（即属于哪个集合） 
} node[maxn];

//初始化 
void Init(int n)	
{
	for(int i=1; i<=n; i++)
	{
		node[i].fa = i;
		node[i].rel = 0;
	}	
} 

//查找根节点 
int Find(int x)
{
	if(x==node[x].fa)	return x;
	int fa = node[x].fa;
	node[x].fa = Find(fa);
	node[x].rel = f1(node[x].rel, node[fa].rel);//f1(a, b)表示当前节点与其根节点的集合转换关系 
	return node[x].fa;
}

//判断两个节点的集合关系 
void union_set(int x, int y)
{
    int rootx = Find(x);
	int rooty = Find(y);
	if(rootx!=rooty)	//合并根节点，转换集合关系 
	{
		node[rooty].fa = rootx;
		node[rooty].rel = f2(node[x].rel, node[y].rel);
	}
	else	
	{
		......//题目条件判断 
	}				    
}

---

Trajan算法

int cnt;	//时间戳 
int scc;	//强连通分量编号 
int stack[maxn];	//栈 
int index;	//栈的序号 
int belong[maxn];	// belong[x]	表示x属于哪个强连通分量
int dfn[maxn];	// dfn[u]	表示u的时间戳 
int low[maxn];	// low[u]	表示u的根节点的时间戳 
int size_[maxn]; 	// size_[scc]	表示编号scc的强连通分量中，有多少个点 
void tarjan(int u)	//实际是DFS 
{
	stack[++index] = u;	//入栈 
	dfn[u] = low[u] = ++cnt;
	int v;
	for(int i=head[u], i, i=edge[i].next)
	{
		v = edge[i].to;
		if(!dfn[v])	//如果没有被访问过 
		{
			tarjan(v);
			low[u] = min(low[u], low[v]);
		}
		else if(!belong[v])	//如果访问过，并且还在栈里
		{
			low[u] = min(low[u], dfn[v]);
		} 
	}
	
	if(low[u]==dfn[u])
	{
		int x;
		++scc;
		while(true)
		{
			x = stack[index--];	//出栈 
			belong[x] = scc;	//x属于第scc个强连通分量 
			size_[scc]++;	//第scc个强连通分量中，点的个数 
			if(x==u)	break;
		}
	}
}

• 强连通分量（有向图） 

定义：有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。（简言之，有向图上的环）

• 双连通分量（无向图）

定义：双连通分量又分点双连通分量和边双连通分量两种。若一个无向图中的去掉任意一个节点（一条边）都不会改变此图的连通性，即不存在割点（桥），则称作点（边）双连通图。一个无向图中的每一个极大点（边）双连通子图称作此无向图的点（边）双连通分量。求双连通分量可用Tarjan算法。

• 割点

定义：在一个无向图中，如果有一个顶点集合，删除这个顶点集合以及这个集合中所有顶点相关联的边以后，图的连通分量增多，就称这个点集为割点集合。

如果某个割点集合只含有一个顶点X（也即{X}是一个割点集合），那么X称为一个割点

• 割边（桥）

定义：假设有连通图G，e是其中一条边，如果G-e是不连通的，则边e是图G的一条割边。此情形下，G-e必包含两个连通分支。

• 割点割边算法

• 若low[v]>=dfn[u],则u为割点，u和它的子孙形成一个块。因为这说明u的子孙不能够通过其他边到达u的祖先，这样去掉u之后，图必然分裂为两个子图。
• 若low[v]>dfn[u],则(u,v)为割边。理由类似于上一种情况。

关于tarjan算法比较详细的解读（转） https://blog.csdn.net/qq_34374664/article/details/77488976

---

生成树

最小生成树

关于最小生成树这篇写得很好理解 https://blog.csdn.net/gettogetto/article/details/53216951

我就把代码贴一下吧

• Prim算法

#include
#define INF 10000
using namespace std;
const int maxn = 6;
bool vis[maxn];
int dist[maxn];
int graph[maxn][maxn];	//graph[u][v]表示从u到v的权值，INF代表两点之间不可达 
int prim(int cur)
{
    int index = cur;
    int sum = 0;
    cout<graph[index][j])//执行更新，如果点距离当前点的距离更近
                                                //就更新dist
            {
                dist[j] = graph[index][j];
            }
        }
    }
    cout<

• Kruskal算法

#include
using namespace std;
const int maxn = 7;
typedef struct _node
{
    int val;
    int start;
    int end;
}Node;
Node V[maxn];
int cmp(const void *a, const void *b)
{
    return(*(Node *)a).val - (*(Node *)b).val;
}
int fa[maxn];
int cap[maxn];
 
void make_set()              //初始化集合，让所有的点都各成一个集合，每个集合都只包含自己
{
    for(int i=0; i

（有点并查集的意思）

次小生成树

枚举非树边，删掉以该非树边两端点在树上路径中最大的一条边，并换上这条边然后计算目前答案，最后将所有算出的答案取min（简单带过）

最小度限制生成树

定义：满足定点 的度数  这一条件的生成树称为度限制生成树。把权值和最小的度限制生成树称为最小度限制生成树。

1. 删掉与  相连的边，得到m个连通块，求出最小m度限制生成树
2. 由最小m度限制生成树，得到最小m+1度限制生成树：

         枚举所有和 相邻点v，添加边(, v)，可知一定会出现一个环。

         删掉环上与 不相连的权值最大的边，计算权值的改变，取最优。

         （环上与 不相连的权值最大的边：Tree DP）

    3. 直到 的度数

最优比率生成树

• 01分数规划

     

   

   

   

• 最优比率生成树

   

   

最小树形图

定义：一个有向图的生成树，如果从给定点 出发能到达其余所有点，并且权值和最小的生成树就是最小树形图。

1. 找到除了 以外其他点的权值最小的入边，记为 in[i] ，如果不存在环则 in[i] 的集合就是最小树形图
2. 如果存在环则将环缩成一个点，重新计算最小树形图
3. 直到不存在环

---

二分图

• 二分图匹配

• 匈牙利算法

• 最小点覆盖

• 最小路径覆盖

• 最大独立集

• Ramsey定理

（还不会，以后更啊）

---

网络流

定义：在一个有向图上选择一个源点，一个汇点，每一条边上都有一个流量上限（一般称为容量），即经过这条边的流量不能超过这个上界，同时，除源点和汇点外，所有点的入流和出流都相等，而源点只有流出的流，汇点只有汇入的流。这样的图叫做网络流。

源点：只有流出去的点
汇点：只有流进来的点
流量：一条边上流过的流量
容量：一条边上可供流过的最大流量
残量：一条边上的容量-流量

• 最大流（Dinic算法）

具体可参考 http://www.cnblogs.com/SYCstudio/p/7260613.html

• 最小割（=最大流）

定义：给定一个网络，如果去掉一些边则无法从源点S到达汇点T，则这些边就是一个割集。容量之和最小的割集叫最小割。

• 费用流（最小费用最大流）

定义：如果每条边还有一个单位流量的费用cost(u,v)，要求在流量最大的前提下总费用最小，这样的问题称之为最小费用最大流。

1. 设当流量达到v(F)时的最小费用流为F
2. 找一条费用最小的增广路，得到流量为v(F)+1的最小费用流
3. 直到流量达到最大，即找不到增广路

反向边的费用：cost(v,u) = -cost(u,v)

第二步：可以直接得到流量为v(F) + Rmin的最小费用流

找费用最小的增广路：SPFA