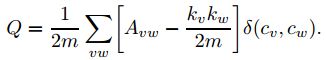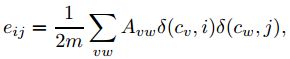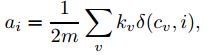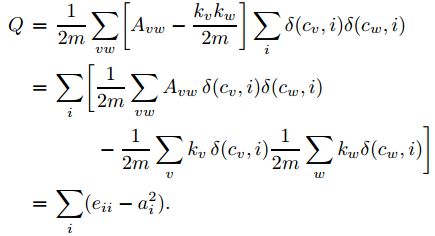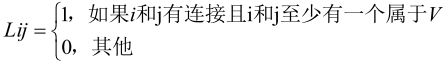在做东西的时候用到了社区发现的算法,因此查找了好多人的文章,发现一个不错的总结,先转载过来
原文出处http://blog.csdn.net/aspirinvagrant/article/details/45577033
在社区发现算法中,几乎不可能先确定社区的数目,于是,必须有一种度量的方法,可以在计算的过程中衡量每一个结果是不是相对最佳的结果。
模块度(Modularity)用来衡量一个社区的划分是不是相对比较好的结果。一个相对好的结果在社区内部的节点相似度较高,而在社区外部节点的相似度较低。
全局模块度
设AVW 为网络的邻接矩阵的一个元素,定义为:
假设cv和cw分别表示点v和点w所在的两个社区,社区内部的边数和网络中总边数的比例:
函数δ(cv,cw)的取值定义为:如果v和w在一个社区,即cv=cw,则为 1,否则为 0。m 为网络中边的总数。
模块度的大小定义为社区内部的总边数和网络中总边数的比例减去一个期望值,该期望值是将网络设定为随机网络时同样的社区分配所形成的社区内部的总边数和网络中总边数的比例的大小,于是模块度Q为:
其中kv表示点v的度。
设eij表示社区i和社区j内部边数目的和与总边数的比例,ai表示社区i内部的点所关联的所有的边的数目与总边数的比例。
为了简化Q的计算,假设网络已经划分成n个社区,这个时候就有一个 n维矩阵,Q 的计算可以变成:
在进行每次划分的时候计算Q值,Q取值最大的时候则是此网路较理想的划分。Q值的范围在0-1之间,Q值越大说明网络划分的社区结构准确度越高,在实际的网络分析中,Q值的最高点一般出现在0.3-0.7之间。
局部模块度
有时候,可能不知道全网络的数据,可以用局部社区的局部模块度的方式来检查社区的合理性。假设有一个已经检测出来的社区,社区的节点的集合为V,这些节点所有的邻接节点而加入到集合当中来,形成新的集合V*。定义V*的邻接矩阵为:
于是,和全局模块度相似的是,可以用节点集V*全部属于节点集V中的元素所占的比例的大小来衡量一个社区的好坏:
其中,δ(i,j)表示的是如果i,j都是V中则值为1,否则为0。m*表示的是邻接矩阵内边的数目。
局部模块度比全局模块度要快的多,因为局部模块度的计算只需要用到局部的网络信息,只需要在刚刚开始的时候扫描一下整个网络。对于中小规模的网络可能局部模块度的效果要低于全局模块度,但是而且对于中等或者大规模的社会网络来说,局部模块度的效果可能还要好一些。
参考资料:
Finding community structure in very large networks
社区发现算法(一)
图分割方法大多是基于迭代二分法的,基本思想是将图分割成两个子图,然后迭代,最后得出要求的子图数。经典的算法有Kernighan-Lin算法和谱二分算法。
K-L(Kernighan-Lin)算法
K-L(Kernighan-Lin)算法是一种将已知网络划分为已知大小的两个社区的二分方法,它是一种贪婪算法。它的主要思想是为网络划分定义了一个函数增益Q,Q表示的是社区内部的边数与社区之间的边数之差,根据这个方法找出使增益函数Q的值成为最大值的划分社区的方法。具体策略是,将社区结构中的结点移动到其他的社区结构中或者交换不同社区结构中的结点。从初始解开始搜索,直到从当前的解出发找不到更优的候选解,然后停止。
K-L算法的缺陷是必须先指定了两个子图的大小,不然不会得到正确的结果,实际应用意义不大。
谱二分算法
当网络中存在两个社区结构时,就能够根据非零特征值所对应的特征向量中的元素值进行结点划分。把所有正元素对应的那些结点划分为同一个社区结构,而所有负元素对应的结点划分为另外一个社区结构。
谱二分算法利用的是Laplace矩阵的特征值和特征向量的性质来做社区划分。Laplace矩阵的第二小特征值λ2的值越小,划分的效果就越好。所以谱二分法使用Laplace矩阵的第二小特征值来划分社区。
谱平分法的缺陷是,一次只能划分2个社区,如果需要划分多个,需要执行多次。如果只需要划分两个社区,谱平分法的效率比较高,但是要划分多个社区的时候,铺平分法的效率就不高了,它的优点也不能得到充分的体现,而且准确度也可能会降低。
社区发现算法(二)
GN算法
本算法的具体内容请参考Finding and evaluating community structure in networks(Newman and Girvan)。
重要概念
边介数(betweenness):网络中任意两个节点通过此边的最短路径的数目。
![]()
GN算法的思想:
在一个网络之中,通过社区内部的边的最短路径相对较少,而通过社区之间的边的最短路径的数目则相对较多。下图中展示了变得强度以及边介数在现实网络中的分布情况。GN算法是一个基于删除边的算法,本质是基于聚类中的分裂思想,在原理上是使用边介数作为相似度的度量方法。在GN算法中,每次都会选择边介数高的边删除,进而网络分裂速度远快于随机删除边时的网络分裂。
![]()
GN算法的步骤如下:
(1)计算每一条边的边介数;
(2)删除边界数最大的边;
(3)重新计算网络中剩下的边的边阶数;
(4)重复(3)和(4)步骤,直到网络中的任一顶点作为一个社区为止。
GN算法示例:
![]()
GN算法计算边界数的时间复杂度为 O(m*n),总时间复杂度在m条边和n个节点的网络下为 O(m2*n)。
GN算法的缺陷:
(1)不知道最后会有多少个社区;
(2)在计算边介数的时候可能会有很对重复计算最短路径的情况,时间复杂度太高;
(3)GN算法不能判断算法终止位置。
为了解决这些问题,Newman引入了模块度Q的概念,它用来一个评价社区结构划分的质量。网络中的社区结构之间的边数并不是绝对数量上的少,而是应该比期望的边数要少。关于模块度的概念请参考社区划分的标准--模块度。
GN算法具体实现借助基于R的图挖掘库igraph。
数据集为Karate数据集:
Zachary空手道俱乐部成员关系网络是复杂网络、社会学分析等领域中最常用的一个小型检测网络之一。从1970到1972年,Zachary观察了美国一所大学空手道俱乐部成员间的社会关系,并构造出了34个成员,78条成员关系的社会关系网。两个成员经常一起出现在俱乐部活动之外的其他场合,就认为两个成员间有边。该俱乐部因为主管(节点34)与教练(节点1)之间的争执而分裂成2个各自为核心的小俱乐部。结构如下图所示。具体请参考An information flow model for conflict and fission in small groups。
![]()
GN算法的R分析代码
> library("igraph")
> karate <- graph.famous("Zachary")
> ebc <- edge.betweenness.community(karate)
> ebc
Graph community structure calculated with the edge betweenness algorithm
Number of communities (best split): 5
Modularity (best split): 0.4012985
Membership vector:
[1] 1 1 2 1 3 3 3 1 4 5 3 1 1 1 4 4 3 1 4 1 4 1 4 4 2 2 4 2 2 4 4 2 4 4
> modularity(ebc)
[1] 0.4012985
> membership(ebc)
[1] 1 1 2 1 3 3 3 1 4 5 3 1 1 1 4 4 3 1 4 1 4 1 4 4 2 2 4 2 2 4 4 2 4 4
> plot(ebc,karate)
![]()
Newman快速算法
本算法的具体内容请参考Fast algorithm for detecting community structure in networks(Newman)。
GN算法通过模块度可以准确的划分网络,但它只适用于中小型规模的网络。Newman提出一种基于贪心的快速社区发现算法,算法的基本思想是:首先将网络中的每个顶点设为一个单独社区,然后选出使得模块度Q的增值最大的社区对进行合并;如果网络中的顶点属于同一个社区,则停止合并过程。整个过程是自底向上的过程,且这个过程最终得到一个树图,即树的叶子节点表示网络中的顶点,树的每一层切分对应着网络的某个具体划分,从树图的所有层次划分中选择模块度值最大的划分作为网络的有效划分。
设网络有n个节点,m条边,每一步合并对应的社区数目为r,组成一个r*r矩阵e,矩阵元素eij表示社区i中的节点与社区j中节点之间连边的数目在网络总变数的百分比。
主要步骤:
(1) 初始化网络,开始网络有n 个社区,初始化的eij和ai为:
![]()
(2)依次按照∆Q的最大或者最小的方向进行合并有边相连的社区对,并计算合并后的模块度增量∆Q:
![]()
(3)合并社区对以后修改对社区对称矩阵e 和社区i和j对应的行列;
(4)重复执行步骤(2)和(3),不断合并社区,直至整个网络合并成一个社区为止。
Newman快速算法的R分析代码
> karate <- graph.famous("Zachary")
> fc <- fastgreedy.community(karate)
> dendPlot(fc)
![]()
参考资料:
Social and Information Network Analysis Jure Leskovec, Stanford University