HDU - 1255 覆盖的面积(线段树-矩形交面积)

题目链接：

HDU - 1255

题目大意：

以左下点和右上点的形式给 n 个矩形，求出被这些矩形覆盖过至少两次的区域的面积。(多组)

数据范围：

1≤T≤1001≤n≤10000≤xi,yi≤100000

解题思路：

学会了矩形并面积之后，这道题就很好理解了。只需要得到 总区间被覆盖了 两次及以上的 区间长度，用同样的方法就可以求得答案。
这道题 n只有1000 ，所有每次更新到叶子节点时间也够了。这个就比区间修改简洁多了：

void update(int rt, int L, int R, int f) {
    if(tree[rt].l == tree[rt].r) {
        lazy[rt] += f;
        if(lazy[rt] > 1) tree[rt].len = x[tree[rt].r + 1] - x[tree[rt].l];
        else tree[rt].len = 0;
        return;
    }
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if(L <= mid) update(rt << 1, L, R, f);
    if(R > mid) update(rt << 1 | 1, L, R, f);
    tree[rt].len = tree[rt << 1].len + tree[rt << 1 | 1].len;
    //len表示被覆盖了两次及以上的区间长度
}

不过，区间更新肯定更快啊！所以还是建议区间修改。
以下所描述的变量或数组含义全同代码。
在线段树中定义两个变量 one和more ，分别表示当前节点所管辖区间被 覆盖一次及以上 和 覆盖两次及以上 的长度。在区间更新中，值得注意的是，父亲节点若的覆盖情况会受儿子节点的影响。最大的影响就是：当父亲节点被覆盖了一次时，若儿子节点也被覆盖了，那么父亲节点的覆盖次数就不再是一次了！
举个例子：对区间 [1,4] 建立线段树，如图：

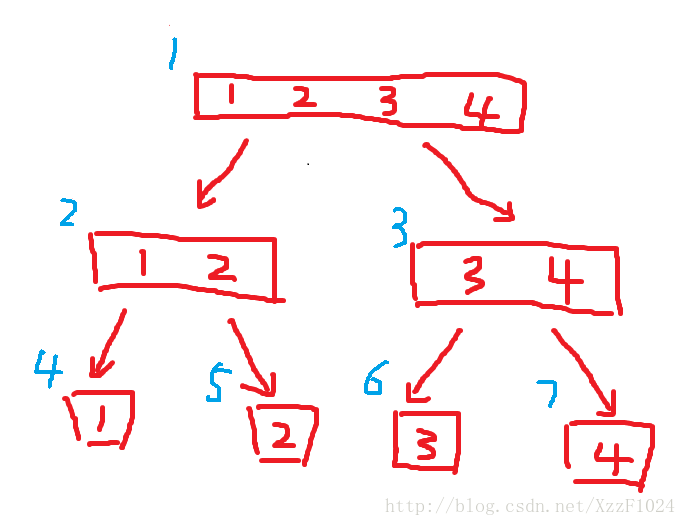
左上角是各节点的标号。
现依次覆盖区间 [1,3]和[2,4] ，那么update之后， lazy[2],lazy[3],lazy[5],lazy[6] 都等于 1 (此处 lazy[]含义同代码，表示这个节点所管辖区间被覆盖了多少次 )。
现在就出现了上面说的那种情况，以 2 号节点为例。 lazy[2]==1 ，其右儿子 lazy[5] 也是等于 1 的，此时就需要根据左右儿子的覆盖情况来更新父亲节点的 more 。得到 tree[2].more=1 ，同理得 tree[3].more=1 ，最后向上更新出 tree[1].more=2 。
详见代码push_up()。

一直想不明白为什么代码71和72行交换就会WA，望好心大佬指点迷津！

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long LL;
const int inf = 1 << 30;
const LL INF = 1LL << 60;
const int MaxN = 1005;

int n, T;
int m, k;
struct Segment 
{
    double xl, xr;
    double h;
    int flag;
    Segment() {}
    Segment(double a, double b, double c, int d) {
        xl = a; xr = b; h = c; flag = d;
    }
    bool friend operator < (Segment a, Segment b) {
        if(a.h == b.h) return a.flag > b.flag;
        else return a.h < b.h;
    }
}seg[2 * MaxN + 5];

double x[2 * MaxN + 5];

struct segtree
{
    int l, r;
    double one;     //当前节点所管辖区间被覆盖 一次及以上的长度
    double more;    //当前节点所管辖区间被覆盖 两次及以上的长度
}tree[8 * MaxN + 5];
int lazy[8 * MaxN + 5]; //lazy[rt]表示节点rt所管辖区间被覆盖了多少次

void Build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    tree[rt].one = 0.0; tree[rt].more = 0.0;
    lazy[rt] = 0;
    if(l == r) return;
    int mid = (l + r) >> 1;
    Build(rt << 1, l, mid);
    Build(rt << 1 | 1, mid + 1, r);
}

int bin_search(double val) { //查找数组x中大于等于val的最小位置
    int l = 1, r = k;
    int mid = 0, res = 0;
    while(l <= r) {
        mid = (l + r) >> 1;
        if(x[mid] >= val) res = mid, r = mid - 1;
        else l = mid + 1;
    }
    return res;
}

//先更新one,这显而易见
void push_up(int rt) {
    if(lazy[rt] > 0) tree[rt].one = x[tree[rt].r + 1] - x[tree[rt].l];  //若覆盖多次,直接更新one
    else if(tree[rt].l == tree[rt].r) tree[rt].one = 0.0;               //若为叶子节点,one为0
    else tree[rt].one = tree[rt << 1].one + tree[rt << 1 | 1].one;      //否则,由左右儿子更新

    if(lazy[rt] >= 2) tree[rt].more = x[tree[rt].r + 1] - x[tree[rt].l];
    else if(tree[rt].l == tree[rt].r) tree[rt].more = 0.0;                  //71和72换了位置就WA,想想
    else if(lazy[rt] == 1) tree[rt].more = tree[rt << 1].one + tree[rt << 1 | 1].one;
    else tree[rt].more = tree[rt << 1].more + tree[rt << 1 | 1].more;
    /*more基本同理,重点是lazy[rt] == 1时,若当前区间已被覆盖一次,且左右儿子也被覆盖过一次
    回溯回来就相当于当前区间被覆盖了两次*/
}

void update(int rt, int L, int R, int f) {
    if(L <= tree[rt].l && tree[rt].r <= R) {
        lazy[rt] += f;
        push_up(rt);
        return;
    }
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if(L <= mid) update(rt << 1, L, R, f);
    if(R > mid) update(rt << 1 | 1, L, R, f);
    push_up(rt);
}

int main()
{
    scanf("%d", &T);
    while(T--) {
        m = 0; 
        scanf("%d", &n);
        for(int i = 1; i <= n; i++) {
            double x1, y1, x2, y2;
            scanf("%lf %lf %lf %lf", &x1, &y1, &x2, &y2);
            x[++m] = x1;
            seg[m] = Segment(x1, x2, y1, 1);
            x[++m] = x2;
            seg[m] = Segment(x1, x2, y2, -1);
        }
        sort(x + 1, x + m + 1);
        sort(seg + 1, seg + m + 1);
        k = 1;
        for(int i = 2; i <= m; i++) //去重,离散
            if(x[i] != x[i - 1])
                x[++k] = x[i];
        Build(1, 1, k - 1);
        double ans = 0.0;
        for(int i = 1; i <= m - 1; i++) {
            int L = bin_search(seg[i].xl);
            int R = bin_search(seg[i].xr) - 1;
            //printf("%d %d\n", L, R);
            update(1, L, R, seg[i].flag);
            ans += tree[1].more * (seg[i + 1].h - seg[i].h);
        }
        printf("%.2lf\n", ans);
        memset(x, 0, sizeof(x));
        memset(seg, 0, sizeof(seg));
        memset(tree, 0, sizeof(tree));
    }
    return 0;
}

降阶版：矩形并面积
进阶版：矩形并周长