分治-Acwing-逆序对的数量
分治-Acwing-逆序对的数量
题目:
给定一个长度为n的整数数列,请你计算数列中的逆序对的数量。
逆序对的定义如下:对于数列的第 i 个和第 j 个元素,如果满足 i < j 且 a[i] > a[j],则其为一个逆序对;否则不是。
输入格式
第一行包含整数n,表示数列的长度。
第二行包含 n 个整数,表示整个数列。
输出格式
输出一个整数,表示逆序对的个数。
数据范围
1≤n≤100000
输入样例:
6
2 3 4 5 6 1
输出样例:
5
题解:
首 先 , 最 暴 力 的 做 法 , 两 重 循 环 i , j 遍 历 数 组 a , 对 每 一 个 a [ i ] , 遍 历 出 剩 下 所 有 的 a [ j ] < a [ i ] , O ( n 2 ) 。 首先,最暴力的做法,两重循环i,j遍历数组a,对每一个a[i],遍历出剩下所有的a[j]
考 虑 分 治 法 优 化 , 对 区 间 [ l , r ] 之 间 的 逆 序 对 的 数 量 , 可 以 分 为 三 个 部 分 : ① 、 i , j 在 区 间 [ l , m i d ] , ② 、 i , j 在 区 间 [ m i d + 1 , r ] 之 间 , ③ 、 i 在 [ l , m i d ] 中 , j 在 [ m i d + 1 , r ] 中 。 考虑分治法优化,对区间[l,r]之间的逆序对的数量,可以分为三个部分:\\①、i,j在区间[l,mid],②、i,j在区间[mid+1,r]之间,③、i在[l,mid]中,j在[mid+1,r]中。 考虑分治法优化,对区间[l,r]之间的逆序对的数量,可以分为三个部分:①、i,j在区间[l,mid],②、i,j在区间[mid+1,r]之间,③、i在[l,mid]中,j在[mid+1,r]中。
对 于 第 ③ 部 分 , 由 于 a [ i ] , a [ j ] 分 居 两 边 , 因 此 将 两 边 区 间 有 序 与 否 不 会 影 响 逆 序 对 数 量 的 统 计 , 所 以 可 以 将 两 边 区 间 排 序 后 再 统 计 , 这 样 可 以 将 第 三 部 分 的 复 杂 度 降 到 O ( l o g 2 n ) 。 对于第③部分,由于a[i],a[j]分居两边,因此将两边区间有序与否不会影响逆序对数量的统计,\\所以可以将两边区间排序后再统计,这样可以将第三部分的复杂度降到O(log_2n)。 对于第③部分,由于a[i],a[j]分居两边,因此将两边区间有序与否不会影响逆序对数量的统计,所以可以将两边区间排序后再统计,这样可以将第三部分的复杂度降到O(log2n)。
这 其 实 是 一 个 归 并 排 序 的 过 程 , 边 排 序 边 计 算 。 整 个 复 杂 度 O ( n l o g 2 n ) 。 这其实是一个归并排序的过程,边排序边计算。整个复杂度O(nlog_2n)。 这其实是一个归并排序的过程,边排序边计算。整个复杂度O(nlog2n)。
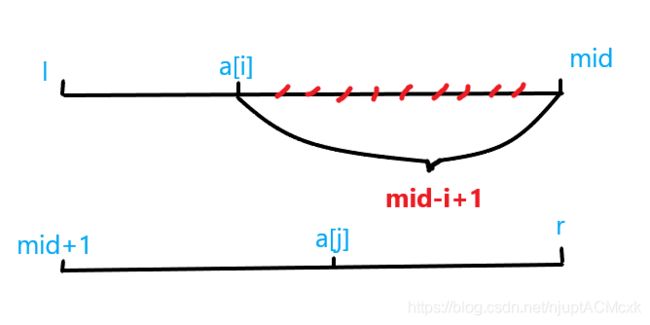
如 上 图 , 若 a [ i ] > a [ j ] , 那 么 从 下 标 i 到 m i d 的 所 有 元 素 都 大 于 a [ j ] , 数 量 为 m i d − i + 1 。 如上图,若a[i]>a[j],那么从下标i到mid的所有元素都大于a[j],数量为mid-i+1。 如上图,若a[i]>a[j],那么从下标i到mid的所有元素都大于a[j],数量为mid−i+1。
归并排序模板:
#include本题代码:
注意:
由 于 数 据 范 围 是 1 0 5 , 当 数 组 是 逆 序 时 , 最 大 答 案 达 到 ( n − 1 ) ( n − 2 ) 2 , 大 约 在 5 × 1 0 9 爆 了 i n t , 故 答 案 用 l l 存 。 由于数据范围是10^5,当数组是逆序时,最大答案达到\frac{(n-1)(n-2)}{2},大约在5×10^9爆了int,故答案用ll存。 由于数据范围是105,当数组是逆序时,最大答案达到2(n−1)(n−2),大约在5×109爆了int,故答案用ll存。
#include
return 0;
}