在这里先不谈计算机中栈,二叉树等抽象结构,而把问题更加一般化,以让更多的人了解卡特兰数。
下面思考这么一个问题:有2n(n>=1)个人排成一队进入剧场。入场费5元,其中有n个人每人只有一张5元的钞票,另外n个人每人只有一张10元的钞票,且售票口处无备用钞票。
问有多少种排队方式使得只要有10元的人买票,售票处就有5元的钞票找零?
该问题的解就是一个著名的数列:卡特兰数-----C(2n,n)/(n+1)。
可以从该类问题中抽象出这样一种数学模型:
对于一个只含有两种操作(设为操作1,操作2)的问题,问题的解是由这两种操作构成的排列,并且操作1的总数等于操作2的总数,任取前k项(k>=1),若满足操作1的个数大于等于操作2的个数才是问题的一种解,则问题解的个数就是卡特兰数。如:上述问题中操作1就可以看作有5元钞票的人,操作2看作有10元钞票的人,则只有当任意前k个人(k>=1)中,拿着5元钞票的人数多于或者等于拿着10元钞票的人数的时候,售票处才有5元的钞票找零.这种排队方式的种数为C(2n,n)/(n+1)
卡特兰数的代数递推式让人眼花缭乱,然而用几何解析法却让人有种豁然开朗的感觉,这里就用折线法来证明它:
证:
设某个人初始时站在原点,不妨设操作1为此人向右上45°角方向走1步(步长设为根号2),操作2为向右下45°角方向走1步,此人总共走了2n步,且操作1的次数等于操作2的次数;
⑴总的折线种数(人的走法)就是从这2n步中任取n步为操作1,即C(2n,n);
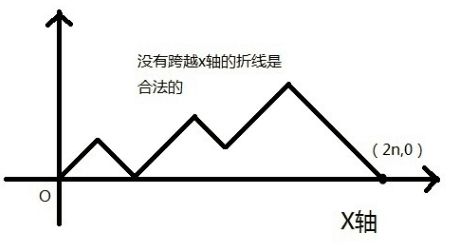
⑵若任取前k(k>=1)次操作满足操作1的个数大于等于操作2的个数,表现在折线图中就是没有跨越x轴,并且最终一定是走到(2n,0)点。此时的折线就是问题的合法解,
如下图所示:
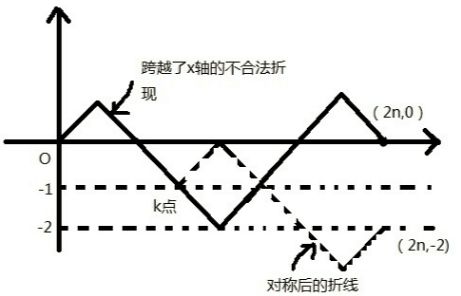
⑶若折线有跨越x轴的部分,则不合法。对于任意一条跨越x轴的折线必与y=-1直线相交,取第一次与其相交的点k,将k点右方的折线关于y = -1直线作对称折线(即操作1与操作2对换),可以发现折线的终点最终都会从点(2n,0)对称到点(2n,-2),由于对称总是能进行的且是可逆的(一一对应),所以不合法的折线种数就转化成了下图所示的从(0,0)到(2n,-2)折线的种数,而该种折线代表的操作2的个数比操作1的个数多2次,即操作1有n-1次,操作2有n+1次,所以种数为从这2n次操作中任选n-1次为操作1,即C(2n,n-1);
则合法解的种数 = 总的 - 不合法的 = C(2n,n) - C(2n,n-1) ;
不合法的 = C(2n,n-1) = (2n)! / ((n+1)! * (n-1)!) = ((2n)! * n) / ((n+1) * n! * n!) = (n / (n+1)) * C(2n,n);
所以合法解的种数(catalan数) = C(2n,n) - C(2n,n-1) = C(2n,n) - (n / (n+1)) * C(2n,n) = C(2n,n)/(n+1)。
证毕.
卡特兰数的几个应用:
1.以某次序入栈序列的出栈可能性
2.n个结点组成不同二叉树的种数问题
2.摞盘子与抽盘子同时进行的问题
卡特兰数还有诸多应用,渗透各领域,在这里就不再赘述了。