数字图像处理第八章 图像压缩

图像压缩是数字图像处理中商业化最成功的一个应用方面，无论在图像传输还是图像存储中都发挥了巨大的作用，图像压缩讨论如何减少描述数字图像的数据量的问题。压缩是通过去除一个或三个基本数据冗余来达到的：1）编码冗余，当所用的码字大于最佳编码（也就是最小长度）时存在编码冗余；2）空间或/和时间冗余，也就是因为一幅图像的像素间，或是图像序列中相邻像素间的相关性而造成的冗余；3）无关信息，也就是源于人类视觉系统而忽略的数据冗余（视觉上不重要的信息）。在本章中，我们研究每种冗余，讨论去除冗余的几种技术，并考察两种重要的压缩标准——JPEG和JEPG 2000。这两种标准通过结合三种数据冗余去除技术统一了在本章最初介绍的概念。

1 背景

这里我们用后面将要学到的JPEG压缩的过程来举例：

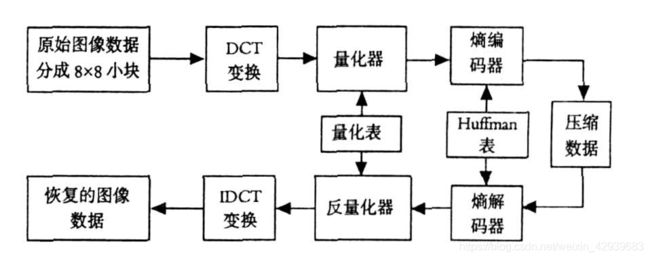
正如上图中可以看到的那样，图像压缩系统是由两个截然不同的数据块组成的：第一行的编码器和第二行的解码器。图像f(x,y)被送入编码器，编码器从输入数据建立一组符号，并用它们描述图像。如果令n₁和n₂分别表示原始及编码后的图像携带的信息单元的数量（通常为比特），达到的压缩可以通过压缩比，用数字进行量化：$$C_R=\frac{n_1}{n_2}$$可能是10（10：1）压缩比，这指出在压缩过的数据集中，对于每一个单元，原始图像有10个携带信息的单元（如比特）。在MATLAB中，用于表示两幅图像文件或变量的比特数的比率可通过下面的M-函数计算出来：

function cr = imratio(f1, f2)
narginchk(2, 2);        
cr = bytes(f1) / bytes(f2);          

function b = bytes(f)  
if ischar(f)
   info = dir(f);        b = info.bytes;
elseif isstruct(f)
   b = 0;
   fields = fieldnames(f);
   for k = 1:length(fields)
      elements = f.(fields{k});
      for m = 1:length(elements)
          b = b + bytes(elements(m));
      end
   end
else
   info = whos('f');     b = info.bytes;
end

例如，JPEG编码图像的压缩可以通过以下命令进行计算：

>> r = imratio(imread('raccoon.jpg'),'raccoon.jpg')

r =

    8.6463

结果表示对于我们的特定JPEG图像压缩比可以达到8比1，观察并运用压缩的（也就是编码后的）图像，必须把图像发送到解码器，这里产生重建的输出图像f^~(x,y)。一般而言，f^~(x,y)可能是，也可能不是f(x,y)的精确表示。如果是，系统就是无误差的、信息保持的或无损的；如果不是，在重建图像中会有一部分失真。对于后一种情况，被称为有损压缩，可以对x和y的任意取值在f(x,y)和f^~(x,y)之间定义误差e(x,y)：$$e(x,y)=\hat{f}(x,y)-f(x,y)$$所以，两幅图像间的总误差为：$$\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}[\hat{f}(x,y)-f(x,y)]$$同时，f(x,y)和f^~(x,y)之间的均方根误差e_rms是M×N数组的均方误差的平均值的平方根：$$e_{rms}=[\frac{1}{MN}\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}[\hat{f}(x,y)-f(x,y){]}^2{]}^{1/2}$$

2 编码冗余

令具有概率p_r(r_k)的随机变量为r_k，其中k=1,2,…,L，描述灰度图像的灰度级。正如在第二章中那样，r₁对应灰度级0且：$$p_r(r_k)=\frac{n_k}{n}k=1,2,...,L$$这里的n_k是图像中出现第k级灰度的次数，n是图像的总像素数。如果用于表示每个r_k值的比特数是l(r_k)，那么表示每个像素的平均比特数是：$$L_{age}=\sum _{k=1}^{L}l(r_k)p_r(r_k)$$也就是说，分配给各种灰度级的码字的平均长度是由用于表示每个灰度级的比特数和可能出现的灰度级的概率乘积之和建立的。这样一来，M×N大小的图像要求的总比特殊便是MNL_agv。当用m比特的自然二进制码表示一幅图像的灰度级时，前面等式右边的部分减少到m比特。也就是说，当m被l(r_k)代替时，L_agv=m。这样当图像的灰度级使用自然二进制码编码时，代码冗余几乎总是存在的。

你会很自然的提出如下问题：表示一幅图像的灰度级的灰度级到底需要多少比特？也就是说，是否存在不丢失信息的条件下，能足够充分描绘一幅图像的最小数据量？信息论提供了回答这一问题的数学框架。基本前提是信息的产生可用概率过程来建立模型，这个过程可以用与直觉相符的方式来度量。为了与这个假定相一致，概率为P(E)的随机事件E包含了下面这样的信息单位：$$I(E)=\log \frac{1}{P(E)}=-\log P(E)$$如果P(E)=1（也就是说，这个事件总会发生），那么I(E)=0，也就是没有信息。换句话说，因为没有与这个事件关联的不确定因素，所以也就没有事件已发生需要传递的信息。在离散的可能事件的几何｛a₁,a₂,…,a_J｝中给定随机始建于，与之相关的概率为｛P(a₁),P(a₂),…,P(a_J)｝，每个输出信源的平均信息被称为信源的熵：$$H=-\sum _{k=1}^{L}P(a_j)\log P(a_j)$$如果一幅图像可被看做发出自身“灰度级信息源”的样本，就可以用被观测图像的灰度级直方图来对信源符号概率建模，并生成被称为一阶估计的H^~，也就是信源的熵：$$\hat{H}=-\sum _{k=1}^L{p}_r(r_k)\log p_r(r_k)$$我们来简单计算一下4×4图像的熵：

function h = ntrop( x, n )

error(nargchk(1, 2, nargin));
if nargin < 2;
    n = 256;
end

x = double(x);
xh = hist(x(:), n);
xh = xh / sum(xh(:));

i = find(xh);

h = -sum(xh(i) .* log2(xh(i)));

end

>> f = [119 123 168 119; 123 119 168 168];
>> f = [f; 119 119 107 119; 107 107 119 119];
>> f

f =

   119   123   168   119
   123   119   168   168
   119   119   107   119
   107   107   119   119

>> p = hist(f(:),8);
>> p = p / sum(p)

p =

    0.1875    0.5000    0.1250         0         0         0         0    0.1875

>> h = ntrop(f)

h =

    1.7806

2.1 霍夫曼码

当对一幅图像的灰度级或某个灰度级映射操作的输出进行编码时（像素差、行程长度，等等），霍夫曼码包含了对于每个信源符号（比如灰度值）可能的最小编码符号（如比特）数，遵从每次仅编码一个信源符号的限制条件。

霍夫曼编码的第一步是通过对符号的概率进行排序，建立信源递减序列，这种符号排序考虑了合并最低概率的符号作为单独的符号，并在下一次信源约简时替换他们。

霍夫曼编码过程的第二步是对每个约简的信源进行编码，编码从最小的信源开始，一直到原始信源。当然，对于两符号信源的最短二进制编码由0和1组成。

霍夫曼编码是瞬时的、唯一可译码的块编码。之所以是块编码，是因为每个信源符号均映射到固定的码字符号序列。之所以是瞬时的，是因为码字符号字符串的每个码字可以不参照随后的符号而被译码。也就是说，在任意给定的霍夫曼码中，没有码字是其他码字的前缀。之所以是唯一可译码的，是因为代码符号字符串仅有唯一的译码方法。下面我们来实现以下信号约简和代码分配的过程：

function CODE =huffman(p) 
error(nargchk(1,1,nargin));
if (~ismatrix(p)) ||(min(size(p))>1)||~isreal(p)||~isnumeric(p)
   error('P must be a real numeric vector.'); 
end 
global CODE
CODE=cell(length(p),1);
if length(p)>1
    p=p/sum(p);
    s=reduce(p);
    makecode(s,[]);
else
    CODE={'1'};
end

function s = reduce(p)
s=cell(length(p),1);
for i=1:length(p)
    s{i}=i;
end
while numel(s)>2
    [p,i]=sort(p);
    p(2)=p(1)+p(2);
    p(1)=[ ];
    s=s(i);
    s{2}={s{1},s{2}};
    s(1)=[ ];
end

function makecode(sc,codeword)
global CODE
if isa(sc,'cell')
    makecode(sc{1},[codeword 0]);
    makecode(sc{2},[codeword 1]);
else
    CODE{sc}=char('0'+codeword);
end

>> p = [0.1875 0.5 0.125 0.1875];
>> c = huffman(p)

c = 

    '011'
    '1'
    '010'
    '00'

输出是长度可变的字符数组，其中的每一行是由0和 1(对应索引符号 P中的二进制码)组成的字符串。例如，‘010’是概率为0.125的灰度级的码字。

2.2 霍夫曼编码

霍夫曼码的产生不是压缩过程（在自身内部）。为了实现成为霍夫曼码的压缩，对于产生码字的符号，不管它们是灰度级、行程长度，还是其他灰度映射操作的输出，都必须在生成码字一致的情况下被变换或映射，下面是MATLAB中的变长编码映射：

考虑简单的16字节4×4图像：

>> f2 = uint8([2 3 4 2; 3 2 4 4; 2 2 1 2; 1 1 2 2])

f2 =

    2    3    4    2
    3    2    4    4
    2    2    1    2
    1    1    2    2

>> whos('f2')
  Name      Size            Bytes  Class    Attributes

  f2        4x4                16  uint8        

f2中的每个像素都是8比特的字节，16字节用于表现整幅图像，因为f2的灰度不是等概率的，所以变长码字会减少表现图像所必须的存储量。使用函数Huffman计算码字：

>> c = huffman(hist(double (f2 (:)), 4))

c = 

    '011'
    '1'
    '010'
    '00'

因为霍夫曼码与被编码的信源符号出现的频率有关(不是信号本身)，所以 C 和例 8.1 中构成图像的码字一样。事实上，图像 f2 可以从例 8.1 中分别把灰度级107、119、123 和 168 映射到 1、2、3、4 来得到。对于任何一幅图像，p = [ 0.1875 0.5 0.125 0.1875]。

基于码字 c 对 f2 编码的简单方法是执行如下简单的查表操作：

>> h1f2 = c(f2(:))'

h1f2 = 

  1 至 11 列

    '1'    '010'    '1'    '011'    '010'    '1'    '1'    '011'    '00'    '00'    '011'

  12 至 16 列

    '1'    '1'    '00'    '1'    '1'

>> whos('h1f2')
  Name      Size            Bytes  Class    Attributes

  h1f2      1x16             1850  cell        

这里，f2(UNIT8 类的二维数组)被变换成单元数组 hlf2 转置的紧凑显示。hlf2 中的元 素是可变长度的字符串，并对应 f2 中从上到下、从左到右扫描的像素(也就是列方式)。正如看到的那样，被编码的图像用了存储的 1018 个字节，基本上是f2要求的存储量的 60倍。

对 hlf2 使用的单元数组是合乎逻辑的，因为这是处理不同数据的两个标准 MATLAB 数据结构之一。对于 hlf2，不同之处在于字符串的长度，以及为通过单元数组透明 地处理它所付出的代价是存储器的总开销(单元数组固有的特性)，要求必须追踪变长元素的位置。可以通过把 hlf2 变换为两维的字符数组来减少此开销。

>> h2f2 = char(h1f2)'

h2f2 =

1010011000011011
 1 11  1001  0  
 0 10  1  1     

>> whos('h2f2')
  Name      Size            Bytes  Class    Attributes

  h2f2      3x16               96  char      

在这里，单元数组 hlf2 被变换为 3x16 的字符数组 h2f2。h2f2 的每一列以从上到下、 从左到右扫描方式对应 f2 中的像素，也就是列方式)。注意，空白处被以合适的尺寸插入数组， 并且因为对于码字的 0 和 1 都要求两字节，所以 h2f2 的存储总量是96 字节，还是比 f2 需要 的原始 16 字节大6倍。可以像下面这样来消除插入的空格：

>> h2f2 = h2f2(:);
>> h2f2(h2f2 == ' ') = [];
>> whos('h2f2')
  Name       Size            Bytes  Class    Attributes

  h2f2      29x1                58  char  

但是要求的存储空间还是比f2的原始16字节要大，为了压缩f2，码字c必须在比特级应用，用一些编码像素打包成单字节：

>> h3f2 = mat2huff(f2)

h3f2 = 
    size: [4 4]
     min: 32769
    hist: [3 8 2 3]
    code: [43867 1944]

>> whos('h3f2')
  Name      Size            Bytes  Class     Attributes

  h3f2      1x1               726  struct          

虽然 mat2huff 函数返回结构 h3f2, 但仍要求 726 个字节的存储量，其中大部分开销都和下面两个因素有关： 1)结构可变的开销MATLAB 中的每个 结构字段需要 124 个字节的开销) ;2) mat2huff 产生的信息更易于将来的译码。忽视这些开销， 当考虑实际(比如普通大小)的图像时，它们是可以忽略掉的。mat2huff 以 4:1 的比率压缩 f 2。f2 的 16 个 8比特像素被压缩为两个16比特的字 h3f2 中字段 code 的元素:

>> hcode = h3f2.code;
>> whos('hcode')
  Name       Size            Bytes  Class     Attributes

  hcode      1x2                 4  uint16              

>> dec2bin(double(hcode))

ans =

1010101101011011
0000011110011000

注意，dec2bin 被用来显示 h3f2.code的单比特。忽视末尾的模 16 的插入比特(最后的 3 个 0)，32 比特编码相当于先前产生的、瞬时且唯一的、可解码的 29 比特码字10101011010110110000011110011。

这里我放入mat2huff函数的源码：

function y = mat2huff(x)
%MAT2HUFF Huffman encodes a matrix.
%   Y = MAT2HUFF(X) Huffman encodes matrix X using symbol
%   probabilities in unit-width histogram bins between X's minimum
%   and maximum values. The encoded data is returned as a structure
%   Y: 
%      Y.code   The Huffman-encoded values of X, stored in
%               a uint16 vector.  The other fields of Y contain
%               additional decoding information, including:
%      Y.min    The minimum value of X plus 32768
%      Y.size   The size of X
%      Y.hist   The histogram of X
%
%   If X is logical, uint8, uint16, uint32, int8, int16, or double,
%   with integer values, it can be input directly to MAT2HUFF. The
%   minimum value of X must be representable as an int16.  
%
%   If X is double with non-integer values---for example, an image
%   with values between 0 and 1---first scale X to an appropriate
%   integer range before the call. For example, use Y =
%   MAT2HUFF(255*X) for 256 gray level encoding.   
%
%   NOTE: The number of Huffman code words is round(max(X(:))) -
%   round(min(X(:))) + 1.  You may need to scale input X to generate
%   codes of reasonable length.  The maximum row or column dimension
%   of X is 65535. 
%
%   See also HUFF2MAT.
%   Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins
%   Digital Image Processing Using MATLAB, Prentice-Hall, 2004
%   $Revision: 1.5 $  $Date: 2003/11/21 15:21:12 $
if ndims(x) ~= 2 | ~isreal(x) | (~isnumeric(x) & ~islogical(x))
   error('X must be a 2-D real numeric or logical matrix.');
end
% Store the size of input x.
y.size = uint32(size(x));
% Find the range of x values and store its minimum value biased
% by +32768 as a UINT16.
x = round(double(x));
xmin = min(x(:));
xmax = max(x(:));
pmin = double(int16(xmin));
pmin = uint16(pmin + 32768);    y.min = pmin;
% Compute the input histogram between xmin and xmax with unit
% width bins, scale to UINT16, and store.
x = x(:)';
h = histc(x, xmin:xmax);
if max(h) > 65535
    h = 65535 * h / max(h);
end
h = uint16(h);   y.hist = h;
% Code the input matrix and store the result.
map = huffman(double(h));          % Make Huffman code map
hx = map(x(:) - xmin + 1);         % Map image
hx = char(hx)';                    % Convert to char array
hx = hx(:)';
hx(hx == ' ') = [];                % Remove blanks
ysize = ceil(length(hx) / 16);     % Compute encoded size
hx16 = repmat('0', 1, ysize * 16); % Pre-allocate modulo-16 vector
hx16(1:length(hx)) = hx;           % Make hx modulo-16 in length
hx16 = reshape(hx16, 16, ysize);   % Reshape to 16-character words
hx16 = hx16' - '0';                % Convert binary string to decimal
twos = pow2(15:-1:0);
y.code = uint16(sum(hx16 .* twos(ones(ysize, 1), :), 2))';

2.3 霍夫曼译码

霍夫曼编码图像几乎没什么用，除非能被解码并重建为刚开始时的原始图像。前面一节的输出 y = mat2huff (x) ，解码器必须首先计算用来编码 x 的霍夫曼码(基于 x 的直方图 和 y 中有关的信息)，然后反映射已编码的数据(还是从 y 中提取)来重建 x。

正如在下面列出的函数 x=huff2mat (y) 中看到的那样，上述处理可以分为 5 个基本步骤:
(1) 从输入结构 y 中提取维数 m 和 n，以及最小值 xmin(最后的输出 x)。
(2) 重新创建霍夫曼码，通过将它的直方图传递到 huffman 函数来对 x 进行编码。在列 表中产生的编码将被map 调用。
(3) 建立数据结构(转换和输出表 link), 以便在 y.code 中通过一系列有效的二进制搜索 对编码数据解码。
(4) 传递数据结构和已编码数据(比如 link 和 y.code)到 C 函数 unravel。这个函数最 小化为执行二进制搜索要求的时间，产生已解码的 double 类的输出向量 X。
(5) 把xmin添加到x的每个元素中，并加以改造以匹配原始x的维数(也就是m行和n列)。

huff2mat 的唯一特点是对 MATLAB 可调用C 函数 unravel 的结合，这使得对大多数标准分辨率的图像的解码几乎都是瞬时的。这里由于要使用matlab结合c语言就不作解码的展示了。

3 空间冗余

空间冗余：图像内部相邻像素之间存在较强的相关性多造成的冗余。

>> f1 = imread('Fig1135(a).tif');
>> f2 = imread('Fig1135(b).tif');
>> subplot(2,2,1),imshow(f1),title('(a)Original Image');
>> subplot(2,2,2),imhist(f1),title('(b)Hist Of Image A');
>> subplot(2,2,3),imshow(f2),title('(c)Original Image');
>> subplot(2,2,4),imhist(f2),title('(b)Hist Of Image B');

>> c1 = mat2huff(f1);
>> ntrop(f1)
ans =

    7.4254

>> imratio(f1, c1)

ans =

    1.0707
    
>> c2 = mat2huff(f2);
>> ntrop(f2)
ans =

    7.3463

>> imratio(f2, c2)

ans =

    1.0830

注意，这两幅图像的一阶熵估计大致相同(分别为7.4254和 7.3463 比特/像素)；它们同样由 mat2huff 压缩(压缩比为 1.0707 和 1.0830)。这些明显强调了如下事实：变长编码的设计不是为了利用上图B中排成一排的火柴之间的明显结构关系的优点。虽然在图像中，像素与像素之间的相关性更明显，但这一现象在上图A中也存在。因为任何一幅图中的像素都可以合理地从 它们的相邻像素值预测，这些单独像素携带的信息相对较少。单一像素的视觉贡献对一幅图像 来说大部分是多余的；它们应该能够在相邻像素值的基础上推测出来。这些相关性是像素间冗余的潜在基础。

为了减少像素间的冗余，通常必须把由人观察和解释的二维像素数组变换为更有效的格式 (但通常是“不可视的”） 。例如，邻近像素点之间的差值可以用来表示一幅图像。这种类型(也就是说，移走像素间的冗余)的变换被称为映射。如果原始图像可以从变换的数据集重建，它们就被称为可逆映射。 下图展示了简单的映射过程(图中的X_k等同于f_n)。这种被称为无损预测编码的处理方法可以通过对每个像素中新的信息进行提取和编码来消除相近像素间的冗余。像素的新信息被定义为实际值和预测值 的差值。由此可见，系统由编码器和解码器组成，每个都含有相同的预测器。当每个输入图像 中相继的像素表示为f_n时，f_n被送进编码器，预测器以过去某些输入为基础产生像素的预测值。 预测器的输出被四舍五入成最接近的整数。表示为f^_n; 并用来产生差或预测误差：$$e_n=f_n-{\hat{f}}_n$$

预测误差用变长编码（通过符号编码器）产生压缩数据流的下一个元素。上图中接收端的解码器用收到的变长码字执行相反的操作以重建e_n：$$f_n=e_n+{\hat{f}}_n$$各种本地的、全局的和自适应方法可以用来产生f^_n。然而对于大部分情况，预测由前面的几个像素的线性结合而形成，也就是：$$\widehat{f_n}=round[\sum _{i=1}^m{\alpha }_i{f}_{n-i}]$$这里，m是线性预测器的阶，“round”是用来表示四舍五入或接近整数的函数。并且a_i对于i=1,2,…,m是预测参数。对于一维线性预测编码，这个等式可以写作：$$\hat{f}(x,y)=round[\sum _{i=1}^m{\alpha }_{i}f(x,y-i)]$$这里，每个带下标的变量已明确作为空间坐标（x，y）的函数来表示。注意预测f（x，y）是当前的扫描行上前一些像素的函数。下面实现无损预测编码：

f=imread('Fig1135(b).tif');
subplot(1, 3, 1);imshow(f);
title('(a)Original Image')
fshang=entropy(f)          
c0=mat2huff(double(f));
cfshang=entropy(c0.code)   
cfr=imratio(f,c0)          
e=mat2lpc(f);
subplot(1, 3, 2),imshow(mat2gray(e));
title('(b)Image After Linear Prediction Coding');
esgang=entropy(e)          
cer=imratio(f,e)%cer=1.0821
c=mat2huff(e);             
ceshang=entropy(c.code)    
cr=imratio(f,c)           
[h,x]=hist(e(:)*512,512);
subplot(1, 3, 3),bar(x,h,'k');title('(c)Prediction error histogram');

注意，0周围的峰值很高，与输入图像的灰度级务布相比有相对较小的方差。 这反映出正如前面计算的熵值那样，由预测和微分处理移去了大量的像素间冗余。

4 不相关的信息

与编码及像素间冗余不同，心理视觉冗余和真实的或可计量的视觉信息有联系。心理视觉冗余的去除是值得的，因为对通常的视觉处理来说，信息本身不是本质的。因为心理视觉冗余数据的消除引起的定量信息损失很小，所以称为量化。这个术语和普通词的用法一样。通常意味着把宽范围的输入值映射为有限数量的输出值。这是不可逆操作(也就是说，视觉信息有损失)，量化将导致数据的有损压缩。下面仅使用了IGS量化的无损预测和霍夫曼编码

>> f = imread('raccoon.jpg');
>> f = rgb2gray(f);
>> q = quantize(f,4,'igs');
>> qs = double(q) / 16;
>> e = mat2lpc(qs);
>> c = mat2huff(e);
>> imratio(f,c)

ans =

    3.7075

已编码的结果c可以通过相反的操作来解压缩（不用进行反量化）：

>> ne = huff2mat(c);
>> nqs = lpc2mat(ne);
>> nq = 16 * nqs;
>> compare(q,nq)
ans =
    0
>> compare(f,nq)
ans = 
    6.8382

注意，解压缩图像的均方根误差大约是7个灰度级，这个误差源于量化步骤。

5 JPEG压缩

5.1 JPEG

最流行且综合的连续色调的静止画面压缩标准之一就是JPEG（Joint Photographic Experts Group）。JPEG基本编码标准是基于离散余弦变换的，在大多数压缩应用中已足够满足需要，输入和输出都被限制在8比特，量化为DCT系数值时限制为11比特。正如在下图中看到的那样，压缩本身分4步执行：8×8子图像抽取，DCT计算，量化和变长编码分配。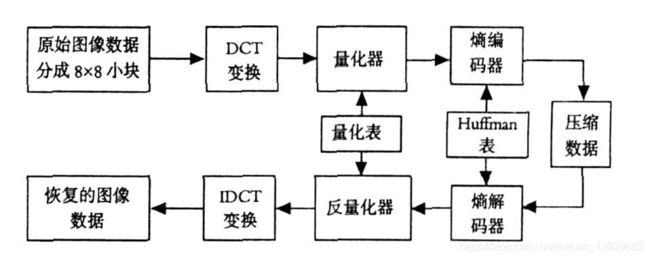
JPEG压缩处理的第一步是把输入图像细分为不相重叠的8×8大小的像素块。它们随后被从左到右、从上到下进行处理。当每个8×8像素块或子图像都被处理后，像素块的64个像素就通过减去2^m-1进行量级移动。这里，2^m是图像的灰度级数，并且计算图像的二维离散余弦变换。然后，得到的系数根据下式进行归一化和量化：$$\hat{T}(u,v)=round[\frac{T(u,v)}{Z(u,v)}]$$其中，u,v=0,1,…,7是去归一化结果和量化的系数，T(u,v)是图像f(x,y)的8×8像素块的DCT，Z(u,v)是默认的JPEG归一化数组。通过标定Z(u,v)，可以得到各种压缩比率和重建图像的质量。JPEG标准的全部实现已超出本章范围，这里仅仅了解方法。

5.2 JPEG 2000

虽然JPEG标准是一个非常成功的标准，但在一些新的应用如高清图像、数字图书馆、高精确彩色图像、多媒体和因特网应用、无线、医学图像等方面，JPEG表现不足，因此弥补JPEG对连续色调静止图像的无损压缩和近无损压缩效率不高的缺陷，最终提出了JPEG2000标准。

该标准采用了先进的压缩技术并在可伸缩压缩图像及灵活性方面有许多先进的特征，其系统功能比JPEG标准优越，尤其是JPEG2000采用的是离散小波变换替代了JPEG中采用的离散余弦变换，并采用了最新的编码算法来支持灵活性，这样许多应用只需要单一码流提供。JPEG2000可广泛应用于通信、图像处理、信号处理和多媒体 等领域中。

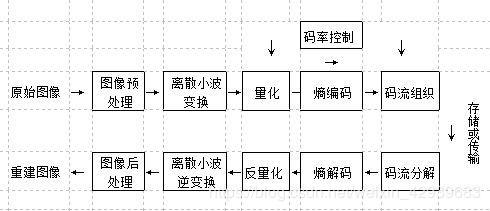
JPEG2000与传统JPEG最大的不同在于它放弃了JPEG所采用的以离散余弦为主的区块编码方式，转而采用以小波变换为主的多解析编码方式。

余弦变换是经典的谱分析工具，它考察的是整个时域过程的频域特征或整个频域过程的时域特征，因此对于平稳过程，它有很好的效果，但对于非平稳过程，它却有诸多不足。图像的压缩率越高，频域信息被丢弃的越多。

小波变换是现代谱分析工具，它既能考察局部时域过程的频域特征，又能考察局部频域过程的时域特征，因此即使对于非平稳过程，处理起来也得心应手。它能将图像变换为一系列小波系数，这些系数可以被高效压缩和存储。此外，小波的粗略边缘可以更好的表现图像，因为它消除了DCT压缩普遍具有的方块效应。通过伸缩平移运算对信号逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节。