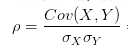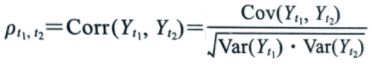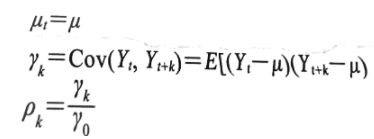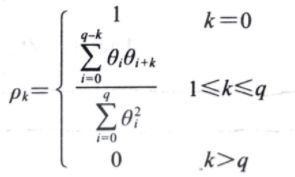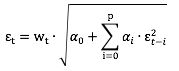R语言实现时间序列分析

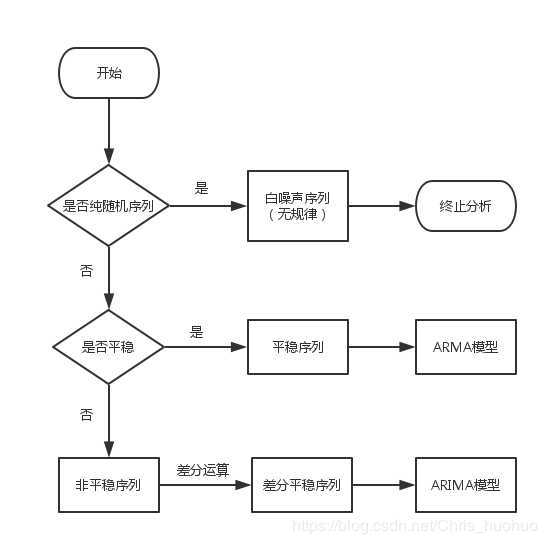
一、时间序列分析导论图：

处理方式：

      1.对于原始数据进行季节性处理和差分，以形成平稳序列；期间如果遇到了随机序列，则停止时间序列建模

      2.对于给定的序列进行自相关函数和偏自相关函数分析（在不同的滞后k值下的值），绘制自相关函数图和偏自相关函数图，看是否是AR、MA或ARMA模型

      AR(p)模型对应的偏自相关函数是以p步截尾的，对应的自相关函数是拖尾的，呈正弦波（或指数衰减）并趋于0

      MA(q)模型对应的自相关函数是以q步截尾的，对应的偏自相关函数是拖尾的，呈正弦波（或指数衰减）并趋于0

      ARMA(p,q)模型对应的自相关函数和偏自相关函数都是截尾的

      3.判定好AR、MA或ARMA模型后，去寻找p和q值

二、时间序列基本概念：

      时间序列：对于一个变量Y在不同时间点上的取值Y1、Y2……YT的一个序列，它的索引是等间距的时间点序列

      随机过程：由一种随机机制（和确定性机制相反）所产生的一个随机变量的序列

      时间步骤：当我们说道时间步骤t时，就是指的，在已有的时间序列和它的等间距时间差之间，按照这个时间差第t个时间索引所对应的变量值

三、时间序列的摘要函数：

      首先，我们将时间序列中时间里的每个点视作一个随机变量，且该时间序列在某个时间索引t上的值是Yt

均值函数：某个时间序列在某个时间索引t上的期望值：

协方差：描述两个变量变化的相似程度。

        你变大，同时我也变大，说明两个变量是同向变化的，这时协方差就是正的。

        你变大，同时我变小，说明两个变量是反向变化的，这时协方差就是负的。

        协方差的数值越大，两个变量同向程度也就越大。反之亦然。

       

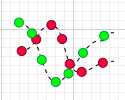
       很多时候X，Y的运动是不规律的，比如：

                                            

                                            

            这时，很可能某一时刻的值与的值乘积为正，另外一个时刻的值与的值乘积为负。

            将每一时刻与的乘积加在一起，其中的正负项就会抵消掉，最后求平均得出的值就是协方差，通过

            协方差的数值大小，就可以判断这两个变量同向或反向的程度了。

相关系数：一种剔除了两个变量量纲影响、标准化后的特殊协方差

• • 反映两个变量变化时是同向还是反向，如果同向变化就为正，反向变化就为负。

  • 它消除了两个变量变化幅度的影响，而只是单纯反应两个变量每单位变化时的相似程度。

  • 反应的就是两个变量每单位变化时的情况。

  • 只能在＋1到－1之间变化

  • 当变量X与Y的相关系数为1时，说明两个变量变化时的正向相似度最大，即，你变大一倍，我也变大一倍；你变小一倍，我也变小一倍。也即是完全正相关，呈线性关系

  • 当变量X与Y的相关系数为0时，两个变量的变化过程没有任何相似度，也即两个变量无关。

  • 当变量X与Y的相关系数为－1时，说明两个变量变化的反向相似度最大，即，你变大一倍，我变小一倍；你变小一倍，我变大一倍。也即是完全负相关，呈线性关系

标准差：——描述了变量在整体变化过程中偏离均值的幅度

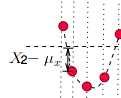
            每一时刻变量值与变量均值之差再平方，求得一个数值，再将每一时刻这个数值相加后求平均，再开方。其中是偏离均值的幅度；做平方的原因是因为有时候变量值与均值是反向偏离的（见下图），是个负数，平方后，就可以把负号消除了。这样在后面求平均时，每一项数值才不会被正负抵消掉，最后求出的平均值才能更好的体现出每次变化偏离均值的情况；最后又开平方的原因是因为刚才为了消除负号影响，取了一次平方，最后肯定要把求出的均值开方，将这个偏离均值的幅度还原回原来的量级。

自协方差函数：——衡量时间序列中的随机变量在不同时间点上相互的线性依赖性   

 

                当两个时间索引相同时，自协方差函数就是方差：

 

• 单位是原始时间序列的随机变量的平方，并且自协方差函数是对称的，转换t1和t2的位置其值不变

自相关函数（ACF函数）——衡量时间序列中的随机变量在不同时间点上相互的线性依赖性

 

• 自相关函数是对称的，转换t1和t2的位置其值不变；无单位，取值在-1到+1之间，+1和-1时为完全线性依赖，0时为在这两个时间索引下的变量值无关
• 当用在两个相等的时间索引对应变量上时，值为1

三、基本的时间序列

1.白噪声

      白噪声（离散白噪声）：在一个白噪声时间序列中，产生出来的随机变量都是具有均值0和有限且相等的方差，并且不同时间步骤的随机变量是互相之间不相关的。同时也要求独立同分布（IID）

      IID（独立同分布）:要求每个随机变量来自于完全相同的分布，例如某个均值和标准差都相同的正态分布；要求来自不同时间序列步骤的两个变量不仅互相不相关，而且还是独立的。

      ps：两个相互独立的变量必然不相关，但是两个不相关的变量不一定相互独立

      高斯白噪声：从正态分布中抽取的白噪声时间序列

      构建白噪声时间序列模型关键变量：方差

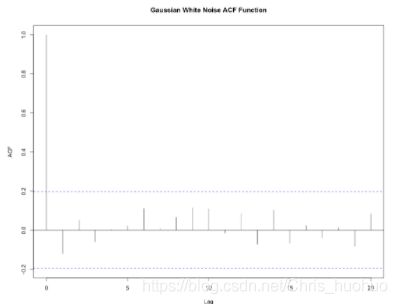
      白噪声时间序列的显著性检验：

      运用R语言中acf（）函数绘制相关图，本方法是对于步长为k的时间步骤的配对进行估算。其中结果的横轴为k（延迟）的不同值，纵轴为ACF函数的值，虚线为在给定的例如95%置信区间下，对应的ACF值最大值（超过这个就认为是显著了，没有发现超过的话，则认为不具有统计显著性），结果中所有的k=0时都会对应一个ACF值，为1（相当于对于一个k=n而言，会取原点的变量值和与它相隔n个时间间隔的变量值去求ACF函数值）。由于抽样的偏误性，ACF函数在不同的k值上应该不会正好为0.

2.随机漫步

      随机漫步的时间序列：指某一个时间序列的某一变量在连续时间点之间的差异是白噪声

      前提条件：

      规定递归关系：

      首先，递归关系是指这个时间序列中，每一个时间步骤上的某个变量值都会被定义为这个时间序列上之前的时间步骤上这个变量的值和某个增量的函数（如第一个函数）；其次，规定一个该时间序列第一个项的初始状态值

      这里，第一个方程规定了在指定的时间步骤为t的某个变量的值上，通过加入项，来跟他往后措一个时间步骤的这个变量的值产生联动；第二个方程规定了该随机漫步时间序列的起始条件（即第一个项）是一个白噪声序列的第一个项。

• • 根据一个并行的白噪声序列产生的每一个单个的正或负的数值（即白噪声时间序列中的项）对于它自己的当前值进行调整的一种序列

  • 在时间步骤t，随机漫步的对应项实际就是t个均值为0，方差都为独立同分布变量之和，这些变量都是白噪声序列的项。可以推断随机漫步（不带有漂移的随机漫步序列）的均值函数对于所有的时间点都是0，方差是t✖️得出，故方差会随着时间序列的增长而变大

      构造随机漫步：

      对一个白噪声随机序列进行累计求和，利用R语言cumsum（）函数来做

      拟合随机漫步：

      计算所给的时间序列的连续差值，用R语言的diff（）函数；再用白噪声检测去检验，只要符合白噪声序列就可以推断为随机漫步。

      带有漂移的随机漫步序列：

      在Yt和Yt-1的差值上，给序列中的每个点加上了一个常数项a，这个常数项a被称作为漂移。若我们先得到一个随机漫步，把它改作一个带有漂移项的随机漫步，那么改变后的序列的方差和改变之前是相同的，但是改变之后的序列的均值是实时变化的，为t*a五、平稳性假设

      1.几个概率的区分：

      联合概率：在多元的概率分布中多个随机变量分别满足各自条件的概率。假设X和Y都服从正态分布，那么P{X<4,Y<0}就是一个联合概率，表示X<4,Y<0两个条件同时成立的概率。表示两个事件共同发生的概率。A与B的联合概率表示为 P(AB) 或者P(A,B),或者P（A∩B）。

      边缘概率：是某个事件发生的概率，而与其它事件无关。

      条件概率：指事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为：P（A|B），读作“在B条件下A的概率”。

      2.时间序列预测建模假设：

      平稳性假设：一个时间序列的概率表现不会随着时间的流逝而改变，即对时间平移的不变性做了假设——重要但有限制性的假设（即对同一个小的时间段内，不能时间往后推移了，这个小的时间段的变化就出现天壤之别）

      严格平稳（强平稳）：（即在一个时间长河中，对于同一个小的时间段，它的变化幅度需要一模一样，不管这个时间段大小如何）

      从时间t起始的一个点序列的联合概率分布和从时间T起始的另一个点时间列的联合概率分布相同，其中T=t+k。在这里，我们的n指的是所有可能的一个时间间隔；k指的是时间延迟，说明在整个时间推移上这个规律都是通用的。

      当我们选择极端情况n=1时，说明序列中每个点的概率分布都是相同的（单变量概率），证明了在一个严格平稳的时间序列中，均值函数是不随时间变化的常数，方差也是不随时间变化的常数。

      但这个在现实中很难实现，不好验证。

      弱平衡：（平稳随机过程、平稳时间序列）（即在一个时间长河中，对于同一个小的时间段，它的变化幅度总体是趋向一个标准的，但是允许对于不同的时间段出现不同的波动）

      均值函数是常数函数，不随时间变化；协方差函数仅与时间差相关，依赖于序列中两点之间的时间延迟。表示为，其中表示为时间步骤为t+k与时间步骤为t所形成的时间段的变化幅度。

      说白了，不管是严格平衡还是弱平衡都要求对于指定的时间段，在时间长河上的这个段内的差异表现（均值）是相同的，只不过严格平衡还要求不管这个时间段取多大，他们所体现出来的协方差还要相同（统一的）；而弱平衡只要求每个具体的时间段在时间长河上所体现的方差是相同的就好，意味着不同的时间段k体现出的协方差可以是不同的

3.平稳时间序列

      平稳时间序列的均值函数、自协方差和自相关性如下：

      其中延迟为0的自协方差（即）就是方差。

      白噪声是一个平稳过程（强平稳），他的均值是一个常数，方差也是一个常数；随机漫步的均值是常数（带有漂移的随机漫步并不是）但是方差是随着时间的变化而不同的，它是不平稳的

六、平稳时间序列模型

1.移动平均模型MA

• 模型建立

      移动平均MA过程是一个随机过程，其中在时间步骤t的随机变量是一个白噪声过程的（时间上）最近的项（具体到最近的哪几项这个值为q）的线性组合，表示如下，其中q是这个时间步骤t能用前面的几项来描述，为系数（常数值）：

或者是，其中相当于是线性关系中的常数项，加不加都行，且e表示的各项是均值为0、方差为的白噪声随机变量。

      对上一个式子进行改进，以用这个量去表示时间步骤t的变量值，引入后算因子这个概念，当后算因子用于一个随机过程中在时间t的随机变量时，会产生前一个时间步骤t-1的随机变量，如下：

      通过这样，可以通过连续用后算因子来获得时间更早的随机变量，我们可以看出，代表运用后移算子两次即后移了两个时间步骤。最终以用这个量去表示时间步骤t的变量值，改造成：

                                     (这里默认了为1)

      这个包含了一个后移算子B的 q阶多项式称作MA过程的特征多项式，如下：

      这里我们首先将后移算子B换成了x，不管MA过程的系数或者阶数q如何选择，他都会是平稳的（因为e是一个白噪声序列）。回到特征多项式上，对于这个多项式的根，如果绝对值大于1，那么这个MA过程称作是可逆的，一个ACF图对应的可逆MA过程是唯一的，但是这个ACF图对应的不可逆MA过程则不是唯一的。

• 统计学性质：

      由于每个e项都是一个白噪声随机变量，所以MA过程的均值恒为0，方差如下（是一个常数），我们定义为1（这么做纯粹是为了写出后面的求和公式）(这个公式也说明，向前推q个过程的q不影响整个时间序列的均值，但是印象它的方差)

      由于MA过程的阶数是通过自相关函数求的，于是将自相关函数给出如下：

      核心是MA过程的ACF（自相关函数）对于小于该过程的阶数q的延迟是非0值，之后就都等于0（这里涉及到一个显著性问题，所以在图上如果都在虚线内就认为是0了）（用人话来讲，就是先做出MA过程关于延迟的ACF函数，找到在某个k值之前的ACF函数值都是非0值但是之后的都是0值的，这个k值就是q的取值）这个过程用于判别MA过程（画ACF看看到底能不能用MA模型）并且估算MA过程的阶数（确定MA模型之后看它的阶数q是多少是有用的），在这里，我们把具有统计学显著性的非0值得最大延迟数作为它的阶数

      R语言中经常用arima.sim()函数模拟MA（和其他过程）过程，指定n参数为序列的长度（时间区间的长度），model参数为要模拟的序列的参数（包括ma属性中设置了系数的取值，是一个向量，sd属性中设置了白噪声项的标准差（即e的标准差））。这个函数的返回值中ts（一个特殊的时间序列对象）包括了模拟结果，用来追踪一个时间序列的某些基本信息和支持专门用于时间序列分析的绘图。

2.自回归模型AR

• 模型建立

      自回归模型AR源自让一个简单的模型根据过去有限窗口时间里（也就是说，我们站在时间步骤t上，看看之前的窗口（如果是p）内包含的p个时间步骤的值，如何去解释现在时间步骤t的值）解释某个时间序列当前值的想法。一个p阶AR模型的方程是：

或，其中可以看做是线性关系中的常数项。

      再次引入后移算子这个东西，变成用这个量去表示时间步骤t的变量值，得到：

或    （这里默认了为1）

      与MA不同，AR不一定总是平稳的，先看AR的特征方程（其中还是用x换掉了B）：

或

      当且仅当方程的根都大于1，AR过程才是平稳的。方程的根都大于1的必要（非充分条件）为：

      这个AR的特征方程经常用来发现非平稳的AR过程，例如随机漫步就是非平稳的，因为第一个系数就是1

• 统计学性质

      AR没有像MA过程里的那种所有大于MA过程阶数q的延迟值对应的ACF都是0的分段性质，它的ACF更体现出一种指数型衰减（不像MA那种一下掉下来（显著性为0的带子里）），所以我们改用偏自相关函数PACF图去看。时间延迟k的偏自相关定义为在消除了小于k的延迟中存在的任何相关性影响下所产生的相关性，即p阶AR过程仅仅依赖于过去恰好p个单位时间的过程的值。

      判断方法：对于所有大于p的延迟，PACF图会出现0值，把PACF延迟项k呈现了统计学显著性（非0值）的最大时间延迟数（即在这个最大的k值前不出现统计学显著性非0值）当做AR过程的阶数。

3.自回归移动平均模型ARMA

      把移动平均和自回归模型合并成一个兼具移动平均过程和自回归模型的元素的模型，定义为移动平均自回归ARMA模型。一个ARMA(p，q)过程（具有p阶自回归项和q阶移动平均项的ARMA过程）的一般方程如下：

      其中我们默认了和这种常数项就不考虑了。

      一个纯移动平均过程MA(q)可以写成ARMA过程ARMA(0，q)

      一个纯自回归过程AR(p)可以写成ARMA过程ARMA(p，0)

      ARMA过程平稳的前提是在它的AR成分的特征方程（即）存在绝对值大于1的根

      ARMA过程是可逆的前提是在它的MA成分特征方程（即）存在绝对值大于1的根

      ARMA过程是唯一的前提是MA和AR成分的特征方程没有共同的因式，因为共同的因式会互相抵消，让我们得到一个相等的但更低阶的ARMA过程

4.ARMA、AR、MA过程的处理过程（以ARMA为例）：

      第一，通过找出p和q来判别ARMA过程的阶数

      第二，尝试估算AR和MA成分的系数值（即和）——可以通过观测到的序列和估算的序列之间误差平方和最小化去卡这个系数值，或者通过AIC去判断

八、非平稳时间序列模型

      解决的方案要不就是从原始数据上派生出一个平稳模型，要不就是对它的非平稳表现进行建模

1.基础概念：

      差值序列：对于原始序列而言，通过求解连续点Yt和Yt+1之间的差DYt，构成了一个新的时间序列模型

      二阶差值序列：对于差值序列，再次对于它的连续点取差值，得到的那个序列叫做二阶连续差值

      d阶差值：通过重复d次计算连续项的差值，从某个原始序列Yt得到一个新的点序列Wt，方程为：

2.ARIMA模型：

      ARIMA模型（整合自回归移动平均过程）：组成这个时间序列的项是d阶差值Wt，这个d阶差值是一个平稳的ARMA过程。一个ARIMA(p,d,q)过程要求d阶差值，具有q阶的MA成分，以及p阶的AR成分。一个普通的ARMA(p,q)过程就等于一个ARIMA(p,0,q)过程

      拟合过程：

      第一步，确定适当的d值，即我们需要取差值的次数

• 平稳性检验——平稳即代表没有明显趋势且波动范围有限

        检验方法：

 

1. 时序图检验：根据平稳时间序列的均值和方差都为常数的性质，平稳序列的时序图显示该序列值始终在一个常数附近随机波动，而且波动的范围有界；如果有明显的趋势性或者周期性，那它通常不是平稳序列（直接把数据画在图上，看看他是不是平稳在某个值附近而且波动是有限的）

2. 自相关图检验：平稳序列具有短期相关性，这个性质表明对平稳序列而言通常只有近期的序列值对现时值得影响比较明显，间隔越远的过去值对现时值得影响越小。随着延迟期数k的增加，平稳序列的自相关系数会比较快的衰减趋向于零，并在零附近随机波动，而非平稳序列的自相关系数衰减的速度比较慢。（对于一个平稳序列而言，其k值较小时ACF图的值可以很大，但是随着k值变大，ACF图的值应该是迅速减小并衰减至0）

3. 单位根检验。指的是是否存在单位根，如果存在单位根，即为非平稳时间序列

                用的最多的就是扩展Dickey-Fuller（ADF）检验，创建的回归模型如下：

            

                其中，k代表模型中能容许的最大时间延迟数量，第一项来自于AR模型，最后一项来自于MA模型。

                ADF的零假设（原假设）是：当前时间序列是非平稳的——回归模型预测一个近似于0的系数

                当拒绝原假设时：当前时间序列是平稳的——回归模型预测的系数就会小于0

                R语言中调用adf.test()函数，这个函数会默认k值（因为拿到一个数据时候，不知道数据所建立的模型能容许的最大时间延迟数量是多少）等于不超过待检

                验时间序列长度的立方根的最大整数。返回的结果是一个p值，默认的置信度下，它的阈值是0.05，即小于0.05表明被检验的时间序列是平稳的，大于0.05

                表示被检验的时间序列是不平稳的

                附：单位根检验方法及方式：

                扩展Dickey-Fuller检验（ADF）——原假设为时间序列非平稳，p值小于0.05时时间序列被证明是平稳的，大于0.05为非平稳

                Philips-Perron检验（Philips-Perrontest）——原假设为时间序列非平稳，p值小于0.05时时间序列被证明是平稳的，大于0.05为非平稳

                Kwiatkowski-Phillips-Schmidt-Shin检验（KPSS）——原假设为时间序列平稳，p值小于0.05时时间序列被证明是非平稳的，大于0.05为平稳

      第二步，重复ARMA模型处理过程

3.ARCH模型

      当通过季节性变化和查分后，还不能用ARIMA模型解释时，这样的非平稳时间序列建模可以通过做出一个假设：假设数据非平稳的原因是该模型的方差会以一种可预见的方式随时间变化。基于这个假设，我们可以对方差随时间的变化建模为一个自回归过程（AR），这种模型也被称为自回归条件异方差（ARCH）。异方差性是描述常熟方差的同方差性的反义词。

      p阶ARCH模型的方程为：

      序列项的均值为0，其方差计算方式如下；为白噪声序列项（在这里我们假设白噪声过程的方差为1，均值为0，为了强调该过程是自回归过程；如果方差不是1，只会在结果中引入一个常数的乘数因子，但是不会改变模型的自回归本质）：

 

      可以看出ARCH模型在对于序列项在时间步骤t的方差是离它最近的过去的p个时间步骤所对应的方差的线性加权和。通过这样的过程，我们得到了一个可是别的p阶AR过程。

4.GARCH模型

      GARCH模型称作广义自回归条件异方差模型，等于一个ARCH模型增添了移动平均方差成分，ARCH（p）等价于  GARCH（p,0）

      GARCH（p，q）过程的一般形式如下：