导言
新的CNN网络的提出,提高了模型的学习能力但同时也带来了学习效率的降低的问题(主要体现在模型的存储问题和模型进行预测的速度问题),这使得模型的轻量化逐渐得到重视。轻量化模型设计主要思想在于设计更高效的“网络计算方式”(尤其针对卷积方式),从而不损失网络性能的前提下,减少网络计算的参数。本文主要介绍其中的一种——MobileNet[1](顾名思义,是能够在移动端使用的网络模型)。
深度可分离卷积
MobileNet实现模型轻量化的核心是depth-wise separable convolution,可翻译为深度可分离卷积,最早由Sifre在2014年提出[2]。直观上,此方法将CNN中传统卷积方法中的卷积(filtering)和求和(combining)这两个部分,拆分开来,从而极大地减小了网络计算的权值参数数量,提高了计算速度。
具体来讲,假设输入为\(D_F \times D_F \times M\)的特征图F(feature map),其中\(M\)表示输入特征的个数;若步长(stride)为1,且使用padding的话,则可知输出为\(D_F \times D_F \times N\)的特征图,设为G,其中N表示输出特征的个数。
对于传统卷积方法,需要使用\(N\)个$D_K \times D_K \times M $的卷积核,如图(a)所示:
这一卷积过程的数学表达式为:
可以看到计算每个\(G_n\)的时候, 都需要对所有的m进行计算并求和,而深度可分离卷积要做的,正是把(1)式中的m拿出来。
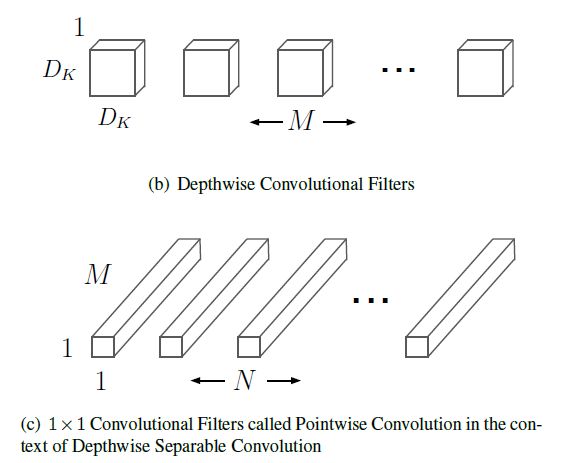
深度可分离卷积将传统的卷积和拆分成了卷积和求和两部分,其卷积核自然也由两部分构成,分别是:Depthwise Convolutional Filters和Pointwise Convolution Filter。
从图(b)(c)中,可以直观地看出,Depthwise Convolutional Filters包含了传统卷积核宽度(\(D_K\))和高度(\(D_k\))以及输入特征数(\(M\))这3个参数,Pointwise Convolution Filter包含了输出特征数(\(N\))这1个参数。原来的4个参数被拆分成3+1,对于计算有何影响呢?这时候,相应的计算式变成了:
(2)式中\(\hat{K}\)表示Depthwise Convolutional Filters卷积核,(3)式中\(\bar{K}\)表示Pointwise Convolution Filter卷积核。为了方便比较,我们把(2)代入(3),得到
比较(1)和(4),可以看出,通过这样的设计,我们成功地拿出了m,把求和号拆成了两部分。为了量化对计算速度提升的效果,我们可以计算前者与后者计算量的比值为:
可见,计算量的减少程度与\(D_K\)和\(N\)正相关,已知MobileNet中Depthwise Convolutional Filters卷积核为\(3\times3\),则随着N取遍大于1的正整数,该比值的变化范围为\((\frac{1}{9},\frac{11}{18}]\),对应的速度提升为\([1.64,9)\),且N越大,则速度提升越明显。
超参数
超参数的设计使得MobileNet能更好的适应不同用户对于速度和精度的需求。MobileNET主要有两个超参数:宽度乘子(Width Multiplier \(\alpha\))和分辨率乘子( Resolution Multiplier \(\rho\)),它们都与网络的卷积计算有着紧密的联系。宽度乘子\(\alpha\)作用于特征数量,对应到图(a)(b)(c)中为卷积核的数量,而分辨率乘子\(\rho\)作用于特征的尺寸,对应图中每个长方体的“横截面积”。更精确地,可以将考虑到超参数的卷积计算量表示如下:
在实际应用中,\(\alpha\)的取值一般为1,0.75,0.5和0.25,而\(\rho\)由选择的分辨率决定,默认的分辨率选择为224,192,160和128。
总结
MobileNet的提出是为了在保证网络性能的前提下,提高计算的速度,推动CNN在移动设备上的应用。这一轻量化模型的核心是利用深度可分离卷积将传统卷积中的卷积与求和两个步骤拆开,对应Depthwise Convolutional Filters和Pointwise Convolution Filter这两个卷积核。模型还提供了宽度乘子和分辨率乘子以平衡不同应用场景下对速度和精度的需求。
Howard, Andrew G., et al. "Mobilenets: Efficient convolutional neural networks for mobile vision applications." arXiv preprint arXiv:1704.04861 (2017). ↩︎
Sifre, L., and S. Mallat. Rigid-motion scattering for image classification, 2014. Diss. Ph. D. thesis, 2014. ↩︎