机器学习之聚类（Clustering，包含k-means,DBSCAN等算法）

聚类（Clustering）

前言 : 总结了许多聚类算法相关内容，并使用python自编程实现 kmeans, DBSCAN算法．待续包括：层次聚类算法，FCM算法，高斯混合聚类，还有性能度量．
参考书籍：<机器学习>，＜数据挖掘概念与技术＞

0. 基本内容

• 无监督学习
• 物以类聚：簇内相似度(intra-cluster similarity)和簇间相似度(inter-cluster similarity)
• 距离度量(distance measure)：闵可夫斯基距离
• 性能度量/有效性指标（validity index）：外部指标(external index)和内部指标(internal index)
• 外部指标：Jaccard系数(Jaccard coefficient, JC) ; FM指数(Fowlkes and Mallows Index, FMI) ; Rand指数(Rand Index, RI)
• 内部指标：DB指数(Davies-Bouldin Index, DBI) ; Dunn指数(Dunn Index, DI)

1. 关于主要思想（聚类任务）

聚类的基本思想比较简单，就是把看着像同类的数据划分到一块。

术语点说就是，将规则相似的数据聚集在一起，这些数据预先没有分类，即没有标签，最终将一些相似数据聚集到一块，产生了数据间的区分，但仍不能将其称作为每个具体的实际意义上的类，最终聚类的结果只是用于区分或者说是标注。所以聚类是一种非监督(no label)学习，解决的是标注问题。在聚类中被划分后每一块称作为一个簇（cluster）

可以根据一些示意图很好明白聚类的意图和思想

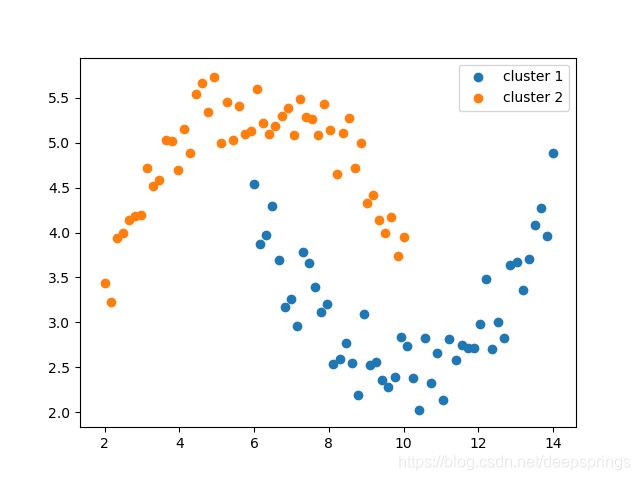
显而易见的是，相同的数据，使用不同的聚类规则会产生不同的结果。 聚类结果没有正误之分，只有对解决问题的适宜好坏之分。

对于聚类分析，有两点比较重要：

1. 能够处理任意形状的数据
2. 能够较好的处理噪声数据，离群点

对于聚类分析，有两个基本问题：

1. 如何选择聚类规则（算法）
2. 如何评价聚类结果（评测）

2. 关于聚类规则（聚类方法）

2.1 划分方法（partitioning method）

n 个对象集合划分为 k 簇，通常划分方法是基于距离，其主体思想类似与 LDA ，即使得划分后同簇对象间尽可能靠近，异簇对象间尽可能远离。如果要达到全局最优，要穷举遍历所有可能划分，计算量巨大，因此，通常使用逼近最优解的方法进行迭代（EM算法的意味渐浓）。这种方法通常适用于小规模球形数据结构的簇。

比较代表性的算法是 k-mens 算法

2.2 层次方法（hierarchical method）

2.3 基于密度（density-based method）

2.4 基于网格（grid-based method）

3. 聚类算法

3.1 k-means 算法

算法步骤

参考＜机器学习＞书本

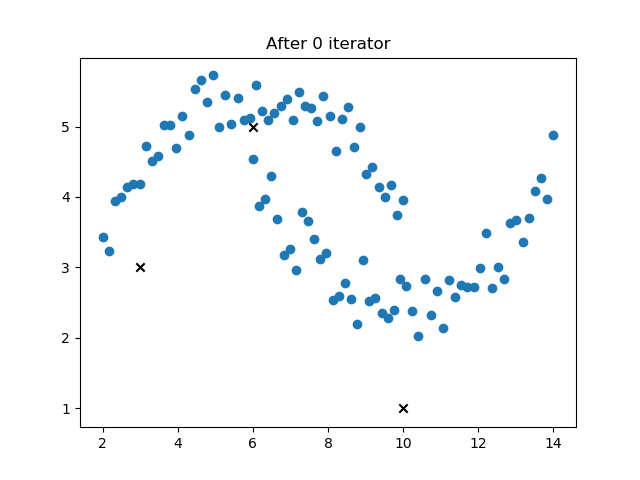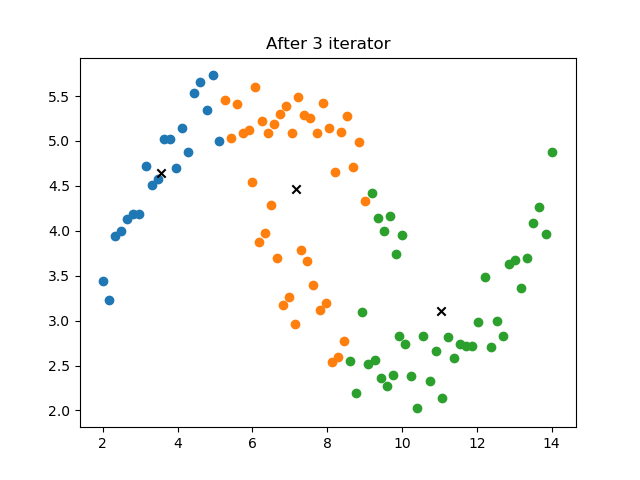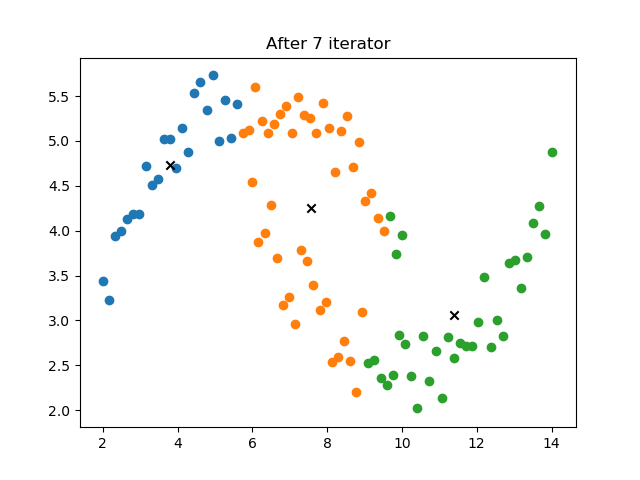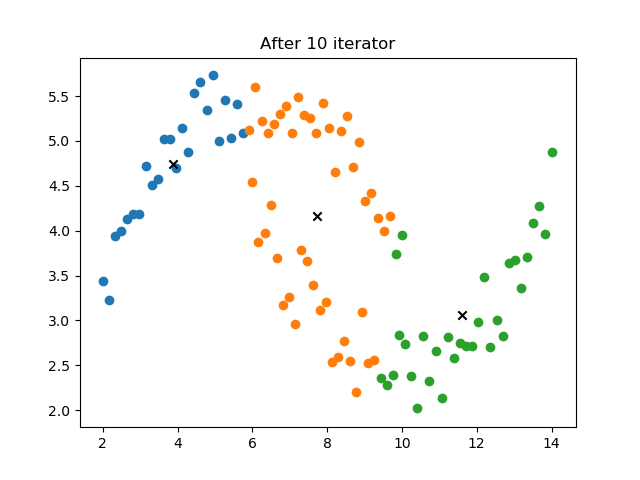
编程实现

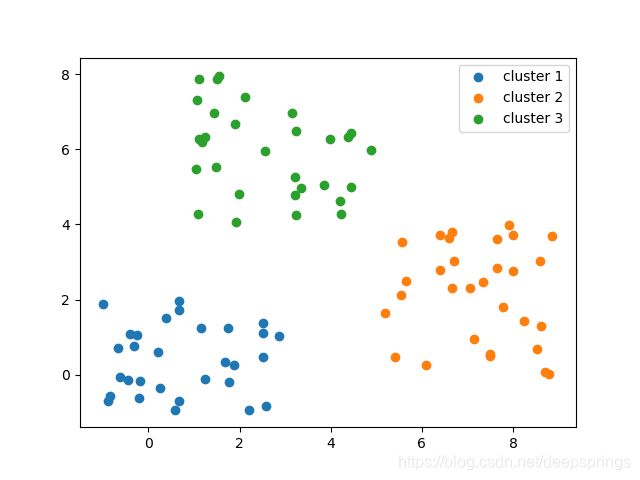
对上述第一个图中数据，实现 k-means 算法

# 实现输入原始数据data:list和初始聚类点数据kdata:list，可视化k-means算法过程

import numpy as np
import matplotlib.pyplot as plt
import imageio

class kmeans:
    
    def __init__(self, data, kdata):
        self.data = data    # 原始数据 
        self.kdata = kdata  # 聚类中心
        self.k = len(self.kdata)    # 聚类数
        self.it = 0 # 迭代次数
        self.clusterIni(0)

    def clusterIni(self, sig):
        self.cluster = {}   # 聚类
        for i in range(self.k):
            if i==0 and sig==0:
                self.cluster[i] = data
            else:
                self.cluster[i] = []

    # 迭代
    def iter(self):
        # 聚类
        self.clusterIni(1)
        for _i,i in enumerate(self.data):
            index = 0
            distance = 1.0
            for _j,j in enumerate(self.kdata):
                dis = (i[0]-j[0])**2 + (i[1]-j[1])**2
                if _j == 0:
                    distance = dis
                    index = 0
                elif dis <= distance:
                    distance = dis
                    index = _j
            self.cluster[index].append(i)

        # 计算新聚类中心
        count = 0
        for c in self.cluster:
            sx = 0
            sy = 0
            for d in self.cluster[c]:
                sx = sx + d[0]
                sy = sy + d[1]
            avgx = sx / len(self.cluster[c])
            avgy = sy / len(self.cluster[c])
            if avgx == self.kdata[c][0] and avgy == self.kdata[c][1]:
                count = count + 1
            else:
                self.kdata[c] = [avgx,avgy]
        self.it = self.it + 1
        if(count == len(self.kdata)):
            print("总迭代次数:%d"%(self.it-1))
            return 0
        else:
            return 1

    # 根据cluster可视化
    def plot(self, isSave = 0):
        # 显示簇
        for c in self.cluster:
            if(self.cluster[c] == []):
                continue
            x = np.array(self.cluster[c])[:,0]
            y = np.array(self.cluster[c])[:,1]
            plt.scatter(x, y)

        # 显示中心点
        mx = np.array(self.kdata)[:,0]
        my = np.array(self.kdata)[:,1]
        plt.scatter(mx, my, marker='x', color='black')

        plt.title("After %d iterator"%self.it)
        if isSave:
            plt.savefig("./cluster/%d.png"%self.it)
        plt.show()

if __name__ == '__main__':

    # 原始数据data
    data = []
    f = open('./clusterData.txt', 'r')
    for _d in f:
        dat = _d.rstrip().split(' ')
        data.append([float(dat[0]), float(dat[1])])
    f.close()

    # 初始聚类中心点kdata
    kdata = [[3,3],[2,2],[1,1]]

    obj = kmeans(data, kdata)
    # 迭代10次
    for i in range(10):
        obj.plot(1)
        b = obj.iter()
        # 或到稳定时结束
        if not b:
            print('迭代结束!')
            break
        #obj.plot(1)
    #obj.plot()

    # 合成成gif动画
    inp = []
    for i in range(obj.it):
        inp.append(imageio.imread('./cluster/%d.png'%i))
    outp = './cluster/cluster.gif'
    imageio.mimsave(outp, inp, duration=1)

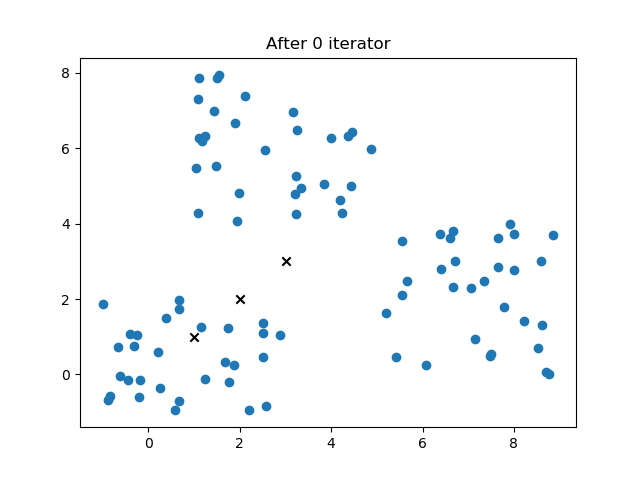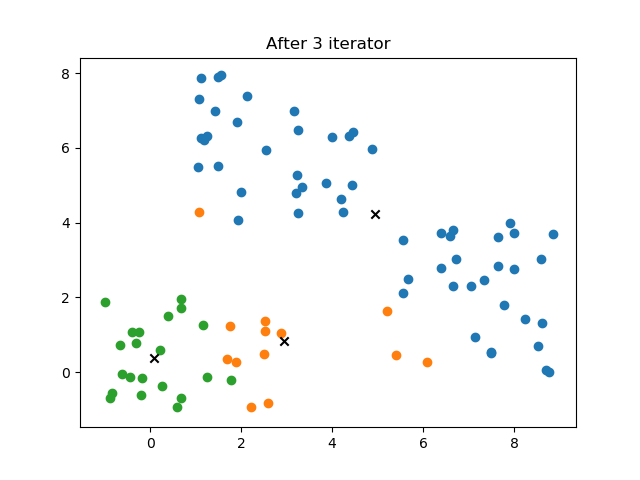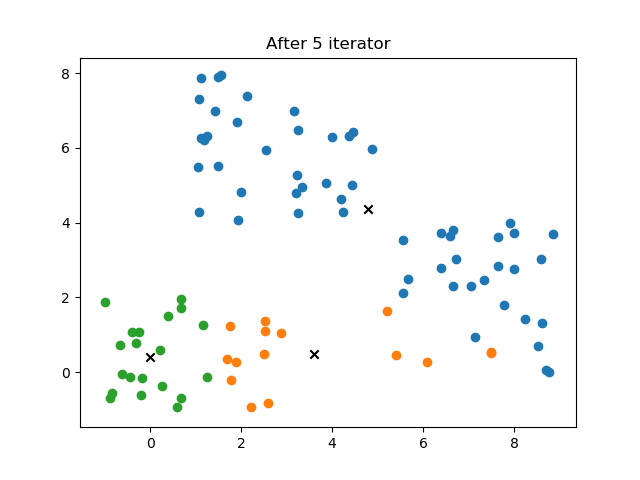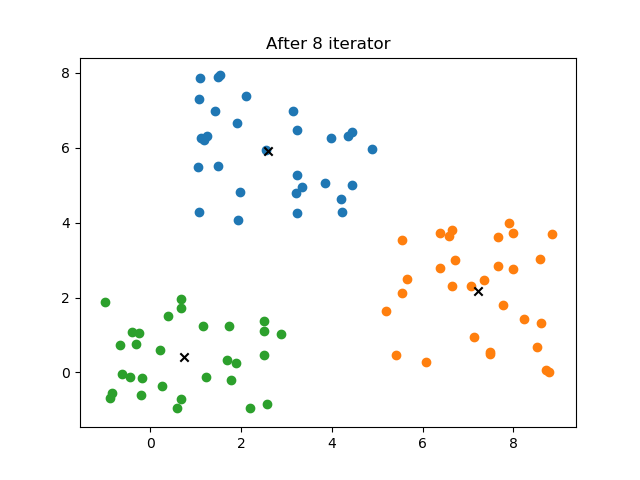
结果

图中 x 为中心点

心得

• 初始点选择一般是原始数据中存在的点，不然上面自编的k-means可能会出问题（不知官方包怎么样），因为可能出现分母为0情况

• 收敛速度确实很快，通常几步就可以得到最终结果

• 初始簇数的选择问题：k 的选择，即分簇的个数有时候难以预见

• 初始点的选择问题：初始中心点选择影响到最终结果，且最终是收敛于局部最优

• 适应的数据类型：只适用与球形数据，如上面的第二类数据就不适用

优缺点

• 思想简单，实现简单，收敛很快，时间复杂度 $O(t\cdot k\cdot n)$
• k 值选择很麻烦，且是局部收敛
• 因为是基于均值，所以i对噪点十分敏感
• 只适应于球形数据

实践中，为了得到好的结果，通常使用不同的初始簇，多次运行 k-means 算法

3.2 模糊Ｃ聚类(Fuzzy C-means cluster, FCM)

另见：https://blog.csdn.net/deepsprings/article/details/106820626

3.3 高斯混合聚类

3.4 具有噪声应用的基于密度的空间聚类（Density-Based Spatial Clustering of Applications with Noise, DBSCAN）

思想

该种聚类的思想也极其简单，其比较符合人眼判别结果。即，数据点密集的认为更可能是同一类。而为了表征这种解决问题的思路，使用了一些术语：

• $ϵ$ 邻域：与点距离不大于 $ϵ$ 的样本集。可以通过指定距离和符合条件的样本点集的数目，而这正是体现了密度的方面。这两个参数也是DBSCAN算法调参参数。
• 核心对象：某点临域内的样本点数大于指定值，那么该点就是核心对象。
• 密度直达：两个核心对象点临域相互包含对方。
• 密度可达：两个点相距较远，但可以通过多个密度直达点相连。
• 密度相连：密度可达点可以相连通，实现给定参数下同簇间的连通性。

在为一簇的情况下，结果有点类似于区域增长算法。但区域增长仅考虑了距离因素，而没有密度的因素。

算法步骤

参考＜机器学习＞书本

编程实现

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import queue

# 原始数据生成
def genData():
    theta = np.random.uniform(0, 2*np.pi, 250)
    r = np.random.uniform(4.5, 5.5, 250)
    x1 = r*np.sin(theta) + 5
    y1 = r*np.cos(theta) + 5
    x2 = np.random.uniform(1, 3, 20) + 1.5
    y2 = np.random.uniform(1, 3, 20) + 5
    x3 = np.random.uniform(1, 3, 20) + 4.5
    y3 = np.random.uniform(1, 2, 20) + 5
    x4 = np.random.uniform(4, 7, 30)
    y4 = np.random.uniform(2, 4, 30)
    x_ = np.random.uniform(0, 20, 50) - 5
    y_ = np.random.uniform(0, 20, 50) - 5
    x = np.hstack((x1, x2, x3, x4, x_)) + 5
    y = np.hstack((y1, y2, y3, y4, y_)) + 5
    plt.scatter(x, y)
    plt.xlim((0, 15))
    plt.xlim((0, 15))
    plt.axis('equal')
    plt.show()
    dataF = pd.DataFrame({'x':x, 'y':y})
    dataF.to_csv('./data.csv')

# 读取原始数据集
def getData():
    data_0 = pd.read_csv('./data.csv')
    dataA = np.array(data_0)[:,1:]
    dataL = dataA.tolist()
    # plt.scatter(dataA[:,0], dataA[:,1])
    # plt.show()
    return dataL


# 自编程实现
class DBSCAN:
    def __init__(self, data, eps, min_samples):
        self.data = data # 原始数据
        self.eps = eps
        self.minP = min_samples - 1
        self.core = []
        self.k = 0
        self.cluster = {} # 聚类结果
    
    # 得到某点 d<=r 的邻域点, data数据集，isCont是否包含自身
    def getN(self, point, r, isCont = 0):
        data = self.data[:]
        data.remove(point)
        Nei = []
        for i in data:
            dis = (i[0]-point[0])**2 + (i[1]-point[1])**2
            if dis <= r**2:
                Nei.append(i)
        if isCont:
            Nei.append(point)
        return Nei
    
    # 获取两点集的交集
    def intersection(self, ptL1, ptL2):
        inters = []
        for i in ptL1:
            if i in ptL2:
                inters.append(i)
        return inters
        
    # 获取核心对象, isPlot是否可视化
    def getCore(self, isPlot = 0):
        data = self.data[:]
        for i in data:
            temp = self.getN(i, self.eps)
            if len(temp) >= self.minP:
                self.core.append(i)
        if isPlot:
            x = np.array(self.core)[:,0]
            y = np.array(self.core)[:,1]
            plt.scatter(np.array(self.data)[:,0], np.array(self.data)[:,1])
            plt.scatter(x, y)
            plt.legend(('rawPoint','corePoint'))
            plt.show()
    
    # 算法迭代
    def dbscan(self):
        q = queue.Queue()
        core = self.core[:]
        Data = self.data[:]
        while len(core) != 0:
            dat = Data[:]
            q.put(core[0])
            Data.remove(core[0])
            while not q.empty():
                pt = q.get()
                Nei = self.getN(pt, self.eps)
                if len(Nei) >= self.minP:
                    delta = self.intersection(Nei, Data)
                    for i in delta:
                        q.put(i)
                        Data.remove(i)
            self.k = self.k + 1
            self.cluster[self.k] = dat[:]
            for j in Data:
                self.cluster[self.k].remove(j)
            for k in self.cluster[self.k]:
                try:
                    core.remove(k)
                except:
                    continue
        self.cluster[0] = Data   # key = 0,对应于噪点
    
    def plot(self):
        for i in self.cluster:
            x = np.array(self.cluster[i])[:,0]
            y = np.array(self.cluster[i])[:,1]
            plt.scatter(x, y)
        plt.show()

# 测试
if __name__ == '__main__':
    genData()
    dataL = getData()
    db = DBSCAN(dataL, 0.8, 5)
    db.getCore()
    db.dbscan()
    db.plot()


    # 使用官方库
    import sklearn.cluster as skc
    dataA = np.array(dataL)
    y_pred = skc.DBSCAN(eps = 0.8, min_samples = 5).fit_predict(dataA)
    plt.scatter(dataA[:, 0], dataA[:, 1], c=y_pred)
    plt.show()

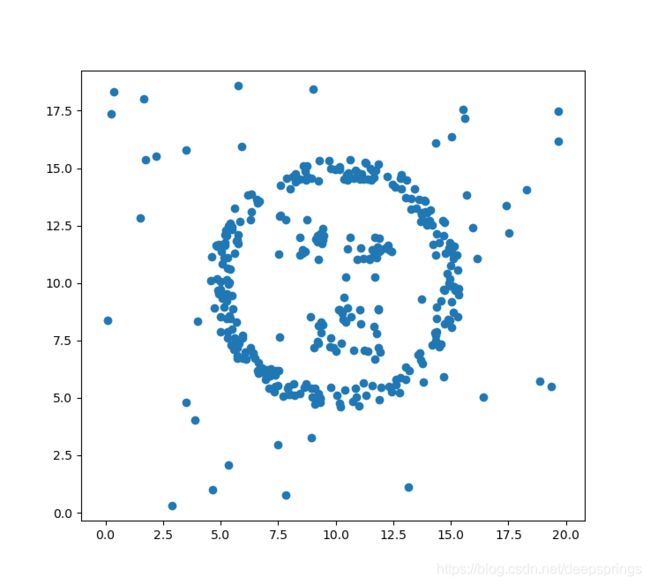
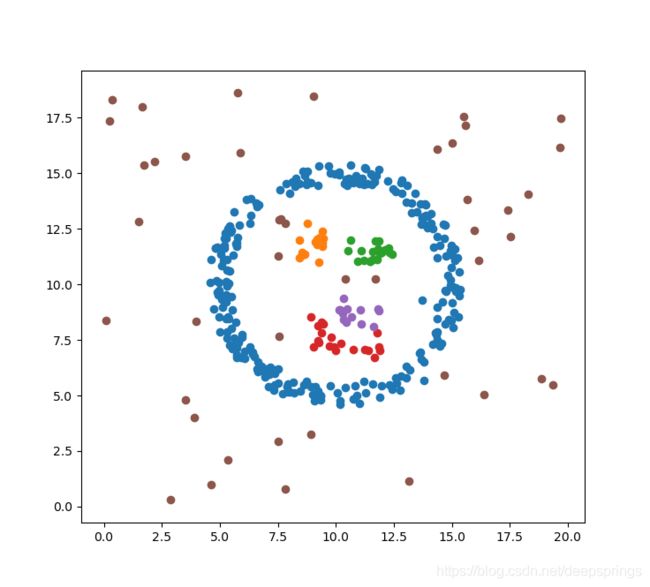
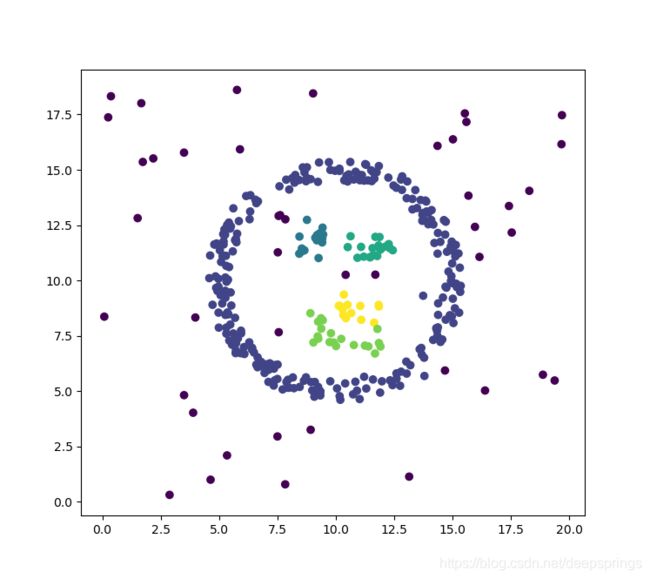
结果

原始数据

自编代码

官方库

心得

• 可以适用于各种形状，可以处理噪点离群点，不必烦恼ｋ-means 的ｋ值
• 参数 $ϵ$ 和 $minPts$ 选择尝试也并不简单

3.5 层次聚类

4. 关于结果评测（性能度量）

一种显而易见的方法是类似与 LDA 算法中同类间距分布的度量，即通过查看簇内数据散布情况，
$$\begin{gathered} J_e=\sum _{i=1}^n\sum _{x\in D_i}||x-m_i|{|}^2 \\ here,m_i=\frac{1}{n_i}\sum _{x\in D_i}x \end{gathered}$$