算法解剖系列-Otsu二值化原理及实现

基本原理

• Otsu是以统计决策为基础的；

• Otsu方法在类间方差最大的情况下获取最佳阈值，达到最佳分割效果；（即，在目标与背景之间差别最大时获取的阈值）

• Otsu方法是以图像的相对直方图（归一化直方图）为基础对一维阵列进行计算的；

推导大致过程：

对一幅大小为 M×N 的数字图像：

令 L 表示灰度级数；

ni 表示灰度级为 i 的像素数，则图像中像素总数 MN=n1+n2+n3+⋅⋅⋅+nL；

pi=ni/MN,pi 为相对直方图，即灰度级为 i 出现的概率。则 ∑Li=1pi=1 ；

设阈值 T(k)=k,1<k<L可以将图像分为C1和C2两类，灰度值范围分别为[1,k]和[k+1,L] 。

• 则被分到 C1和C2 的概率分别为：
  P1(k)=∑ki=1pi(1)
  P2(k)=∑Li=k+1pi=1−P1(k)(2)

• 则被分到 C1和C2 像素的灰度均值分别为：
  m1(k)=∑ki=1iP(i/C1)=∑ki=1iP(C1/i)P(i)/P(C1)=1P1(k)∑ki=1ipi(3)
  m2(k)=∑Li=k+1iP(i/C2)=1P2(k)∑Li=k+1ipi(4)

• 直至 k 级的累加均值：
  m(k)=∑ki=1ipi(5)

• 图像的灰度均值（即全局均值）：
  mG=∑Li=1ipi(6)

由 （3）和（4） 得：
P1m1+P2m2=mG(7)
类间方差：
σ2B=P1(m1−mG)2+P2(m2−mG)2(8)
将 （7）中的mG代入（8）中，以及由P1+P2=1 得：

σ2B=P1P2(m1−m2)2(9)

最后由 (3)(5)得m1=1P1m，由（7）得m2=mG−P1mP2,以及由P1+P2=1得 ：

σ2B=(mGP1−m)2P1(P1−1)

所以要获取类间方差，只需要计算全局均值 mG、k级的累加均值m和累加概率P1 。

设 σ2G代表全局方差，η 表示可分性度量，表示可分割性：

σ2G=∑i=1L(i−mG)2pi

η=σ2Bσ2G

最终的要计算的是：

σ2B（k）=(mGP1(k)−m(k))2P1(k)(P1(k)−1)(10)

η(k∗)=σ2B(k∗)σ2G(11)

k∗是最佳阈值，即σ2B（k）为最大值的k值。

算法基本步骤

---

1. 计算输入图像的相对直方图:根据 pi=ni/MN ；

2. 计算像素被分到 C1累计和P1(k),根据上式(1) ；

3. 计算累计均值 m(k),根据上式(5) ；

4. 计算全局灰度均值 mG，根据上式(6) ；

5. 计算类间方差 σ2B(k)，根据上式(10) ；

6. 获取最大的 σ2B(k)中的k 值，即为最佳阈值；

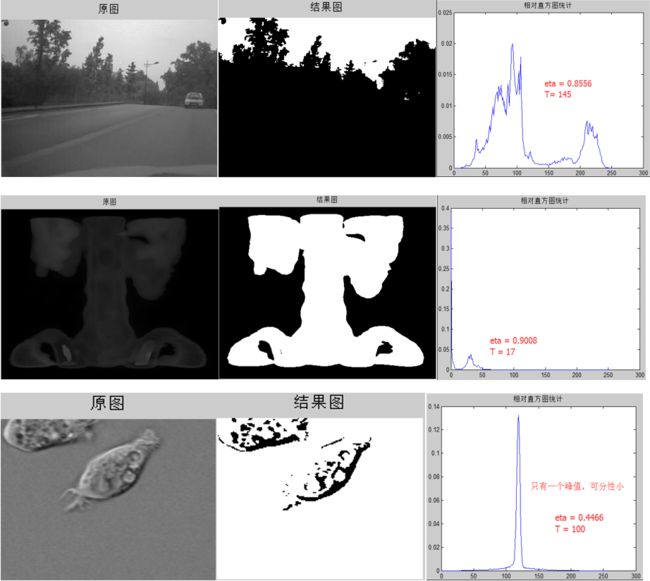
7. 计算可分性度量 η∗，根据上式(11) 。

---

算法实现

matlab 代码

close all;
clear all;
clc;

input = imread('R.png');%读图
input = rgb2gray(input);%灰度转换

L = 256;%给定灰度级
[ni, li] = imhist(input,L);  %ni-各灰度等级出现的次数；li-对应的各灰度等级
% figure,plot(xi,ni);%显示绝对直方图统计
% title('绝对直方图统计')

[M,N] = size(input);%获取图像大小
MN = M*N;%像素点总数

%%Step1 计算归一化直方图

pi = ni/MN;  %pi-统计各灰度级出现的概率
figure,plot(li,pi);%显示相对直方图统计
title('相对直方图统计')

%%Step2  计算像素被分到C1中的概率P1(k)

sum = 0;%用来存储各灰度级概率和
P1 = zeros(L,1);%用来存储累积概率和
for k = 1:L
    sum = sum +pi(k,1);
    P1(k,1) = sum;%累加概率
end

%%Step3  计算像素至K级的累积均值m(k)

sum1 = 0;%用来存储灰度均值
m = zeros(L,1);%用来存储累计均值
for k = 1:L
    sum1 = sum1+k*pi(k,1);
    m(k,1) = sum1;%累积均值
end

%%Step4  计算全局灰度均值mg

mg = sum1;

%%Step5 计算类间方差sigmaB2 
sigmaB2 = zeros(L,1);
for k = 1:L
    if(P1(k,1) == 0)
        sigmaB2(k,1) = 0;  %为了防止出现NaN
    else
        sigmaB2(k,1) = ((mg*P1(k,1)-m(k,1))^2)/(P1(k,1)*(1-P1(k,1)));
    end
end

%%Step6 得到最大类间方差以及阈值

[MsigmaB2,T] = max(sigmaB2);%获取最大类间方差MsigmaB2，以及所在位置（即阈值）
output = zeros(M,N);%定义二值化输出图像
for i = 1:M
    for j = 1:N
        if input(i,j)>T
            output(i,j) = 1;
        else
            output(i,j)=0;
        end
    end
end
figure,imshow(output);%显示结果

%%Step7 可分性度量eta

sigmaG2 = 0;%全局方差
for k = 1:L
    sigmaG2 = sigmaG2+(k-mg)^2*pi(k,1);
end
eta = MsigmaB2/sigmaG2;

效果图