顺时针打印矩阵(编程题讲解)

   《剑指offer》 编程题讲解。

题目描述

   输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字，例如，如果输入如下4 X 4矩阵： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10。

题目分析

   最基础的解法就是什么技巧都不谈，也不考虑数据结构和算法的相关东西，无非就是考虑在编写代码的时候循环的边界条件，通常好的边界条件设置，可以减少循环判断的次数，甚至减少循环的执行次数。
   大致分析一下，首先可以把任务分解成循环打印每一个圈的数据，每一个圈有四条边，然后打印多个圈就解决了这道题。编写代码的时候要注意测试用例的特殊情况，因为打印圈之后可能最后剩下的元素不构成一个圈了。这就又包括三种情况，四条边退化为一行，四条边退化为一列，四条边退化为一个元素，四条边退化为一个元素的可以归到前两种情况中处理。
   《剑指offer》 书本里的处理是将三种情况放在最后判断，感兴趣的自行查阅相关资料。而我独立完成的做法略微有点不同，不过思路是类似的。我将判断条件纳入了循环之内，能够稍微的精简代码。每一圈仍然从$(i,i)$的位置开始顺时针打印，分四个子区域，两个行平行，两个列平行，这样在写代码的时候就不容易混乱。区域划分如下图，假设从$(1,1)$的位置开始打印。

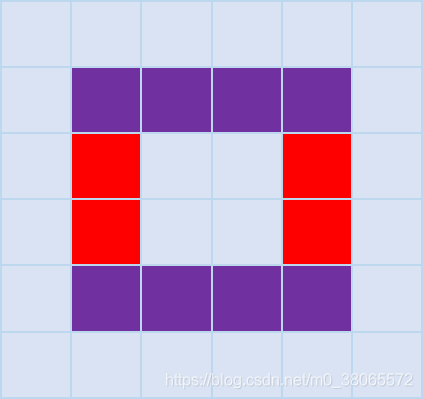
  在转圈的时候我让循环多执行一次，这样就把最后不足一个整圈的情况也纳入了循环中考虑。我把自己的python代码贴出来供大家参考。有什么疑问欢迎在下面留言讨论。

python代码

def printMatrix(self, matrix):
    res = []
    n = len(matrix)
    m = len(matrix[0])
    for o in range((min(m, n) + 1) // 1):# 这里加1，在行数/列数是奇数的时候让代码多执行一次
        res.extend([matrix[o][i] for i in range(o, m - o)])
        res.extend([matrix[j][m - 1 - o] for j in range(o + 1, n - o - 1)])
        if n - 1 - o > o:
            res.extend([matrix[n - 1 - o][m - i - 1] for i in range(o, m - o)])
        if m - 1 - o > o:
            res.extend([matrix[n - j - 1][o] for j in range(o + 1, n - o - 1)])
    return res

  如果大家想进一步减少判断的次数，可以把循环中的两个判断拿出来放在循环外面。因为代码中每一个子循环严格的条件控制，即便外层循环多执行几次也不影响结果。

使用python矩阵的旋转

  如果有一个矩阵，根据数学关系我们能知道，矩阵的旋转可以通过转置和翻转来实现，我们先来看以下的操作。
$${\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]}^T=\left[\begin{array}{cc}1& 3\\ 2& 4\end{array}\right]$$
$$reverse\left(\left[\begin{array}{cc}1& 3\\ 2& 4\end{array}\right]\right)=\left[\begin{array}{cc}2& 4\\ 1& 3\end{array}\right]$$
  可以证明矩阵的逆时针旋转就是先对矩阵转置，然后翻转。
$$reverse\left(\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]\right)=\left[\begin{array}{cc}3& 4\\ 1& 2\end{array}\right]$$
$${\left[\begin{array}{cc}3& 4\\ 1& 2\end{array}\right]}^T=\left[\begin{array}{cc}3& 1\\ 4& 2\end{array}\right]$$
  可以证明矩阵的顺时针旋转就是先对矩阵翻转，然后转置。
  我们可以很快的写出矩阵的转置代码，就是对矩阵中$(i,j)$和$(j,i)$不停的对换即可。代码如下

矩阵的转置代码

def transpose(matrix):
    for i in range(len(matrix)):
        for j in range(i + 1, len(matrix)):
            matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

  当然这是方阵的类型，如果不是方阵就得开辟空间，然后一列一列的加入。我们直接给出python的简化代码。

操作	代码
转置	matrix[:]=map(list,zip(*matrix))
顺时针旋转	matrix[:] = map(list,zip(*matrix[::-1]))
逆时针旋转	matrix =list(map(list,zip(*matrix)))[::-1]

  熟悉了以上操作，这道题的代码就可以简单很多，我们可以考虑拿出矩阵的第0行加入到打印的队列里，同时把矩阵中的第0行删除，这个时候需要打印右边的一列，可以把矩阵逆时针旋转，最后一列就变成了第一行，然后重复。这样就用矩阵的转圈代替了打印变量的转圈。算法难想，但是代码简单。

python旋转矩阵解法代码

def printMatrix(matrix):
    matrix = matrix.copy()  # 拷贝一份，防止修改改变原来的数据
    result = []
    while (matrix):
        result += matrix.pop(0)
        matrix = list(map(list, zip(*matrix)))[::-1]

    return result

  很显然第一种方式的实现要比第二种方式实现起来复杂一些，但是效率很高，即便是换做其他语言，改动也不是很大，但是循环复杂，循环条件多，容易出错，第二种方式思路复杂，想出来需要有一定的技巧，而且要有编码基础，但是运行效率低，需要对不停地开辟空间来拷贝旋转的数组，当问题的规模非常大的时候，第二种方式的开销将是巨大的。