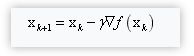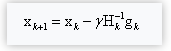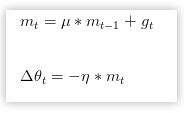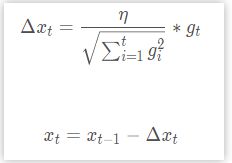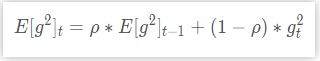6种机器学习中的优化算法：SGD,牛顿法,SGD-M,AdaGrad,AdaDelta,Adam

本文一共介绍6种机器学习中的优化算法：

1.梯度下降算法（SGD）

2.牛顿法

3.SGD-M

4.AdaGrad

5.AdaDelta

6.Adam

 

1.梯度下降算法（SGD）

用梯度下降算法最小化目标函数f(x)，梯度下降算法沿着梯度向量的反方向进行迭代以得到函数的极值点。参数迭代公式：

其中，γ为学习率，参数初始值为x0,即起始位置。

设置迭代停止条件：

1.达到最大迭代次数

2.梯度小于设定值

 

 

2.牛顿法

用牛顿法最小化目标函数f（x）

牛顿发直接使用驻点处导数为0得出参数迭公式：

其中，γ为学习率，参数初始值为x0,即起始位置。

用到了梯度的一阶导数gk，和二阶导数Hk。

停止迭代条件：

1. 达到最大迭代次数

2. 梯度小于设定值

缺点：求解Hessian矩阵的逆矩阵或者求解线性方程组计算量大，需要耗费大量的时间。

求的点是极小值点并不一定是最小值点。

 

3.SGD-M

momentum是模拟物理里动量的概念，更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向，可以在一定程度上增加稳定性，从而学习更快，并且还有摆脱局部最优的能力。

其中，u为动量因子，该算法的特点:

1. 下降初期时，使用上一次参数更新，下降方向一致，乘上较大的够进行很好的加速。

2. 下降中后期时，在局部最小值来回震荡的时候，得更新幅度增大，跳出陷阱。

3. 在梯度改变方向的时候，够减少更新 总而言之，momentum项能够在相关方向加速SGD，抑制振荡，从而加快收敛。

 

4.AdaGrad

AdaGrad为自适应梯度，是梯度下降算法变体，根据历史梯度值来调整学习率，参数迭代公式：

其中gt 表示当前迭代次数的梯度值。

该算法的特点：

• 优点：学习率将随着梯度的倒数增长，也就是说较大梯度具有较小的学习率，而较小的梯度具有较大的学习率，可以解决普通的sgd方法中学习率一直不变的问题

• 缺点：还是需要自己手动指定初始学习率，而且由于分母中对历史梯度一直累加，学习率将逐渐下降至0，并且如果初始梯度很大的话，会导致整个训练过程的学习率一直很小，从而导致学习时间变长。

 

5.AdaDelta

AdaDelta是对AdaGrad的改进，在一个窗口中对梯度进行求和，而不是对梯度一直累加。将累计梯度信息从全部历史梯度变为当前时间向前的一个窗口期内的累积：

相当于历史梯度信息的累计乘上一个衰减系数ρ，然后用(1−ρ) 作为当前梯度的平方加权系数相加。

最后的公式如下：

其中ϵ 是为了防止分母为0而加上的一个极小值。这种更新方法解决了对历史梯度一直累加而导致学习率一直下降的问题，当时还是需要自己选择初始的学习率。

 

6.Adam

Adam(Adaptive Moment Estimation)是一种不同参数自适应不同学习速率方法，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳。

mt,ntmt,nt分别是梯度的带权平均和带权有偏方差，初始为0向量，Adam的作者发现他们倾向于0向量(接近于0向量)，特别是在衰减因子(衰减率)μ,ν接近于1时,所以要进行偏差修正，m^t 和n^t是对mt nt,的校正。论文推荐参数：μ=0.9,ν=0.999,ϵ=10-8 。

 

该算法的特点：

1. 对于稀疏数据，尽量使用学习率可自适应的优化方法，不用手动调节，而且最好采用默认值。

2. SGD通常训练时间更长，但是在好的初始化和学习率调度方案的情况下，结果更可靠。

3. 如果在意更快的收敛，并且需要训练较深较复杂的网络时，推荐使用学习率自适应的优化方法。

 

 

参考：

http://blog.csdn.net/heyongluoyao8/article/details/52478715

https://zhuanlan.zhihu.com/p/22252270

http://blog.csdn.net/golden1314521/article/details/46225289

https://arxiv.org/pdf/1706.10207.pdf

 

推荐阅读，最新比较热门由中国小哥提出的AdaBound算法

比Adam,SGD更优秀的AdaBound实验对比代码

喜欢欢迎收藏，转载，分享！