NOIP2013车站分级
NOIP2013车站分级
题目描述 Description
一条单向的铁路线上,依次有编号为1, 2, …, n的n个火车站。每个火车站都有一个级别,最低为1级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站x,则始发站、终点站之间所有级别大于等于火车站x的都必须停靠。(注意:起始站和终点站自然也算作事先已知需要停靠的站点)
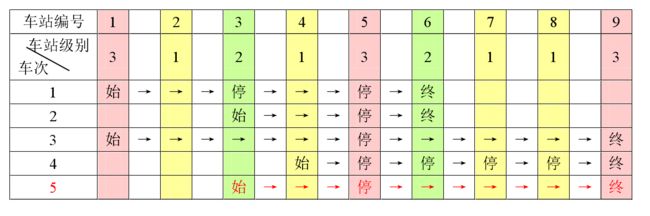
例如,下表是5趟车次的运行情况。其中,前4趟车次均满足要求,而第5趟车次由于停靠了3号火车站(2级)却未停靠途经的6号火车站(亦为2级)而不满足要求。
输入描述 Input Description
第一行包含2个正整数n, m,用一个空格隔开。
第i+1行 (1<=i<=m) 中,首先是一个正整数 si(2<=si<=n) ,表示第i趟车次有 si 个停靠站;接下来有 si 个正整数,表示所有停靠站的编号,从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。
输出描述 Output Description
输出只有一行,包含一个正整数,即n个火车站最少划分的级别数。
样例输入 Sample Input
[Sample 1]
9 2
4 1 3 5 6
3 3 5 6
[Sample 2]
9 3
4 1 3 5 6
3 3 5 6
3 1 5 9
样例输出 Sample Output
[Sample 1]
2
[Sample 2]
3
数据范围及提示 Data Size & Hint
对于20%的数据,1 ≤ n, m ≤ 10;
对于50%的数据,1 ≤ n, m ≤ 100;
对于100%的数据,1 ≤ n, m ≤ 1000。
Solution:
估计看到这道题一点都没往图论上想的也就是我了吧。还得多做点题啊…
既然明确了方向那么这题也就不算难了。首先考虑50%的数据,我们知道对于每一列车,它经过的站点中停了的站点的等级肯定比没停的站点高。因此对于每一辆车,我们可以把它经过的每一个没停的站点向每一个停了的站点建一条边。然后我们会得到一张图,在这张图上找最长的一条路段即可。这个工作可以用拓扑排序完成。复杂度 O(n3)
#includeint main(){
int n,m;
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d",&s[i][0]);
for(int j=1;j<=s[i][0];j++)
scanf("%d",&s[i][j]);
}
for(int i=1;i<=m;i++){
for(int j=1;j<=s[i][0];j++)
mark[s[i][j]]=true;
for(int j=s[i][1];j<=s[i][s[i][0]];j++){
if(mark[j])continue;
for(int k=1;k<=s[i][0];k++)
d[j][s[i][k]]=true;
}
for(int j=1;j<=s[i][0];j++)
mark[s[i][j]]=false;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(d[i][j])degree[j]++;
for(int i=1;i<=n;i++)
if(degree[i]==0){
Q.push(i);
dp[i]=1;
}
while(!Q.empty()){
int top=Q.front();
Q.pop();
for(int i=1;i<=n;i++){
if(!d[top][i])continue;
degree[i]--;
check(dp[i],dp[top]+1);
if(degree[i]==0)Q.push(i);
}
}
int ans=0;
for(int i=1;i<=n;i++)
check(ans,dp[i]);
printf("%d\n",ans);
} 众所周知,历年普及组数据是水的不行,所以这份代码也能过。
然后考虑正解,显然对于点考虑是无法再优化了,因此我们考虑车。我们定义一辆车的等级就是它经过站点的最小等级。我们考虑如何判定两辆车的等级大小。
对于两辆车,它们如果没有交点,那么它们的等级没有关系。
两辆车相交区间(都有停的区间)中,如果一辆车停的车辆多,那么它的等级低。
于是我们就建立了两辆车之间的大小关系,同样的,应用拓扑排序就可以找到这个最大的等级。复杂度 O(n2)
最后,还有一点要注意,因为我们处理的是车,而最后要求的是点。如果对于一辆等级为1的车,它经过的站点中如果有一个站点一辆车都没有停靠,那么最后的答案就要加1。
#includeint main(){
int n,m;
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d",&s[i][0]);
for(int j=1;j<=s[i][0];j++){
scanf("%d",&s[i][j]);
mark[s[i][j]]=true;
}
for(int j=1,t=1;t<=n;t++){
sum[i][t]=sum[i][t-1];
if(s[i][j]==t){
if(j0])j++;
sum[i][t]++;
}
}
}
for(int i=1;i<=m;i++)
for(int j=i+1;j<=m;j++){
int a=i,b=j;
if(s[j][1]1])swap(a,b);
int st=max(s[a][1],s[b][1]),ed=min(s[a][s[a][0]],s[b][s[b][0]]);
int s1=sum[a][ed]-sum[a][st-1];
int s2=sum[b][ed]-sum[b][st-1];
if(s1>s2)d[a][b]=true;
else if(s1true;
}
for(int i=1;i<=m;i++)
for(int j=1;j<=m;j++)
if(d[i][j])degree[j]++;
for(int i=1;i<=m;i++)
if(degree[i]==0){
Q.push(i);
dp[i]=1;
}
while(!Q.empty()){
int top=Q.front();
Q.pop();
for(int i=1;i<=m;i++){
if(!d[top][i])continue;
degree[i]--;
check(dp[i],dp[top]+1);
if(degree[i]==0)Q.push(i);
}
}
int f=0;
for(int i=1;i<=m;i++){
if(dp[i]!=1)continue;
for(int j=s[i][1];j<=s[i][s[i][0]];j++)
if(mark[j]==0){
f=1;
break;
}
if(f)break;
}
int ans=0;
for(int i=1;i<=m;i++)
check(ans,dp[i]);
printf("%d\n",ans+f);
}